Метод контурных токов
 Скачать 481.51 Kb. Скачать 481.51 Kb.
|
Метод контурных токовРассмотренный выше метод расчета электрических цепей на основе законов Кирхгофа при анализе больших и разветвленных цепей приводит к неоправданно трудоемким расчетам, поэтому редко применяется. Более широко используется метод контурных токов, позволяющий значительно сократить количество уравнений. Метод контурных токов — метод расчёта электрических цепей, при котором за неизвестные принимаются токи в контурах, образованных некоторым условным делением электрической цепи. Метод контурных токов основан на допущении, что в каждом из Nк независимых контуров схемы циркулирует некоторый виртуальный контурный ток. Если некоторая ветвь принадлежит только одному контуру, реальный ток в нём равен контурному. Если же ветвь принадлежит нескольким контурам, ток в нём равен сумме соответствующих контурных токов (с учётом направления обхода контуров). Поскольку независимые контура покрывают собой всю схему (т.е. любая ветвь принадлежит хотя бы одному контуру), то ток в любой ветви можно выразить через контурные токи, и контурные токи составляют полную систему токов. Т.е.изначально вместо токов в ветвях электрической цепи определяются контурные токи при помощи второго закона Кирхгофа. Таким образом, количество требуемых уравнений будет равняться числу независимых контуров. Наиболее простым и наглядным методом построения системы независимых контуров является построение планарного графа схемы, то есть размещение ветвей и узлов цепи на плоскости без взаимных пересечений . Планарный граф разбивает плоскость на К ограниченных областей. Можно показать, что замкнутые части, ограничивающие эти области, являются системой независимых контуров для рассматриваемой схемы. Метод планарного графа предпочтителен при ручном расчёте схем. В случае, если схему невозможно изобразить в виде планарного графа, а также в случае компьютерного построения системы контуров применение этого метода может оказаться невозможным. В качестве примера рассчитаем цепь изображённую на рисунке ниже 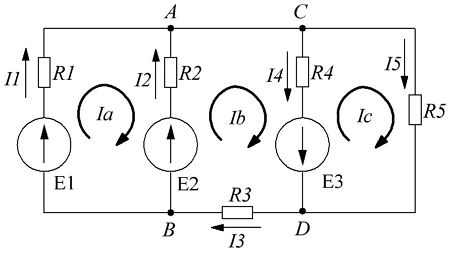 Расчет цепи методом контурных токов. Если бы мы вели расчёт цепи по методу законов Ома и Кирхгофа, то необходимо было бы решить систему из пяти уравнений. Для расчёта по методу контурных токов необходимо всего три уравнения.Задаём направления токов ветей,которые требуется определить В начале расчёта выделяют независимые контуры, в нашем случае это: E1R1R2E2, E2R2R4E3R3 и E3R4R5. Затем контурам присваивают произвольно направленный контурный ток, который имеет одинаковое направление для всех участков выбранного контура, в нашем случае для первого контура контурный ток будет Ia, для второго – Ib, для третьего – Ic. Как видно из рисунка некоторые контурные токи соответствуют токам в ветвях Остальные же токи можно найти как разность двух контурных токов В результате выбора контурных токов можно составить систему уравнений по второму закону Кирхгофа  Рассчитаем схему, изображённую на рисунке выше со следующими параметрами E1 = E3 = 100 B, E2 = 50 B, R1 = R2 = 10 Ом, R3 = R4 = R5 = 20 Ом. Запишем систему уравнений 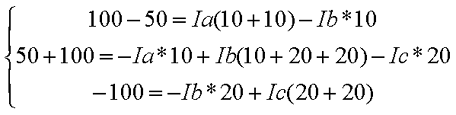 В результате решения системы получим Ia = I1 = 4,286 А, Ib = I3 = 3,571 А, Ic = I5 = -0,714 А, I2 = -0,715 А, I4 = 4,285 А. Так же как и в предыдущем случае если токи получаются отрицательными, значит действительное направление противоположно принятому. Таким образом, токи I2 и I5 имеют направление противоположное изображённым на рисунке. Метод наложенияВ любой линейной системе реакция на сумму воздействий равна сумме реакций на каждое воздействие в отдельности. В цепях воздействие – это источники напряжения и источники тока, а реакция – это токи ветвей и напряжения между какими - то точками схемы. Поэтому любой ток или напряжение в линейной цепи с несколькими источниками равен сумме частичных значений тока или напряжения, вызванных действием каждого источника в отдельности. Свойство наложения (суперпозиции) справедливо только для токов и напряжений. Для мощностей этот принцип не выполняется, так как мощности элементов рассчитываются по нелинейным уравнениям. Метод наложения основан на принципе наложения. Примерный порядок расчета 1. Выбирают положительное направление токов ветвей и нумеруют все узлы схемы. 2. Исходную схему представляют в виде нескольких подсхем. В каждой подсхеме оставляют один или несколько автономных источников в общем случае одной и той же частоты, что определяется простотой расчета. Остальные автономные источники заменяют их внутренним сопротивлением. Все автономные источники должны войти в подсхемы, но только один раз. 3. Рассчитывают частичный режим в каждой подсхеме любым рациональным методом. 4. Режим в исходной схеме определяют как алгебраическую сумму частичных режимов. Если необходимо, то рассчитывают мощности. 5. Проверку правильности расчета режима цепи проводят по балансу мощностей или законам Кирхгофа. Примечание: если в схеме есть управляемые (зависимые) источники, то их сохраняют во всех подсхемах. Теорема об эквивалентном генераторе Метод эквивалентного генератораПри решении задач желательно упростить описание схемы. Один из приемов, позволяющий это сделать состоит в том, что часть схемы с двумя зажимами рассматривают как двухполюсник с описанными свойствами, не интересуясь процессами происходящими внутри него. Двухполюсники – это любая часть схемы, рассматриваемая относительно двух зажимов Двухполюсники классифицируются следующим образом. 1. Пассивные двухполюсники – это такие, которые содержат только пассивные элементы и не содержат источников энергии. 2. Активные автономные двухполюсники содержат автономные источники. Если от двухполюсника отключить все внешние цепи и оставить его зажимы разомкнутыми, то обнаружится, что между ними есть напряжение (если замкнуть зажимы, то по ним потечет ток). 3. Активные неавтономные двухполюсники содержат пассивные элементы и только управляемые источники. Метод эквивалентного генератора применяют для расчета тока в одной ветви схемы не содержащей управляемого источника и, в общем случае, не имеющей индуктивных связей с оставшейся частью схемы. Он основан на теореме об эквивалентном генераторе: любую часть схемы, рассматриваемую относительно двух зажимов, можно заменить эквивалентным генератором с параметрами  , ,  , ,  при этом режим во внешней цепи не изменится. при этом режим во внешней цепи не изменится. МЭГ состоит в том, что сопротивление ветви, в которой требуется найти ток, считают сопротивлением нагрузки, а всю остальную часть схемы – активным двухполюсником. Этот двухполюсник заменяют эквивалентным генератором с параметрами  , ,  , ,  и находят ток через сопротивление нагрузки. и находят ток через сопротивление нагрузки.Примерный порядок расчета 1. Выбирают положительное направление тока IН в ветви с нагрузкой. 2.Удаляют сопротивление нагрузки  и в месте разрыва изображают стрелку, направленную так же, как ток и в месте разрыва изображают стрелку, направленную так же, как ток 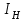 в ветви нагрузки. Стрелка указывает направление напряжения холостого хода в ветви нагрузки. Стрелка указывает направление напряжения холостого хода  . .3. Находят величину  : :- записывают уравнение по второму закону Кирхгофа для фиктивного контура, включающего  и не вносящего дополнительных неизвестных UJ; и не вносящего дополнительных неизвестных UJ;- в режиме холостого хода рациональным методом находят токи ветвей, входящие в уравнение для  ; ;- рассчитывают величину  . .4. Определяют входное сопротивление RBX относительно точек разрыва. Возможно несколько способов: а)  , ,где  - ток короткого замыкания, направленный также как - ток короткого замыкания, направленный также как 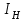 ; ;б) при отсутствии в схеме управляемых источников расчет входного сопротивления рациональнее всего выполнять сворачиванием схемы к входным зажимам пассивной схемы, полученной из активной схемы, путем замены автономных источников энергии их внутренними сопротивлениями; в) в схеме с автономными и управляемым источниками энергии автономные источники энергии заменяют их внутренними сопротивлениями. К зажимам полученной схемы подключают пробный источник и рассчитывают неизвестный пробный ток. Получают  как как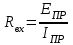 при одинаковом направлении 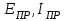 . .5. Рассчитывают ток через сопротивление нагрузки  . .Пример: Дано: 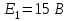 , ,  , , 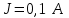 , , 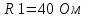 , ,  , ,  , , 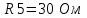 . .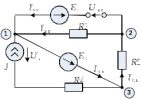 Рис. 2.6.1  => =>  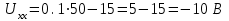 , , где  - ток - ток  в режиме холостого хода. в режиме холостого хода.  можно найти: можно найти:1) из системы уравнений по законам Кирхгофа  Откуда 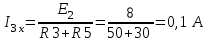 . .2) по методу наложения   , ,  , ,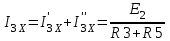  рис. 2.6.2 Согласно рис. 2.6.2: 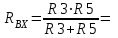  . .Тогда:  . .2.8 Передача мощности от активного двухполюсника в нагрузку Пусть есть активный двухполюсник и нагрузка, которая может меняться. Требуется выяснить, как зависит величина мощности нагрузки от  и, в частности, можно ли получить максимальную мощность нагрузки. Такая задача возникает при построении усилителей. и, в частности, можно ли получить максимальную мощность нагрузки. Такая задача возникает при построении усилителей.По теореме об эквивалентном генераторе активный двухполюсник заменим эквивалентным генератором.     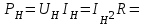 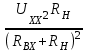 Дифференцируем  по по  иприравниваем производнуюк нулю иприравниваем производнуюк нулю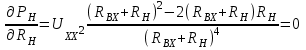 Тогда   Отсюда  . В линейных цепях без управляемых источников всегда . В линейных цепях без управляемых источников всегда 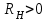 , значит , значит  . Такой режим работыдвухполюсника называют согласованным режимом. В этом режиме: . Такой режим работыдвухполюсника называют согласованным режимом. В этом режиме: , , , , . .Определить КПД передачи мощности в общем случае нельзя, так как нужно знать не только  , но и мощность, генерируемую внутри двухполюсника. Однако замену активного двухполюсника эквивалентным генератором проводим только из условия, что неизменным должен остаться только режим внешней цепи. , но и мощность, генерируемую внутри двухполюсника. Однако замену активного двухполюсника эквивалентным генератором проводим только из условия, что неизменным должен остаться только режим внешней цепи.  |
