|
|
Введение Основные определения Основные пояснения и термины
Трехфазная цепь является обычной цепью синусоидального тока с несколькими источниками.
Активная мощность трехфазной цепи равна сумме активных мощностей фаз
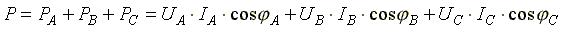 (7.5) (7.5)
Формула (7.5) используется для расчета активной мощности в трехфазной цепи при несимметричной нагрузке.
При симметричной нагрузке:
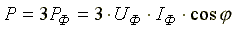
При соединении в треугольник симметричной нагрузки
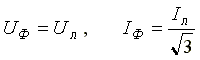
При соединении в звезду
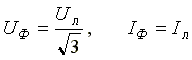 . .
В обоих случаях
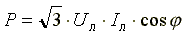 . .
8. Переходные процессы в линейных
электрических цепях 8.1. Общая характеристика переходных процессов
В электрических цепях возможны включения и отключения отдельных ветвей, короткие замыкания участков цепи, различного рода переключения. Любые изменения в электрических цепях можно представить в виде переключений или коммутаций. Характер коммутации указывается в схеме с помощью рубильника со стрелкой. По направлению стрелки можно судить, замыкается или размыкается рубильник.
При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому.
Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями. Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.
Первый закон. В любой ветви с индуктивностью ток не может изменяться скачком и в момент коммутации сохраняет то значение, которое он имел непосредственно перед моментом коммутации
iL (0+) = iL (0-),
где iL (0+) - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации;
iL (0-) - ток в индуктивности непосредственно перед коммутацией.
Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значение, которое оно имело непосредственно перед моментом коммутации.
uC (0+) = uC (0-),
где uC (0+) - напряжение на емкости в момент коммутации;
uC (0-) - напряжение на емкости непосредственно перед моментом коммутации.
Допущения, применяемые при анализе переходных процессов.
Полагают, что переходный процесс длится бесконечно большое время.
Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.
Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.
В соответствии с классическим методом расчета, переходный ток в ветви схемы представляют в виде суммы принужденного и свободного токов.
.
где iпр(t) - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону;
iсв(t) - свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости.
Свободный ток определяют по формуле:
.
Количество слагаемых в формуле равно числу реактивных элементов (индуктивностей и емкостей) в схеме.
P1, P2 - корни характеристического уравнения.
А1, А2 - постоянные интегрирования, определяются с помощью начальных условий.
Начальные условия - это переходные токи и напряжения в момент коммутации, в момент времени t, равный нулю.
Начальные условия могут быть независимыми или зависимыми.
Независимыми называют начальные условия, подчиняющиеся законам коммутации, законам постепенного, непрерывного изменения. Это напряжение на емкости uc(0) и ток в ветви с индуктивностью iL(0) в момент коммутации.
Остальные начальные условия: напряжение и ток в ветви с сопротивлением uR(0) и iR(0), напряжение на индуктивности uL(0) , ток в ветви с емкостью iC(0) - это зависимые начальные условия. Они не подчиняются законам коммутации и могут изменяться скачком.
8.2. Переходные процессы в цепях
с одним реактивным элементом
Короткое замыкание в R-L цепи
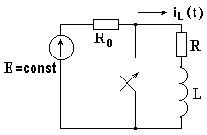
На рис. 8.1 изображена электрическая цепь, в которой включен источник постоянной ЭДС. В результате коммутации рубильник замыкается и образуется замкнутый на себя R-L контур.
До коммутации по индуктивности протекал ток
Этот ток создавал постоянное магнитное поле в индуктивной катушке.
Определим закон изменения тока в индуктивности после коммутации.
В соответствии с классическим методом
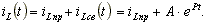
Принужденный ток после коммутации замыкается через рубильник, имеющий нулевое сопротивление, и через индуктивность не протекает. Индуктивный ток имеет только свободную составляющую
Магнитное поле, исчезая, индуктирует в индуктивной катушке ЭДС самоиндукции. Свободный ток в R-C контуре существует за счет этой электродвижущей силы.
Запишем уравнение для свободного тока в R-L контуре, используя второй закон Кирхгофа.
(8.1)
Ищем решение этого уравнения в виде экспоненты
.
Производная
.
Подставим значения свободного тока и производной тока в уравнение (8.1)
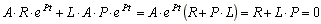 (8.2) (8.2)
Уравнение (8.2), полученное из уравнения (8.1), называется характеристическим.
- корень характеристического уравнения.
- постоянная времени переходного процесса, измеряется в секундах.
Постоянная времени τ - это интервал времени, за который переходный ток уменьшается в e раз.
.
Постоянную интегрирования А определяем с помощью начального условия.
В соответствии с первым законом коммутации,
.
Получим
Напряжение на индуктивности 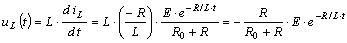 . .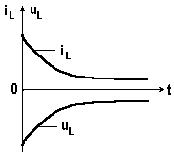
На рис. 8.2 изображены кривые переходного тока в ветви с индуктивностью и переходного напряжения на индуктивности. Переходный ток и напряжение по экспоненте стремятся к нулю. В инженерных расчетах полагают, что через интервал времени, равный (4 ÷ 5)τ, переходный процесс заканчивается.
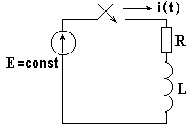
Подключение R-L цепи к источнику постоянной ЭДС
В схеме на рис. 8.3 до коммутации рубильник разомкнут. В результате коммутации рубильник замыкается и подключает R-L цепь к источнику постоянной ЭДС. Определим закон изменения тока i(t).
.
Принужденный ток в установившемся режиме после коммутации
.
В свободном режиме из схемы исключен внешний источник питания. Схема на рис. 8.3 без источника ЭДС ничем не отличается от схемы на рис. 8.1.
Свободный ток определяется по формуле
.
Запишем значение переходного тока для момента
коммутации, (t = 0). ,
откуда .
До коммутации рубильник был разомкнут, и ток в схеме отсутствовал.
Сразу после коммутации ток в индуктивности остается равным нулю.
.
.
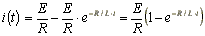 . .
Напряжение на индуктивности
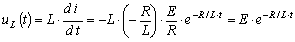 . .
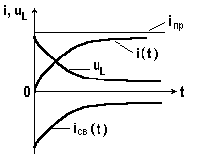
На рис. 8.4 изображены кривые переходного, принужденного, свободного токов и переходного напряжения на индуктивности.
Свободный ток и напряжение на индуктивности плавно уменьшаются до нуля. В момент коммутации свободный и принужденный токи одинаковы по абсолютной величине.
Переходный ток начинается при включении с нуля, затем возрастает, приближаясь к установившемуся постоянному значению.
9. Магнитные цепи 9.1. Основные определения
Как известно из курса физики, вокруг проводника с током появляется магнитное поле. Интенсивность магнитного поля характеризуется векторной величиной: напряженностью магнитного поля , измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором магнитной индукции , измеряемой в теслах (Тл). Напряженность магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей среды.
где μ0 - абсолютная магнитная проницаемость, Гн/м;
μ - относительное значение магнитной проницаемости, безразмерная величина;
μ0 = 4π·10-7 Гн/м.
В зависимости от величины относительной магнитной проницаемости, все вещества делятся на три группы.
К первой группе относятся диамагнетики: вещества, у которых μ< 1.
Ко второй группе относятся парамагнетики, вещества с μ >1.
К третьей группе относятся ферромагнетики, вещества с μ >> 1.
К ферромагнетикам принадлежат железо, никель, кобальт и многие сплавы из неферромагнитных веществ.
Магнитной цепью называется совокупность устройств, содержащих ферромагнитные вещества. Процессы в магнитных цепях описываются с помощью понятий магнитодвижущей силы, магнитного потока.
Магнитным потоком называется поток вектора магнитной индукции через поверхность S
.
Магнитный поток измеряется в веберах (Вб).
Источником магнитодвижущей силы является либо постоянный магнит, либо электромагнит (катушка, обтекаемая током).
Магнитодвижущая сила электромагнита
где I - ток, протекающий в катушке;
W - число витков катушки.
В магнитных цепях используется свойство ферромагнитного материала тысячекратно усиливать магнитное поле катушки с током за счет собственной намагниченности.
9.2. Свойства ферромагнитных материалов
Поместим ферромагнитный материал внутри катушки с током. Сначала, с увеличением напряженности намагничивающего поля, магнитная индукция быстро возрастает. Затем, из-за насыщения материала, при дальнейшем увеличении напряженности магнитного поля магнитная индукция почти не меняется. При уменьшении напряженности намагничивающего поля кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса. Явление гистерезиса заключается в том, что изменение магнитной индукции запаздывает от изменения намагничивающего поля. Кривая зависимости B(H), получающаяся при циклическом перемагничивании ферромагнитного материала, называется петлей гистерезиса. Эта кривая изображена на рис. 9.1. Чем больше площадь петли, тем больше потери на перемагничивание, нагревающие материал.
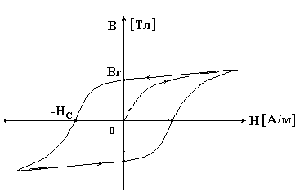
Рис. 9.1
Значение магнитной индукции при напряженности намагничивающего поля, равном нулю, называется остаточной магнитной индукцией Br, или остаточной намагниченностью.
Напряженность магнитного поля НС при В = 0 называется коэрцитивной силой.
Ферромагнитные материалы с большим значением коэрцитивной силы () называются магнитотвердыми. Из этих материалов изготавливают постоянные магниты.
Ферромагнитные материалы с малым значением коэрцитивной силы () называются магнитомягкими. Эти материалы используют в магнитопроводах электрических машин и трансформаторов.
Таким образом, зависимости B = f(H) у ферромагнитных материалов нелинейные.
Эти зависимости приводятся в справочниках в табличной форме или в виде кривых, называемых кривыми намагничивания.
9.3. Расчет магнитных цепей
Основным законом, используемым при расчетах магнитных цепей, является закон полного тока.
(9.1)
Он формулируется следующим образом: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром. Если контур интегрирования охватывает катушку с числом витков W, через которую протекает ток I, то алгебраическая сумма токов , где F - магнитодвижущая сила.
Обычно контур интегрирования выбирают таким образом, чтобы он совпадал с силовой линией магнитного поля, тогда векторное произведение в формуле (9.1) можно заменить произведением скалярных величин H·dl. В практических расчетах интеграл заменяют суммой и выбирают отдельные участки магнитной цепи таким образом, чтобы H1, H2, . . . вдоль этих участков можно было считать приблизительно постоянными. При этом (9.1) переходит в
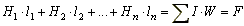 (9.2) (9.2)
где l1, l2, …, ln - длины участков магнитной цепи;
H1·l1, H2·l2 - магнитные напряжения участков цепи. Магнитным сопротивлением участка магнитной цепи называется отношение магнитного напряжения рассматриваемого участка к магнитному потоку в этом участке
,
где S - площадь поперечного сечения участка магнитной цепи,
l - длина участка.
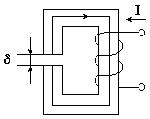
Рассмотрим расчет магнитной цепи, изображенной на рис. 9.2.
Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S.
lср - длина средней силовой линии магнитного поля в магнитопроводе;
δ - толщина воздушного зазора.
На магнитопроводе размещена обмотка, по которой протекает ток I.
Рис. 9.2
Прямая задача расчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу F. Определим магнитную индукцию в магнитопроводе
.
По кривой намагничивания найдем значение напряженности магнитного поля H, соответствующее величине В.
Напряженность магнитного поля в воздушном зазоре
.
Магнитодвижущая сила обмотки
.
При обратной задаче расчета магнитной цепи по заданному значению магнитодвижущей силы требуется определить магнитный поток. Расчет такой задачи выполняется с помощью магнитной характеристики цепи F = f(Ф).
Для построения такой характеристики необходимо задаться несколькими значениями Ф и найти соответствующие значения F. С помощью магнитной характеристики по заданной магнитодвижущей силе определяется магнитный поток.
|
|
|
 Скачать 5.72 Mb.
Скачать 5.72 Mb.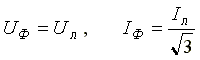
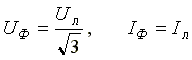 .
.





