Введение Основные определения Основные пояснения и термины

• Название: Введение Основные определения Основные пояснения и термины
• Анкор: Elektrotekhnika_3.rtf
• Дата: 20.07.2018
• Размер: 5.72 Mb.
• Имя файла: Elektrotekhnika_3.rtf
• Тип: Анализ; #21747
• страница: 12 из 13

7.3. Соединение в треугольник. Схема, определения

       Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке.
        На рис. 7.3 изображена трехфазная цепь, соединенная треугольником. Как видно
из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы.

U_л = U_ф

       I_A, I_B, I_C - линейные токи;

       I_ab, I_bc, I_ca- фазные токи.

       Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с.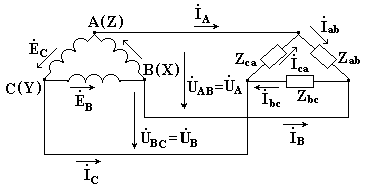





Рис. 7.3

       Линейный ток равен геометрической разности соответствующих фазных токов.
    На рис. 7.4  изображена  векторная  диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.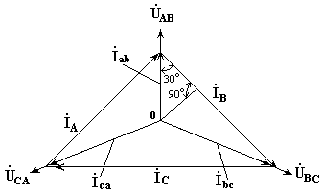



Рис. 7.4

       Из векторной диаграммы видно, что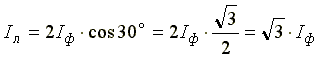

,

I_л = √3 I_ф при симметричной нагрузке.

     Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме "звезда". Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.

7.4. Расчет трехфазной цепи, соединенной звездой

       Трехфазную цепь,   соединенную звездой, удобнее всего рассчитать методом двух узлов.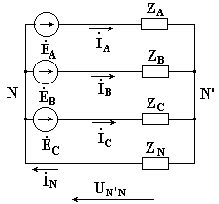




       На рис. 7.5 изображена трехфазная цепь при соединении звездой. В общем случае сопротивления фаз нагрузки неодинаковы (Z_A ≠ Z_B ≠ Z_C )

       Нейтральный провод имеет конечное сопротивление Z_N .
       В схеме между нейтральными точками источника и нагрузки возникает узловое напряжение или напряжение смещения нейтрали.
       Это напряжение определяется по формуле (7.2).

                Рис.7.5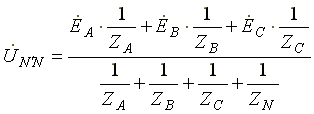

     (7.2)

       Фазные токи определяются по формулам (в соответствии с законом Ома для активной ветви):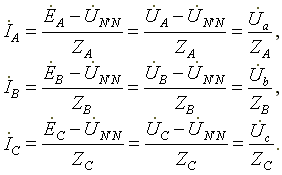

     (7.3)

       Ток в нейтральном проводе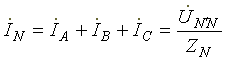

                 (7.4)

       Частные случаи.

    1. Симметричная нагрузка.   Сопротивления фаз нагрузки   одинаковы и равны некоторому активному сопротивлению Z_A = Z_B = Z_C = R.
       Узловое напряжение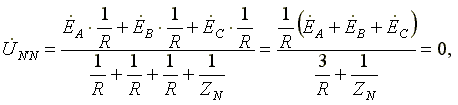

,

потому что трехфазная система ЭДС симметрична,     .

        Напряжения фаз нагрузки и генератора одинаковы:

     Фазные токи  одинаковы по  величине и совпадают по фазе со своими фазными напряжениями. Ток в нейтральном проводе отсутствует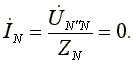



       В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.

      На рис. 7.6 изображена векторная диаграмма трехфазной цепи для симметричной нагрузки.

       2. Нагрузка несимметричная,   R_A< R_B = R_C, но сопротивление нейтрального провода равно нулю:  Z_N = 0. Напряжение смещения нейтрали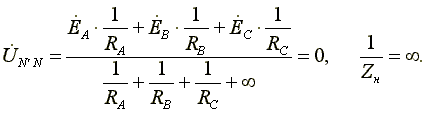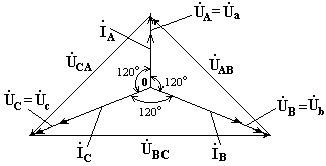





рис. 7.6

       Фазные напряжения нагрузки и генератора одинаковы

       Фазные токи определяются по формулам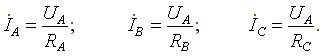



      Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.

       На  рис.  7.7  приведена  векторная  диаграмма    трехфазной    цепи,    соединенной    звездой,    с нейтральным    проводом,    имеющим     нулевое     сопротивление,    нагрузкой   которой      являются   неодинаковые   по    величине    активные  сопротивления.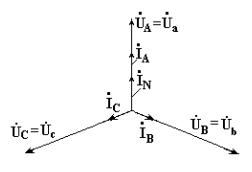




                    Рис. 7.7

       3. Нагрузка несимметричная, R_A< R_B = R_C, нейтральный провод отсутствует,


       В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле: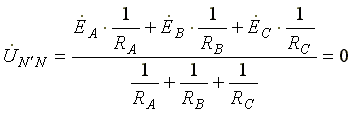



      Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора.
    Из-за напряжения  смещения нейтрали фазные  напряжения нагрузки становятся неодинаковыми.
      Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.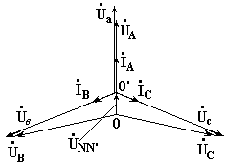

       На рис. 7.8 изображена векторная диаграмма трехфазной цепи с несимметричной нагрузкой и оборванным нейтральным проводом. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки, т.е. с включением данного нейтрального провода фазные напряжения нагрузки становятся одинаковыми.
                Рис. 7.8