Введение Основные определения Основные пояснения и термины

• Название: Введение Основные определения Основные пояснения и термины
• Анкор: Elektrotekhnika_3.rtf
• Дата: 20.07.2018
• Размер: 5.72 Mb.
• Имя файла: Elektrotekhnika_3.rtf
• Тип: Анализ; #21747
• страница: 10 из 13

6.5. Индуктивная катушка в цепи синусоидального тока

     Сначала рассмотрим идеальную индуктивную катушку, активное сопротивление которой равно нулю. Пусть по идеальной катушке с индуктивностью L протекает синусоидальный ток . Этот ток создает в индуктивной катушке переменное магнитное поле, изменение которого вызывает в катушке ЭДС самоиндукции

     (6.9)

     Эта ЭДС уравновешивается напряжением, подключенным к катушке: u = e_L = 0.

     (6.10)

     Таким образом, ток в индуктивности отстает по фазе от напряжения на 90^o из-за явления самоиндукции.
     Уравнение вида (6.10) для реальной катушки, имеющей активное сопротивление R, имеет следующий вид:

     (6.11)

     Анализ выражения (6.11) показывает, что ЭДС самоиндукции оказывает препятствие (сопротивление) протеканию переменного тока, из-за чего ток в реальной индуктивной катушке отстает по фазе от напряжения на некоторый угол φ (0^o< φ < 90^o), величина которого зависит от соотношения R и L.      Выражение (6.11) в комплексной форме записи имеет вид: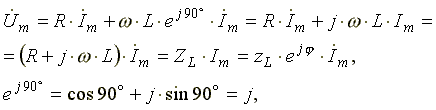

     (6.12)

      где Z_L - полное комплексное сопротивление индуктивной катушки ;
            Z_L - модуль комплексного сопротивления;
            - начальная фаза комплексного сопротивления;
          - индуктивное сопротивление (фиктивная величина, характеризующая реакцию электрической цепи на переменное магнитное поле).
      Полное сопротивление индуктивной катушки или модуль комплексного сопротивления

.

       Комплексному уравнению (6.12) соответствует векторная диаграмма (рис.6.5).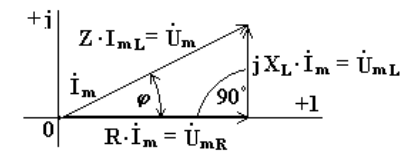


Рис. 6.5

       Из анализа диаграммы видно, что вектор напряжения на индуктивности опережает вектор тока на 90^o.
    В цепи  переменного тока напряжения на  участках цепи складываются не арифметически, а геометрически.
       Если мы поделим стороны треугольника напряжений на величину тока I_m, то перейдем к подобному треугольнику сопротивлений (рис. 6.6).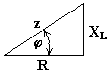

   

Рис. 6.6

 Из треугольника сопротивлений получим несколько формул:
                     ;                     ;
    

;

;           .

6.6. Емкость в цепи синусоидального тока

     Если к конденсатору емкостью C подключить синусоидальное напряжение, то в цепи протекает синусоидальный ток

;

.    (6.13)

      Из анализа выражений 6.13 следует, что ток опережает напряжение по фазе на 90^o.

      Выражение (6.13) в комплексной форме записи имеет вид: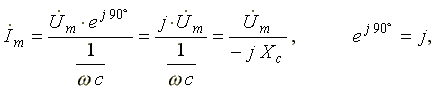

,    (6.14)

       где - емкостное сопротивление, фиктивная расчетная величина, имеющая размерность сопротивления.

        Если комплексное сопротивление индуктивности положительно
       , то комплексное сопротивление емкости отрицательно

        .

       На рис. 6.7 изображена векторная диаграмма цепи с емкостью.
       Вектор тока опережает вектор напряжения на 90^o.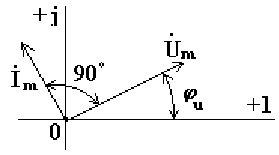


Рис. 6.7

6.10. Мощность в цепи синусоидального тока

     Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток.
     Пусть мгновенные напряжение и ток определяются по формулам:

     

     Тогда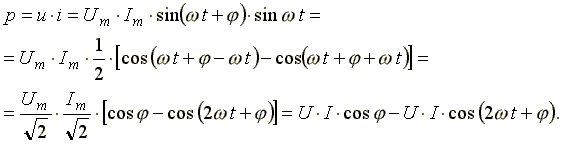

          (6.23)

     Среднее значение мгновенной мощности за период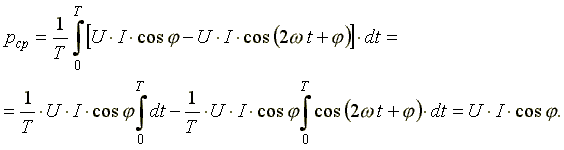



     Из треугольника сопротивлений ,      а      .

     Получим еще одну формулу:

.

     Среднее арифметическое значение мощности за период называют активной мощностью и обозначают буквой P.
   Эта мощность измеряется в ваттах и характеризует необратимое преобразование электрической энергии в другой вид энергии, например, в тепловую, световую и механическую энергию.
     Возьмем реактивный элемент (индуктивность или емкость). Активная мощность в этом элементе , так как напряжение и ток в индуктивности или емкости различаются по фазе на 90^o. В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов.
   Происходит обратимый  процесс в  виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.
     Преобразуем выражение (6.23):



     где - мгновенная мощность в активном сопротивлении;

      - мгновенная мощность в реактивном элементе (в индуктивности или в емкости).
   Максимальное или амплитудное значение мощности p₂ называется реактивной мощностью

      ,

     где x - реактивное сопротивление (индуктивное или емкостное).
     Реактивная мощность, измеряемая в вольтамперах реактивных, расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.
     Амплитудное значение суммарной мощности p = p₁ + p₂ называется полной мощностью.
   Полная  мощность,  измеряемая в вольтамперах, равна произведению действующих значений напряжения и тока:

      ,

     где z - полное сопротивление цепи.
   Полная мощность характеризует предельные возможности источника энергии. В электрической цепи можно использовать часть полной мощности

,

       где 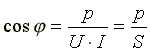   - коэффициент мощности или "косинус "фи".

  Коэффициент  мощности  является одной из важнейших характеристик электротехнических устройств. Принимают специальные меры к увеличению коэффициента мощности.
      Возьмем треугольник сопротивлений и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 6.18).

     Из треугольника мощностей получим ряд формул: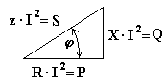

,      ,

             Рис.6.18
                                                                ,      .
     При анализе электрических цепей символическим методом используют выражение комплексной мощности, равное произведению комплексного напряжения на сопряженный комплекс тока.
     Для цепи, имеющей индуктивный характер (R-L цепи)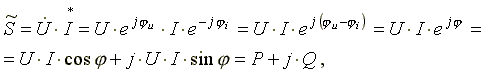

,

       где   
      - комплекс напряжения;
      - комплекс тока;
      - сопряженный комплекс тока;
      - сдвиг по фазе между напряжением и током.
     , ток как в R-L цепи, напряжение опережает по фазе ток.

     Вещественной частью полной комплексной мощности является активная мощность.
     Мнимой частью комплексной мощности - реактивная мощность.
     Для цепи, имеющей емкостной характер (R-С цепи), . Ток опережает по фазе напряжение.

.

     Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, - положительна, а в цепи с емкостным характером - отрицательна.