лекции по ОТИ. Введение. Понятие информации. Информация и данные

• Название: Введение. Понятие информации. Информация и данные
• Анкор: лекции по ОТИ
• Дата: 29.08.2022
• Размер: 376.35 Kb.
• Имя файла: лекции по ОТИ.docx
• Тип: Лекции; #655458
• страница: 4 из 7

Линия связи

Кодирующее устройство

Декодирую-щее устройство

Решающее устройство


Передатчик

Получатель

Канал связи

Система состоит из отправителя информации, линии связи и получателя информации. Сообщение для передачи его в соответствующий адрес должно быть предварительно преобразовано в сигнал. Под сигналом понимается изменяющаяся физическая величина, отображающее сообщение. Сигнал – материальный переносчик сообщения, т.е. изменяющаяся физическая величина, обеспечивающая передачу информации по линии связи. Физическая среда, по которой происходит передача сигналов от передатчика к приемнику, называется линией связи.

В современной технике нашли применение электрические, электромагнитные, световые, механические, звуковые, ультразвуковые сигналы. Для передачи сообщений необходимо принять тот переносчик, который способен эффективно распределяться по используемой в системе линии связи (FE: по радиолинии эффективно распределяется только электромагнитные колебания высоких частот – от сотен кГц до дес. тысяч МГц).

2. 
   Классификация сигналов по дискретно-непрерывному признаку.
   

Все сообщения по характеру изменяющиеся во времени можно разделить на непрерывные и дискретные. Непрерывные по времени сообщения отображаются непрерывной функцией времени. Дискретные по времени сообщения характеризуются тем, что поступают в определенные моменты времени и описываются дискретной функцией t.

Сообщения также можно разделить на непрерывные и дискретные по множеству. Непрерывные множеству сообщения характеризуются тем, что функция, их описывающая, может принимать непрерывное множество значений. Дискретные по множеству сообщения – это сообщения, которые могут быть описаны с помощью конечного набора чисел или дискретных значений некоторой функции.

Дискретности по множеству и времени не связаны друг с другом. Рассмотрим возможные типы сообщений подробнее.

Пусть сигнал описывается функцией X (t)

1) непрерывные по множеству и времени, или просто непрерывные; (рис. 1.2)

2) непрерывные по множеству и дискретные по времени; (рис. 1.3)

3) дискретные по множеству и непрерывные по времени; (рис. 1.4)

4) дискретные по множеству и времени, или просто дискретные;

(рис. 1.5)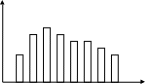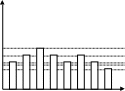








В процессе преобразования дискретных сообщений в сигнал происходит кодирование сообщения. В широком смысле кодированием называется преобразование сообщений в сигнал. В узком смысле кодирование – это отображение дискретных сообщений сигналами в виде определенных сочетаний символов. Устройство, осуществляющее кодирование называется кодером.

При передаче сигналы подвергаются воздействию помех. Под помехами подразумеваются любые мешающие внешние возмущения или воздействия (атмосферные помехи, влияние посторонних источников сигналов), а также искажения сигналов в самой аппаратуре (аппаратурные помехи), вызывающие случайное отклонение принятого сообщения (сигнала) от передаваемого.

На приемной стороне осуществляется обратная операция декодирования, т.е. восстановление по принятому сигналу переданного сообщения.

Решающее устройство, помещенное после приемника, осуществляет обработку принятого сигнала с целью наиболее полного извлечения из него информации.

Декодирующее устройство, (декодер)преобразует принятый сигнал к виду удобному для восприятия получателем.

Совокупность средств, предназначенных для передачи сигнала, называется каналом связи.

3. 
   Квантование и кодирование сигналов
   

Физические сигналы являются непрерывными функциями времени. Чтобы преобразовать непрерывный, в частности, аналоговый сигнал в цифровую форму используются аналого-цифровые преобразователи (АЦП). Процедуру аналого-цифрового преобразования сигнала обычно представляют в виде последовательности трех операций: дискретизации, квантования и кодирования.

Операция дискретизации заключается в определении выборки моментов времени измерения сигнала. Операция квантования состоит в считывании значений координаты сигнала в выбранные моменты измерения с заданным уровнем точности, а операция кодирования - в преобразовании полученных измерений сигнала в соответствующие значения некоторого цифрового кода или кодовой комбинации, которые затем передаются по каналам связи.

Процедуру восстановления непрерывного сигнала из цифрового представления также можно представить в виде двух операций: декодирования и демодуляции. Операция декодирования выполняет операцию обратную операции кодирования, т.е. преобразует последовательность заданных значений кодовой комбинации (кодовых слов) в последовательность измерений, следующих друг за другом через заданные интервалы времени дискретизации. Операция демодуляции выполняет интерполяцию или восстановление непрерывного сигнала по его измерениям. Преобразование сигнала из цифровой формы в непрерывный сигнал осуществляется цифро-аналоговыми преобразователями (ЦАП). Считается, что система аналого-цифрового и цифро-аналогового преобразований адекватна сигналу, если восстановленный непрерывный сигнал (копия) соответствует исходному непрерывному сигналу (оригиналу) с заданной погрешностью.

3. 
   Квантование по уровню
   

При квантовании по уровню непрерывное множество значений функции x(t) заменяется множеством дискретных значений. Для этого в диапазоне непрерывных значений функции x(t) выбирается конечное число дискретных значений этой функции (дискретных уровней) и в процессе квантования значение функции x(t) в каждый момент времени заменяется ближайшим дискретным значением. В результате квантования образуется ступенчатая функция x_g(t).

Квантование по уровню практически может осуществляться двумя способами. При первом способе квантования мгновенное значение функции x(t) заменяется меньшим дискретным значением. При втором способе квантования мгновенное значение функции x(t) заменяется ближайшим меньшим или большим дискретным значением в зависимости от того, какое из этих значений ближе к мгновенному значению функции. В этом случае переход ступенчатой функции с одной ступени на другую происходит в те моменты, когда первоначальная непрерывная функция x(t) пересекает середину между соответствующими соседними дискретными уровнями.

Расстояние между дискретными соседними уровнями называется интервалом или шагом квантования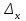

Различают равномерное квантование по уровню, при котором шаг квантования постоянен, и неравномерное квантование по уровню, когда шаг квантования непостоянен. На практике преимущественное применение получило равномерное квантование в связи с простотой его технической реализации.

3. 
   Квантование по времени
   

Рассмотрим сущность понятия дискретизации сигнала x(t) применительно к детерминированной функции.

Дискретизация сигнала x(t) связана с заменой промежутка изменения независимой переменной некоторым множеством точек, т.е. операции дискретизации соответствует отображение

x(t) x(t_i)

x(t) – функция, описывающая сигнал

x(t_i) – функция, описывающая сигнал, полученный в результате дискретизации,

то есть в результате дискретизации исходная функция x(t) заменяется совокупностью отдельных значений x(t_i). По значениям x(t_i) можно восстановить исходную функцию x(t) с некоторой погрешностью. Функция, полученная в результате восстановления (интерполяции) по значениям x(t_i) , называется воспроизводящей и обозначается через V(t).

При обработке сигналов дискретизация по t должна производится таким образом, чтобы по отсчетным значениям x(t_i) можно было получить воспроизводящую функцию V(t), которая с заданной точностью отображает исходную функцию x(t).

При дискретизации сигналов приходится решать вопрос о том, каков должен быть шаг дискретизации: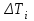

=t_i-t_i-1

Контрольные вопросы:

1. 
   Что понимают под линией связи?
   
2. 
   Какое устройство называется декодером?
   
3. 
   Какое устройство называется решающим?
   
4. 
   Какое устройство называются декодирующим?
   
5. 
   Что называют шагом квантования?
   
6. 
   Дайте определение квантования по уровню.
   
7. 
   Дайте определение квантования по времени.
   

Тема: Пропускная способность канала связи. Теорема Шеннона

Определим пропускную способность канала как максимальное количество информации, которое можно передавать по нему в единицу времени:

C = max{Ixy}/ tx (бит/с) (1)

Для канала без помех справедливо условие I_xy = H_x, а потому его пропускная способность:

C_бп = max{Hx}/ tx = log₂m / tx (2)

В частном случае передачи двоичных разрядов (m = 2) справедливо

С_бп = 1/tx (3).

Для нас важно, как соотносится величина С_бп с потоком информации источника H`z, который определяется по формуле

H`z = Hz/tz (бит/с) (4).

Пропускная способность канала используется полностью, когда H`z = C. Между тем, уменьшение энтропии Hz может привести к сокращению информационного потока. Чтобы его увеличить, требуется сократить время tz. Если учесть, что

tz = tx * lср, где lср - средняя длина кода символа, то становится ясно: чтобы полнее использовать пропускную способность канала для любого источника, нужно рационально кодировать сообщения, по возможности сокращая величину lср.

Если записать условие полного использования пропускной способности канала H`z = C в развернутом виде, то для канала без помех оно будет иметь вид:

Hz/tz = log₂m/tx (5),

а с учетом tz = tx * lср и log₂m = 1 (при m=2) мы получим условие:

lср = Hz (6)

По сути, доказательство этой так называемой теоремы Шеннона о кодировании для канала без помех сводится к нахождению процедуры, позволяющей получить требуемый код. Эта процедура, именуемая эффективным кодированием, была предложена самим Шенноном и в дальнейшем усовершенствована (с точки зрения удобства ее практического применения) Хаффменом.

В обоих случаях речь идет о посимвольном кодировании и величина Hz имеет значение безусловной энтропии. В принципе можно пойти дальше и рассматривать кодирование цепочек символов. В этом случае Hz будет иметь смысл условной энтропии порядка l, где l - максимальная длина цепочки. О "цепочечном" кодировании речь впереди, а пока мы рассмотрим классический подход к эффективному кодированию на уровне символов.

Пропускная способность дискретного канала с помехами

Рассмотрим теперь вариант, когда помехи в канале вызывают появление ошибок с вероятностью p₀. В этом случае из соотношения 3.1 следует:

C = max {Hx - Hx/y}/ tx = (log₂m - Hx/y) / tx (7)

Рассмотрим наиболее распространенный случай так называемого двоичного симметричного канала. При этом m = 2 (log₂m = 1), а вероятности ошибки “переход "1" в "0” ” “переход "0" в "1" ” одинаковы.

Если теперь рассмотреть в качестве случайного события передачу разряда кода с ошибкой (вероятность p₀), то, используя формулу (9) для определения энтропии, получим:

Hx/y = Hy/x = -p₀ log₂p₀ - (1 - p₀) log₂(1 - p₀) (8)

С учетом этого (9) преобразуется к виду:

C = [1 - p₀log₂p₀ - (1 - p₀)log₂(1 - p₀)]/tx (9)

Таким образом, пропускная способность симметричного двоичного канала с помехами определяется только скоростью передачи разрядов кода (Vx = 1/tx) и вероятностью ошибок.

Клод Шеннон показал, что за счет кодирования пропускную способность канала с помехами также можно использовать максимально полно (напомним, что сама она будет ниже, чем у канала без помех).

Способ кодирования, который позволяет этого добиться, основан на использовании избыточных кодов, когда каждый информационный блок защищается контрольными разрядами и чем больше длина блока, тем меньше удельный вес этих избыточных разрядов, позволяющих обнаружить и исправить ошибки.

4. Пропускная способность непрерывного канала с помехами

На рис. 1 была показана модель дискретного канала передачи данных. Напомним, что с помощью дискретизации и квантования к дискретному виду можно свести любое непрерывное сообщение. Однако, если шаг квантования dx и шаг дискретизации dt устремить к нулю, то из модели рис. 1 мы получим частный случай непрерывного канала.



Рис. 1

Источник И передает в канал непрерывное сообщение Z(t).

Формирователь сигналов Фс преобразует его в сигнал X (t), приспособленный для передачи по аналоговому каналу.

В линии связи ЛС на сигнал воздействуют случайные аддитивные помехи e(t) (для помех такого типа справедливо соотношение Y(t) = X(t) + e(t)).

Устройство распознавания сигнала восстанавливает сообщение Z(t) по полученному Y(t).

В этой схеме стадия кодирования вообще не рассматривается. Однако подход (кстати, предложенный опять-таки Клодом Шенноном) основан на тех же принципах, что и для дискретного канала, потому нам целесообразно рассмотреть этот вопрос именно здесь.

Вернемся к определению пропускной способности канала связи:

Cбп = max{Ixy} / tx = max{Hx } / tx (10)

Величина tx в нашем случае соответствует шагу дискретизации сигнала dt. Согласно теореме Котельникова, непрерывный сигнал можно полностью восстановить по его дискретным отсчетам, если шаг дискретизации dt вдвое меньше периода самой высокочастотной составляющей f_m сигнала (dt = 1/2f_m). Учитывая, что любой физический канал связи всегда имеет ограниченную полосу частот, которые он в состоянии пропустить, величину f_m (а следовательно и dt) можно определить исходя из характеристик канала.

Если значение dx конечно, то непрерывный канал можно рассматривать как дискретный с объемом алфавита m = x_m/dx + 1. Если к тому же в канале отсутствуют помехи (Hx/y = 0), то соотношение (4.11) можно преобразовать к виду:

C = max {Hx} / dt = 2f_m * log₂m = 2f_m * log₂ (x_m/ dx + 1) (11)

Отсюда видно, что пропускная способность непрерывного канала без помех (dx -> 0) стремится к бесконечности. Однако, в реальном канале помехи присутствуют всегда, при этом сколько бит информации удается "нагрузить" на один дискретный отсчет, зависит от соотношения мощности полезного сигнала на входе приемника и помехи Pс/Pп.

Клод Шеннон показал, что в случае наиболее "неприятной" помехи типа "белый шум", чья мощность равномерно распределена во всей полосе частот канала, справедливо соотношение:

Cn = fm log₂(Pс/Pп + 1) (12)

Доказательство этой теоремы Шеннона о пропускной способности непрерывного канала весьма громоздко и мы не станем его рассматривать. Остановимся на анализе самой формулы. Итак пропускная способность непрерывного канала с помехами:

- пропорциональна ширине полосы частот канала fm;

- возрастает с увеличением отношения полезный сигнал/помеха (в этом случае будет уверенно распознаваться на фоне помех);

- не равна нулю даже при Pc << Pп (то-есть, передачу информации принципиально можно вести сигналами более слабыми, чем помехи).

Мы вернемся к использованию соотношения Шеннона 4.13 при рассмотрении вопросов передачи сигналов.

Контрольные вопросы:

1. 
   Определите пропускную способность непрерывного канала без помех.
   
2. 
   Определите пропускную способность непрерывного канала с помехами.
   
3. 
   Опишите назначение: источника, формирователя сигналов.
   
4. 
   Как воздействует сигнал в линии связи?
   
5. 
   Как работает устройство распознавания?