лекции по ОТИ. Введение. Понятие информации. Информация и данные
 Скачать 376.35 Kb. Скачать 376.35 Kb.
|
|
Тема: Методы повышения помехозащищенности и помехоустойчивости передачи и приема данных. Одна и та же линия связи может использоваться для передачи сигналов между многими источниками и приемниками, т.е. линия связи может обслуживать несколько каналов. При синтезе систем передачи информации приходится решать две основные проблемы, связанные с передачей сообщений: обеспечение помехоустойчивости передачи сообщений обеспечение высокой эффективности передачи сообщений Под помехоустойчивостью понимается способность информации противостоять вредному воздействию помех. При данных условиях, т.е. при заданной помехе, помехоустойчивость определяет верность передачи информации. Под верностью понимается мера соответствия принятого сообщения (сигнала) переданному сообщению (сигналу). Под эффективностью системы передачи информации понимается способность системы обеспечивать передачу заданного количества информации наиболее экономичным способом. Эффективность характеризует способность системы обеспечить передачу данного количества информации с наименьшими затратами мощности сигнала, времени и полосы частот. Теория информации устанавливает критерии оценки помехоустойчивости и эффективности информационных систем, а также указывает общие пути повышения помехоустойчивости и эффективности. Повышение помехоустойчивости практически всегда сопровождается ухудшением эффективности и наоборот. Методы повышения помехоустойчивости В основах всех способов повышения помехоустойчивости информационных систем лежит использование определенных различий между полезным сигналом и помехой. Поэтому для борьбы с помехами необходимы априорные сведения о свойствах помехи и сигнала. В настоящее время известно большое число способов повышения помехоустойчивости систем. Эти способы удобно разбить на две группы. I группа – основана на выборе метода передачи сообщений. II группа – связана с построением помехоустойчивых приемников. Простым и применяемым способом повышения помехоустойчивости является увеличение отношения сигнал/помеха за счет увеличения мощности передатчика. Но этот метод может оказаться экономически не выгодным, так как связан с существенным ростом сложности и стоимости оборудования. Кроме того, увеличение мощности передачи сопровождается усилением мешающего действия данного канала на другие. Важным способом повышения помехоустойчивости передачи непрерывных сигналов является рациональный выбор вида модуляции сигналов. Применяя виды модуляции, обеспечивающие значительное расширение полосы частот сигнала, можно добиться существенного повышения помехоустойчивости передачи. Радикальным способом повышения помехоустойчивости передачи дискретных сигналов является использование специальных помехоустойчивых кодов. При этом имеется два пути повышения помехоустойчивости кодов: Выбор таких способов передачи, которые обеспечивают меньшую вероятность искажения кода; Увеличение корректирующих свойств кодовых комбинаций. Этот путь связан с использованием кодов, позволяющих обнаруживать и устранять искажения в кодовых комбинациях. Такой способ кодирования связан с введением в код дополнительных, избыточных символов, что сопровождается увеличением времени передачи или частоты передачи символов кода. Повышение помехоустойчивости передачи может быть также достигнуто путем повторной передачи одного и того же сообщения. На приемной стороне сравниваются полученные сообщения и в качестве истинных принимаются те, которые имеют наибольшее число совпадений. Чтобы исключить неопределенность при обработке принятой информации и обеспечить отбор по критерию большинства, сообщение должно повторяться не менее трёх раз. Этот способ повышения помехоустойчивости связан с увеличением времени передачи. Системы с повторением передачи дискретной информации делятся на системы с групповым суммированием, у которых сравнение производится по кодовым комбинациям, и на системы с посимвольным суммированием, у которых сравнение осуществляется по символам кодовых комбинаций. Посимвольная проверка является более эффективной, чем групповая. Разновидность систем, у которых повышение помехоустойчивости достигается за счет увеличения времени передачи, являются системы с обратной связью. При наличии искажений в передаваемых сообщениях информация, поступающая по обратному каналу, обеспечивает повторение передачи. Наличие обратного канала приводит к усложнению системы. Однако в отличие от систем с повторением передачи в системах с обратной связью повторение передачи будет иметь место лишь в случае обнаружения искажений в передаваемом сигнале, т.е. избыточность в целом оказывается меньшей. Помехоустойчивый прием состоит в использовании избыточности, а также априорных сведений о сигналах и помехах для решения оптимальным способом задачи приема: обнаружения сигнала, различия сигналов или восстановления сообщений. В настоящее время для синтеза оптимальных приемников широко используется аппарат теории статистических решений. Ошибки приемника уменьшаются с увеличением отношения сигнал/помеха на входе приемника. В связи с этим часто производят предварительную обработку принятого сигнала с целью увеличения отношений полезной составляющей к помехе. К таким методам предварительной обработки сигналов относится метод ШОУ (сочетание широкополосного усилителя, ограничителя и узкополосного усилителя), селекция сигналов по длительности, метод компенсации помехи, метод фильтрации, корреляционный метод, метод накопления и др. Рассмотрим простые практические способы построения кодов, способных обнаруживать и исправлять ошибки. Ограничимся рассмотрением двоичных каналов и равномерных кодов. Метод контроля четности. Это простой способ обнаружения некоторых из возможных ошибок. Будем использовать в качестве разрешенных половину возможных кодовых комбинаций, а именно те из них, которые имеют четное число единиц (или нулей). Однократная ошибка при передаче через канал неизбежно приведет к нарушению четности, что и будет обнаружено на выходе канала. Очевидно, что трехкратные, пятикратные и вообще ошибки нечетной кратности ведут к нарушению четности и обнаруживаются этим методом, в то время как двукратные, четырехкратные и вообще ошибки четной кратности – нет. Практическая техника кодирования методом контроля четности следующая. Из последовательности символов, подлежащих передаче через канал, выбирается очередной блок из k-1символов, называемых информационными, и к нему добавляется k-й символ, называемый контрольным. Значение контрольного символа выбирается так, чтобы обеспечить четность получаемого кодового слова, т.е. чтобы сделать его разрешенным. Метод контроля четности представляет значительную ценность и широко применяется в тех случаях, в которых вероятность появления более одной ошибки пренебрежимо мала (во многих случаях, если наверняка знать, что кодовое слово принято с ошибкой, имеется возможность запросить повторную передачу). В то же время избыточность кода увеличивается минимально и незначительно при больших k(в k/( k-1)раз). Метод контрольных сумм. Рассмотренный выше метод контроля четности может быть применен многократно для различных комбинаций разрядов передаваемых кодовых слов – и это позволит не только обнаруживать, но и исправлять определенные ошибки. Контрольные вопросы: Дайте определение помехоустойчивости. Что понимают под эффективностью системы? Перечислите методы повышения помехоустйчивости. Расскажите о методе контроля четности. Что собой представляет метод контрольных сумм? Тема: Понятие об оптимальном кодировании информации Большинство кодов, используемых при кодировании информации без учета статистических свойств источника и помех в канале связи, основано на системах счисления (двоичной, десятичной, восьмеричной, шестнадцатеричной). Общепризнанным в настоящее время является позиционный принцип образования системы счисления. Значение каждого символа (цифры) зависит от его положения - позиции в ряду символов, представляющих число. Единица каждого следующего разряда больше единицы предыдущего в т раз, где т - основание системы счисления. Полное число получаем, суммируя значения по разрядам. (Пример: в десятичном коде 11110, т =10; младший разряд - 1, второй - 10, третий - 100, то есть единица старшего разряда в десять раз больше единицы предыдущего разряда - единицы, десятки, сотни; также и в других системах счисления.) Чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а следовательно, и меньшее время для его передачи. Однако с ростом основания усложняются устройства передачи и приема сигналов, так как логические элементы в этом случае должны иметь большее число устойчивых состояний. Если учитывать оба эти обстоятельства, то целесообразно выбрать систему, обеспечивающую минимум произведения основания кода т на количество разрядов n для выражения любого числа. Найдем этот минимум по графику для большого числа 6000010. 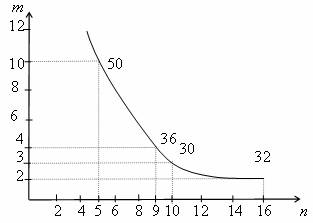 Рисунок 1. График зависимости числа разрядов п от основания кода т для числа 60000 Из графика следует, что наиболее эффективной системой является троичная. Незначительно уступают ей двоичная и четверичная. Системы с основанием десять и более значительно хуже. С точки зрения удобства физической реализации логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе. Действительно, арифметические операции в двоичной системе достаточно просты: сложение вычитание умножение 0+0=0; 0 - 0=0; 0·0=0; 0+1=1; 1 - 0=1; 0·1=1; 1+0=1; 1 - 1=0; 1·0=1; 1+1=10; 10 - 1=1 1·1=1 Сложение по модулю в двоичной системе также просто: 00=0; 01=1; 11=0; 10=1 Итак, для передачи и проведения логических и арифметических операций наиболее целесообразен двоичный код. Однако он неудобен при вводе и выводе информации, так как человеку трудно оперировать с непривычными двоичными числами. Кроме того, запись таких чисел на бумаге оказывается слишком громоздкой. Поэтому помимо двоичной получили распространение системы, которые, с одной стороны, легко сводятся как к двоичной, так и к десятичной системе, а с другой - дают более компактную запись. К таким системам относятся восьмеричная, шестнадцатеричная и двоично-десятичная. В восьмеричной системе для записи всех возможных чисел используется восемь цифр - от нуля до семи включительно. Перевод чисел из восьмеричной системы в двоичную крайне прост и сводится к замене каждой восьмеричной цифры равным ей трехразрядным двоичным числом. Например, для восьмеричного числа 745 получим: 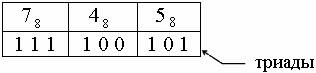 Поскольку в восьмеричной системе числа выражаются короче, чем в двоичной, она широко используется как вспомогательная система при программировании (особенно для микро- и мини-ЭВМ в машинных кодах). Чтобы сохранить преимущества двоичной системы, используют двоично-десятичные коды. В таком коде каждая цифра десятичного числа записывается в виде четырехразрядного двоичного числа. С помощью четырех разрядов можно образовать шестнадцать различных комбинаций, из которых любые десять могут составить двоично-десятичный код. Наиболее распространен код 8-4-2-1. Этот код относится к взвешенным кодам. Цифры в названии кода означают вес единиц в соответствующих двоичных разрядах. Он соответствует первым десяти комбинациям натурального двоичного кода (табл. 1). Таблица 1
Код 8-4-2-1 обычно используется как промежуточный при введении в вычислительную машину данных, представленных в десятичном коде. Перевод чисел из десятичного в двоично-десятичный код осуществляется перфоратором в процессе переноса информации на перфоленту или перфокарту. Последующее преобразование в двоичный код осуществляется по специальной программе в самой машине. Двоично-десятичные коды с весами 5-1-2-1 и 2-4-2-1 используются при поразрядном уравновешивании в цифровых измерительных приборах (цифровые вольтметры и т.п.). Недостатки взвешенных кодов: при передаче информации по каналам связи под действием помех отдельные элементы кода могут так исказиться, что будут приняты неверно. Например, вместо «0» будет принят элемент «1» или наоборот. Если будет искажен старший разряд, то ошибка будет значительно больше, чем при искажении младшего разряда. С этой точки зрения лучше применять невзвешенный код, у которого ошибки, вызванные помехами, были бы одинаковыми для любого разряда. В невзвешенных кодах позициям (разрядам) кодовой комбинации не приписывают определенных весов. Вес имеет лишь вся кодовая комбинация в совокупности. Рассмотрим невзвешенный двоичный рефлексный код Грея (табл. 2). Таблица 2
Правило получения кода Грея: кодовую комбинацию натурального двоичного кода складывают по модулю 2 с такой же комбинацией, сдвинутой на один разряд вправо, при этом младший разряд сдвинутой комбинации отбрасывается.  Характерные особенности кода Грея: 1) каждая последующая комбинация всегда отличается от предыдущей только в одной позиции (в одном разряде); 2) смена значений элементов в каждом разряде (1 на 0 или 0 на 1) при переходе от комбинации к комбинации в коде Грея происходит вдвое реже, чем в натуральном двоичном коде. Это свойство кода Грея позволяет получить точность кодирования выше по сравнению с натуральным двоичным кодом при том же быстродействии схемы кодирования; 3) при сложении двух соседних комбинаций кода Грея по модулю 2 (mod2) число единиц равно числу разрядов минус три (n-3). Это свойство кода Грея можно использовать для проверки правильности принятых комбинаций. В коде Грея можно выделить оси симметрии (оси отражения), относительно которых наблюдается идентичность элементов в некоторых разрядах. Так, например, имеет место симметрия относительно оси, проведенной между числами 7 и 8 (идентичны три символа младших разрядов). Эта особенность и послужила основанием для введения термина «рефлексный», то есть отраженный код. Рассмотренные свойства кода Грея показывают, что он удобен для аналого-цифрового преобразования различных непрерывных сообщений и их передачи по каналам связи (сервосистемы). Недостатком кода Грея и других рефлексных кодов является то, что эти коды невзвешенные, их трудно обрабатывать с помощью ЭВМ, так как сложнее выполнять декодирование. Преобразование кода Грея в натуральный двоичный код выполняется по правилу: старший разряд записывается без изменения, каждый следующий символ кода Грея нужно инвертировать, если в натуральном коде перед этим была получена «1», и оставить без изменения, если в натуральном коде был получен «0». (Пример: 910=1101гр =10012). Контрольные вопросы: Что такое триады? Что такое тетрады? Достоинства и недостатки взвещенных кодов. Характерные особенности кода Грея. Правила преобразования кода Грея. |
