Курсовой по Теоретическим Основам Электроники. Вотинцев. Введение расчёт цепей постоянного тока 2
 Скачать 322.61 Kb. Скачать 322.61 Kb.
|
 СодержаниеВВЕДЕНИЕ………………………………………………………...…………….1.Расчёт цепей постоянного тока 2 1.1.Расчет линейной электрической цепи 3 1.1.1.Составить по закону Кирхгофа систему уравнений для определения токов во всех ветвях схемы. 3 1.1.2.Методом контурных токов определить токи во всех ветвях схемы. 5 1.1.3.Составить баланс мощностей для заданной схемы 7 1.1.4.Построить потенциальную диаграмму для любого замкнутого контура, включающего ЭДС. 7 1.1.5.Результаты расчетов токов по п.п. 1.1.2 представить в виде таблицы. 8 1.2.Расчет нелинейной электрической цепи 8 1.2.1.Провести расчет графическим методом 9 1.2.2.Построить вольт-амперную характеристику 10 2.Расчет цепей переменного тока 11 2.1.Расчет однофазной электрической цепи(символическим методом) 11 2.1.1.Рассчитать реактивные сопротивления элементов цепи 11 2.1.2.Начертить схему замещения электрической цепи 11 2.1.3.Определить действующие значения токов во всех ветвях цепи 12 2.1.4.Записать уравнение действующего значения тока источника 13 2.1.5.Составить баланс активных и реактивных мощностей 13 2.1.6.Потсроить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений 14 2.2Расчет трехфазной электрической цепи(в комплексной форме) 15 2.2.1.Начертить схему соединения сопротивлений 15 2.2.2.Определить фазные токи 15 2.2.3.Определить линейные токи 16 2.2.4.Определить ток в нулевом проводе 16 2.2.5.Определить активную, реактивную и полную мощность каждой фазы 16 2.2.6.Определить угол сдвига фаз между током и напряжением каждой фазы 17 Введение Дисциплина “ Теоретические основы электротехники” является одной из базовых технических дисциплин специальности 2-36 03-31 «Монтаж и эксплуатация электрооборудования» (по направлениям), направления специальности 2-36 03-31-01 «Монтаж и эксплуатация электрооборудования (производственная деятельность)», 2-36 03-31-01 01 «Монтаж и эксплуатация электрооборудования предприятий и гражданских зданий» и ориентирована на овладение учащимися знаниями в области электротехники. Умения применять эти знания для решения практических задач в данной области, а так же на формирование следующих компетенций: 1.способности к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения; 2.готовности выявить естественную, научную сущность проблем, возникающих в ходе профессиональной деятельности, и способности привлечь для их решения соответствующие физико-математические умения и навыки; 3. способности использовать методы анализа и моделирования линейных и нелинейных электрических цепей постоянного и переменного тока; 4.способности к самостоятельному обучению, получению знаний по направлению специальности в области научных исследований. Изучение учебной дисциплины "Теоретические основы электротехники" заканчивается закреплением теоретических и практических знаний и навыков при курсовом проектировании. Я выполнил курсовой проект в соответствии с индивидуальным заданием (вариантом темы) и методическими требованиями. Результаты расчетов изложены в пояснительной записке. Объем курсового проекта составляет 19 страниц печатного текста. Графики, ВАХ, векторные и потенциальные диаграммы вычерчены на миллиметровой бумаге формата А-4, пояснительная записка выполнена на листах писчей бумаги формата А 4, сброшюрированных в папку. Оформлен курсовой проект согласно методическим рекомендациям. 1.Расчёт цепей постоянного тока Основная цель расчёта электрической цепи заключается в определении токов в её ветвях. Зная токи, нетрудно найти напряжения и мощности ветвей и отдельных элементов цепи. Величины токов, напряжений, мощностей дают возможность оценить условия и эффективность работы электротехнического оборудования и приборов во всех участках электрической цепи. Связь между ЭДС, напряжениями и токами линейных электрических цепей выражается линейными уравнениями, т.е. уравнениями первой степени, поэтому для расчёта их применяются аналитические методы с обычными алгебраическими преобразованиями. 1.1.Расчет линейной электрической цепи Электрическая схема постоянного тока представлена на рисунке 1. Параметры сложной электрической цепи постоянного тока приведены в таблице 1. Рисунок 1.1.1 Схема электрическая 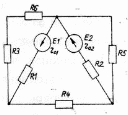 Данные для расчета приведены в таблице 1 Таблица 1 - Параметры электрической цепи
1.1.1.Составить по закону Кирхгофа систему уравнений для определения токов во всех ветвях схемы. Метод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи. При расчете данным методом произвольно задаем направление токов в ветвях I1, I2, I3, I4, I5. Составляем систему уравнений. В заданной цепи шесть ветвей, значит, в системе должно быть шесть уравнений (m = ). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с п узлами можно составить (п - 1) независимых уравнений. В нашей цепи четыре узла (А, В, С), значит, число уравнении п -1 = 3-1 = 2. Составляем три уравнения для любых 2-х узлов, например, для узлов А, С. узел А: I1=I4+I3 узел С: I2=I3+I4 Всего в системе должно быть пять уравнений. Два уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие. Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа. Контур ABC - обход против часовой стрелки: E2+E1 =I1( r01+R1 )+IR4+I2(R2+r02) Контур AB- обход по часовой стрелки: Е1 =I1(R1+r01)+I3R3+I6R6 Контур BC— обход по часовой стрелке: E2=I2(R2+r02)+I5R5 ЭДС в контуре берется со знаком «+» если направление ЭДС совпадает с обходом контура, если не совпадает – знак «-» Падение напряжения на сопротивлении контура берется со знаком «+», если направление тока в нем совпадает с обходом контура, со знаком «-», если не совпадает. 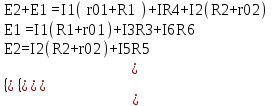 Решив систему, определим величину и направление тока во всех ветвях схемы. Если при решении системы ток получается со знаком значит его действительное направление обратно тому направлению, которым мы задались. 1.1.2.Методом контурных токов определить токи во всех ветвях схемы.Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на п-1. Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока — контурного тока, являющегося расчетной величиной. Итак, в заданной цепи (рис. 1) можно рассмотреть три контура-ячейки (АBC, AB, BC) и ввести для них контурные токи Ik1, Ik2, Ik3. Контуры-ячейки имеют ветвь, не входящую в другие контуры - это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей. Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления. При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур - ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим: —Cтрелками указываем выбранные направления контурных токов в контурах - ячейках. Направление обхода контуров принимаем таким же; —Cоставляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей. 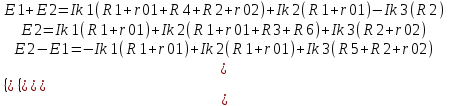 Подставляем в уравнение численные значения ЭДС и сопротивлений 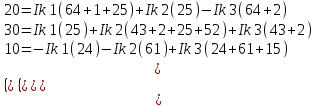 Или 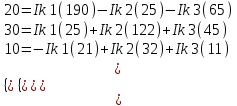 Решим систему с помощью определителей. Вычислим определитель системы ∆, и частные определители ∆1, ∆2, ∆3. ∆= 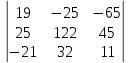 =777650 =777650∆1= 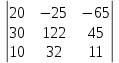 =186940 =186940∆2= 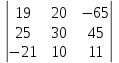 =127600 =127600∆3= 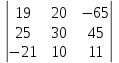 =68640 =68640Вычисляем контурные токи ветвей: Ik1= 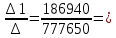 0.24(A) 0.24(A)Ik2= 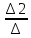 = =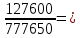 0.164 (A) 0.164 (A)Ik3= 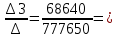 0.088 (A) 0.088 (A)Действительные токи ветвей I1=Ik1-Ik23=0.152(A); I2=Ik2+Ik3=0.252(A); I3=Ik3=0.088(A); I4=Ik1+Ik2=0.404(A) I5=Ik2=0.164(A) I6=Ik3=0.15(A) 1.1.3.Составить баланс мощностей для заданной схемы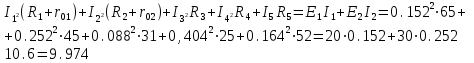 Баланс мощностей сошелся. 1.1.4.Построить потенциальную диаграмму для любого замкнутого контура, включающего ЭДС.Рисунок 1.1.2 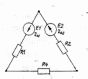 Возьмем контур БСГЕЗК. Зададимся обходом контура по часовой стрелке. Заземлим одну из точек контура, пусть это будет точка А. Потенциал этой точки равен нулю φA=0 (рис. 1.2 ). Зная величину и направление токов ветвей и ЭДС, а также величины сопротивлений, вычислим потенциалы всех точек контура при переходе от элемента к элементу. Начнем обход от точки c. 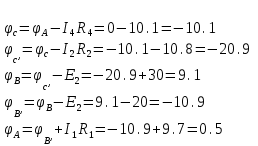 0 - проверочная точка. Строим потенциальную диаграмму. По оси абсцисс откладываем сопротивления контура в той последовательности, которой производим обход контура, прикладывая сопротивления друг к другу, во оси ординат - потенциалы точек с учетом их знака. 1.1.5.Результаты расчетов токов по п.п. 1.1.2 представить в виде таблицы.
1.2.Расчет нелинейной электрической цепи1.2.1.Провести расчет графическим методомР 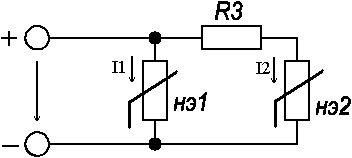 исунок 1.2.1 исунок 1.2.1Дано: U=160 В; R3=40 Ом; Определить: I1;I2;I3;U1;U2;U3.  Расчет цепи производим графическим методом. Для этого в общей системе координат строим вольтамперные характеристики (ВАХ) линейного и нелинейных элементов: ВАХ линейного элемента строим по уравнению . Она представляет собой прямую, проходящую через начало координат. Для определения координаты второй точки ВАХ линейного элемента задаемся произвольным значением напряжения. Например, UR = 640 В, тогда соответствующее значение тока 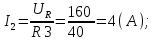 Соединив полученную точку с началом координат, получим ВАХ линейного элемента. Далее строится общая ВАХ цепи с учетом схемы соединения элементов. В нашей цепи соединение элементов смешанное. Поэтому графически "сворачиваем" цепь. Начинаем с разветвленного участка. Нелинейный элемент нэ1 и нелинейный элемент нэ2 соединены последовательно. Задаемся током и складываем напряжения при этом токе. С учетом этого строим общую для них ВАХ. Точка пересечений этих значений тока и напряжения даёт одну из точек их общей ВАХ. В результате получаем множество точек и по ним строим ВАХ . Дальнейший расчет цепи производим по полученным графикам. Строим для них общую ВАХ. В данном случае задаёмся напряжением и складываем токи. Проделываем это многократно. По полученным токам строим общую ВАХ цепи . Чтобы найти токи и напряжения на всех элементах цепи, поступаем так: по оси напряжений находим значения напряжения, равное 160В (точка «а»). Из этой точки восстанавливаем перпендикуляр до пересечения с общей ВАХ , получим точку «b». Из точки «b» опускаем перпендикуляр на ось тока (точка «с»). 1.2.2.Построить вольт-амперную характеристику 2.Расчет цепей переменного тока2.1.Расчет однофазной электрической цепи(символическим методом)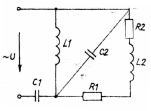 Дано: Um=54 B; ψu=60 град; R1=10 Ом; R2=20 Ом: L1=31,8 млГн; L2=50,9 млГн; С1=318 мкФ; С2=318 мкФ; Определить: XL1; XL2; Xc1; Xc2; I; I1; I2; I3; I4; I5; i. 2.1.1.Рассчитать реактивные сопротивления элементов цепи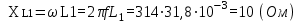 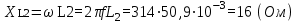 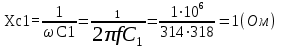 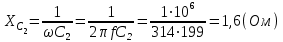 2.1.2.Начертить схему замещения электрической цепи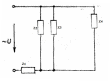 Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи: 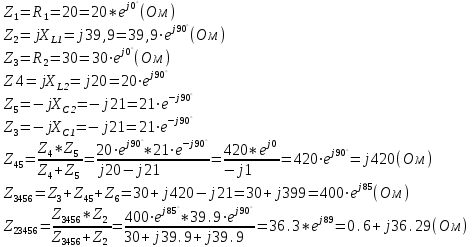 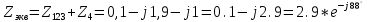 Выразим действующее значение напряжений в комплексной форме: 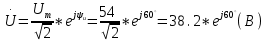 2.1.3.Определить действующие значения токов во всех ветвях цепиВычисляем токи ветвей и общий ток цепи: 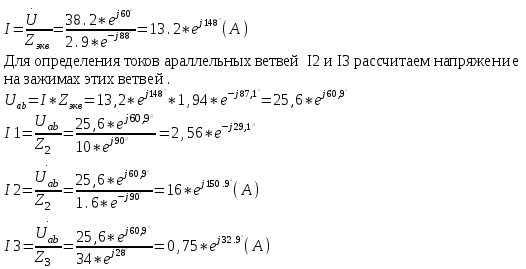 2.1.4.Записать уравнение действующего значения тока источника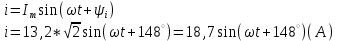 2.1.5.Составить баланс активных и реактивных мощностейКомплексная мощность цепи: 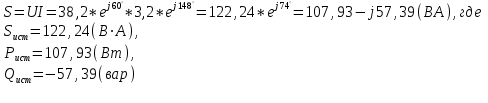 Активная Рпр и Qпр реактивная мощность приемников: 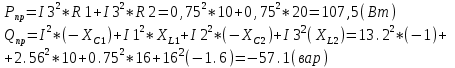   Баланс мощностей выполняется: 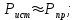 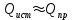 2.1.6.Потсроить векторную диаграмму токов, совмещенную с топографической векторной диаграммой напряжений2.2Расчет трехфазной электрической цепи(в комплексной форме)2.2.1.Начертить схему соединения сопротивленийВ цепи, изображенной на схеме, потребители соединены треугольником. Известно линейное напряжение Uл=38(В) и сопротивления фаз Rab = 1,88(Ом); ХLab = 0,68(Ом); RBC =3,8(Ом) XCbc =2.2 (Ом) RCA = 3,1(Ом); XLca=2,57(Ом). Определить фазные, линейные токи, мощности активные, реактивные, полные мощности каждой фазы и всей цепи. Построить векторную диаграмму цепи. Д 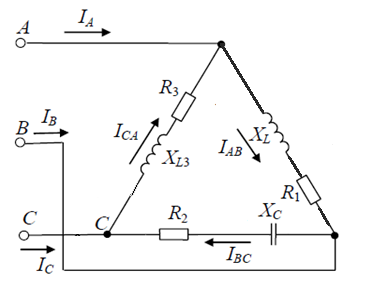 ано: Rab=1,88(Ом); Rbc=3,8 Rca=3,1(Ом); XLab=0,68(Ом); XLca=2.57(Ом); XCbc=2.2(Ом); Uл=38(В). ано: Rab=1,88(Ом); Rbc=3,8 Rca=3,1(Ом); XLab=0,68(Ом); XLca=2.57(Ом); XCbc=2.2(Ом); Uл=38(В).Определить: IA; IB; IC; Iab; Ibc; Ica; Pab; Pbc; Pca; P; Qab; Qbc; Qca; Q; Sab; Sbc; Sca; S. 2.2.2.Определить фазные токиМодули фазных напряжений при соединении треугольником равны линейным напряжениям  Uл=Uф=38(В), то есть Uab=Ubc=Uca=38(B). Uл=Uф=38(В), то есть Uab=Ubc=Uca=38(B).Комплексы данных напряжений запишем из условия, что вектор 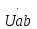 совмещен с действительной осью комплексной плоскости совмещен с действительной осью комплексной плоскости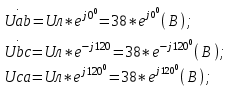 Вычислим комплексы фазных сопротивлений: 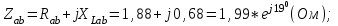 где 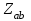 =1,99(Ом), φ =1,99(Ом), φ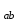 = =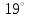 ; ;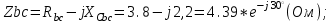 где Zbc=4.39(Ом), 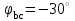 где Zca=4.02(Ом), 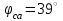 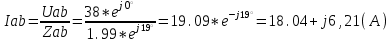 Модуль Iab=19.09(A), ψab= -19° 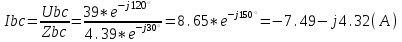 Модуль Ibc=8.65(A), ψbc= -150° 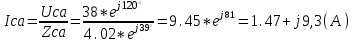 Модуль Ica=9.45, ψ=81° 2.2.3.Определить линейные токиНаходим линейные токи из уравнений, записанных по первому закону Кирхгофа для узлов А, B, C IA=Iab-Ica=18.04+j6.21+1.47-j9.33=24.25-j7,86=25.49* 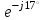 (A); (A);IB=Ibc-Iab=-7.49-j4.32-18.04-j6.21=-11.81-j11.83=16.71* 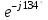 (A); (A);IC=Ica-Ibc=1.47+j9.3+7.49+4.32=10.8+j11.81=16* 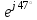 (A); (A);2.2.4.Определить ток в нулевом проводеУ нас дано соединение треугольником. Таким образом нулевой провод отсутствует. 2.2.5.Определить активную, реактивную и полную мощность каждой фазы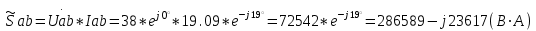 где Sab=72542(B·A), Pab=286589(Bт), Qab= -23617(вар) где Sab=72542(B·A), Pab=286589(Bт), Qab= -23617(вар)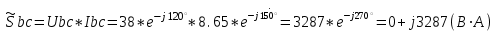 где Sbc=3287(B·A); Pbc= 0(Вт); Qbc=3287(вар) где Sbc=3287(B·A); Pbc= 0(Вт); Qbc=3287(вар) 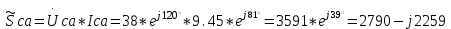 где Sca=3591(В·А); Pca= 2790(Вт); Qca=-2259(вар) 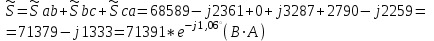 где S=71391(B·A); P=71379(Вт); Q= -1333(вар) 2.2.6.Определить угол сдвига фаз между током и напряжением каждой фазы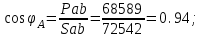 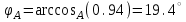 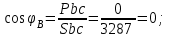 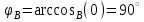 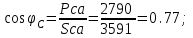 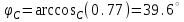 Заключение В этом курсовом проекте, мы рассмотрели вопросы: 1. Расчёт цепей постоянного тока: 1) Расчет линейной электрической цепи; 2) Расчет нелинейной электрической цепи. 2. Расчет цепей переменного тока: 1) Расчет однофазной электрической цепи (символическим методом); 2) Расчет трехфазной электрической цепи (в комплексной форме). Научились рассчитывать токи в цепях с постоянным и переменным током. Научились составлять баланс мощностей и векторные диаграммы схем. А также научились находить мощности в цепи. При выполнении курсового проекта мы закрепили теоретические знания и практические и навыки при решении задач и расчете цепей постоянного и переменного тока с построением потенциальных и векторных диаграмм. Список литературы Атабеков Г. И. - Теоретические основы электротехники. Линейные электрические цепи. Изд. Лань, 2009. 592 с.[электронный ресурс] Бобровников Л. 3., Электротехника: учебник для вузов Л. 3. Бобровников.- 5-е издание, перераб. и доп,- СПБ.: Питер, 2004. - 560 с.:ил.-Мо Бычков Ю. А., Золотницкий В. М., Чернышев Э. П. Основы теории электрических цепей. Лань, 2002. 464 с.4. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. - М.: Высшая школа, 2000. Гилицкая Л.Н. Теоретические основы электротехники. Курсовое проектирование. Минск 1997. |
