|
|
гр. графы. Введение в теорию графов
Введение в теорию графов
Теория графов представляет собой раздел математики, имеющий широкое практическое применение во многих областях человеческой деятельности. Математика, физика, химия, теория связи, электротехника, архитектура, исследование операций, генетика, психология – вот далеко не полный список областей ее применения
Теория графов становится одной из существенных частей математического аппарата кибернетики, языком дискретной математики.
Граф G задается с помощью пары множеств G = (V, R), где V есть множество вершин, а R – множество линий, соединяющих пары вершин. Линии со стрелками называются дугами, без стрелок – ребрами. Обычно граф представляют с помощью схемы, на которой некоторые вершины соединены ребрами (дугами).
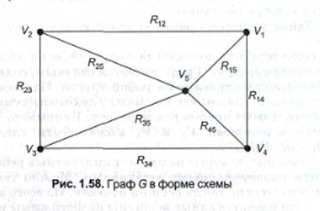
Вершинами могут служить объекты любой природы: будь то населенные пункты, компьютерные сети, элементы блок- схем алгоритмов. Под ребром могут подразумеваться дороги между соседними городами, линии связи между компьютерами.
Вершины называются смежными, если их соединяет ребро. Например, на рис. смежные вершины V1 и V2 , так как их соединяет ребро R12 .
Множество V, R являются конечными – мы можем перечислить все вершины и ребра графа. Количество вершин и количество ребер графа определяют мощности множеств V и R. Так, количество вершин графа G ровно 5, а количество ребер равно 8.
Ребро и любая из его двух вершин называются инцидентными. Под степенью вершин подразумевается количество инцидентных ей ребер. Так, степень вершин V1 равно 3, а степень вершин V5 равна 4.
Последовательность чередующихся ребер и вершин графа называется маршрутом. В графах можно выделить различные маршруты. Маршрут называется замкнутым, если вершины начала и конца маршрута совпадают. Если ребра и вершины, образующие маршрут различны, то такой маршрут называется цепью. Путь в ориентированном графе — это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.
Длина маршрута равна количеству ребер, входящих в него.
Граф называется связным, если любые две его вершины можно соединить маршрутом (или путем).
Ориентированные графы.
Граф, в котором направление линий принципиально называется ориентированным (орграф). В орграфе каждое ребро имеет одно направление. Такие ребра называются дугами. Для орграфа вводятся такие понятия, как входящая и исходящая степени вершины. Это соответственно число входящих в вершину дуг и число исходящих из нее дуг.
Взвешенные графы.
Взвешенный граф – это граф, в котором с вершинами и линиями связана некоторая дополнительная информация. Эта информация называется весом вершины или линии. Вес позволяет отобразить на графе не только структуру системы, но и различные свойства компонент или связей, количественная характеристика. Вес сети равен сумме весов ее ребер.
Полный граф
Граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром. В полном графе каждая его вершина принадлежит одному и тому же числу ребер. Для задания полного графа достаточно знать число его вершин. Полный граф с n вершинами обычно обозначается через Kn.
Граф, не являющийся полным, можно преобразовать в полный с теми же вершинами, добавив недостающие ребра. Вершины графа G и ребра, которые добавлены, тоже образуют граф. Такой граф называют дополнением графа и обозначают его G .
Двудольный граф
Допустим, что множество вершин графа можно разбить на два непересекающихся подмножества V1 и V2 , так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-либо вершиной из V2 , тогда G называем двудольным графом. Такие графы иногда обозначают G(V1, V2 ) , если хотят выделить два указанных подмножества. Двудольный граф можно определить и по-другому: в терминах раскраски его вершин двумя цветами, скажем, красным и синим. При этом граф называется двудольным, если каждую его вершину можно окрасить красным или синим цветом так, чтобы любое ребро имело один конец красный, а другой — синий. Следует подчеркнуть, что в двудольном графе совсем не обязательно каждая вершина из V1 соединена с каждой вершиной из V2 ; если же это так и если при этом граф G простой, то он называется полным двудольным графом и обычно обозначается Km,n , где m, n — число вершин соответственно в V1 и V2 .
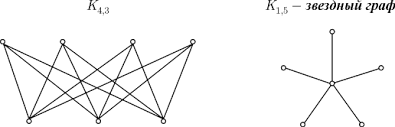
Заметим, что граф Km,n имеет ровно m + n вершин и m*n ребер.
Плоский граф
Плоским графом называется граф, изображенный на плоскости так, что никакие два его ребра (или, вернее, представляющие их кривые) геометрически не пересекаются нигде, кроме инцидентной им обоим вершины. Граф, изоморфный плоскому графу, называется планарным. Планарный граф можно определить еще так: граф планарен, если его можно уложить на плоскости. Рисунок графа, в котором никакие два его ребра не пересекаются, если не считать точками пересечения общие вершины, называют плоским представлением графа. Ясно, что плоское представление имеет только плоский граф. Обратно, у всякого плоского графа непременно найдется плоское представление. Плоские графы — это простые циклы, деревья, лес, а также граф, содержащий цикл, из вершин которого "выходят" деревья.
Примером неплоского графа может служить полный граф с пятью вершинами. Любые попытки начертить его плоское представление обернутся неудачей.
В качестве характеристики плоского представления графа вводится понятие грани. Гранью в плоском представлении графа G называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.
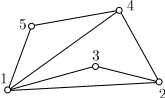
На рисунке показано плоское представление графа G с тремя гранями: (1, 5,4,1), (1, 3, 2,4,1), (1,2,3,1). Часть плоскости, ограниченная простым циклом (1,2,4,1), гранью не является, так как содержит цикл (1, 2, 3,1). Простой цикл, ограничивающий грань, называется границей грани. Две грани будем называть соседними, если их границы имеют хотя бы одно общее ребро.
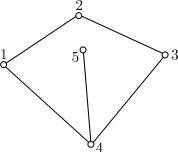
В данном графе часть плоскости, ограниченная простым циклом (1,2,3,4,1), является гранью, так как ребро (4,5), расположенное внутри грани, не образует цикла.
Не является гранью заштрихованная часть плоскости в данном примере, так как она содержит цикл, да к тому же эта часть плоскости не ограничена циклом. Ребро (1,2) является мостом, соединяющим циклы. Такие мосты называются перегородками.
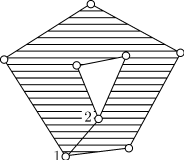
В качестве грани можно рассматривать и часть плоскости, расположенную "вне" плоского представления графа. Она ограничена "изнутри" простым циклом и не содержит других циклов. Эту часть плоскости называют бесконечной гранью.
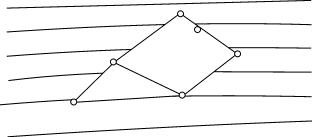
На рисунке часть бесконечной грани заштрихована. Всякое плоское представление графа либо не имеет бесконечной грани, либо имеет в точности одну бесконечную грань. Как особый случай вводится бесконечная грань в плоском представлении дерева и леса. В плоском представлении дерева и леса за грань принимают всю плоскость рисунка.
Элементарным стягиванием называется такая процедура: берем ребро е (вместе с инцидентными ему вершинами, например, V и W) и"стягиваем" его, то есть удаляем е и отождествляем V и W. Полученная при этом вершина инцидентна тем ребрам (отличным от е ), которым первоначально были инцидентны V или W.
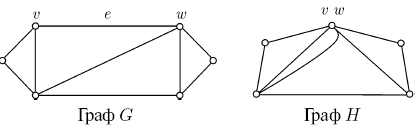
Граф G называется стягиваемым к графу Н, если Н можно получить из G с помощью некоторой последовательности элементарных стягиваний.
Граф планарен тогда и только тогда, если он не содержит подграфов, стягиваемых в К5 или к Кз.з.
Формула Эйлера
Для всякого плоского представления связного плоского графа без перегородок число вершин (V), число ребер (Е) и число граней с учетом бесконечной (R) связаны соотношением V –Е + R = 2.
Пусть граф G — связный, плоский граф без перегородок. Определим значение алгебраической суммы V –Е + R для его произвольного плоского представления.
Преобразуем данный граф в дерево, содержащее все его вершины. Для этого удалим некоторые ребра графа G, разрывая поочередно все его простые циклы, причем так, чтобы граф оставался связным и без перегородок.
Заметим, что при таком удалении одного ребра число граней уменьшается на 1, так как при этом либо пропадет один простой цикл, либо два простых цикла преобразуются в один. Следовательно, значение разности Е - R при этом остается неизменным.
На рисунке ребра, которые мы удаляем, изображены кривыми. В полученном дереве обозначим число вершин — Vd , число ребер — Ed, число граней — Rd . Справедливо равенство Е — R = Ed — Rd.
В дереве одна грань, то есть Е - R = Ed - 1. Операция удаления ребер из графа не меняет число его вершин, то есть V = Vd. По теореме в дереве Vd - Ed = 1. Отсюда V - Ed = 1, то есть Ed = V - 1, а потому Е-R = V - 2 или V - Е + R = 2.
Итак, доказано, что если в плоском представлении связного графа без перегородок V вершин, Е ребер и R граней, то V - Е + R = 2. Полученная формула называется формулой Эйлера.
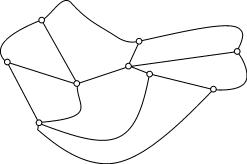
Триангулированный граф
Рассмотрим плоский граф G с пятью вершинами.
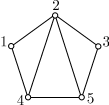
Если добавить к нему ребра (1, 3) и (1,5) и, то полученный новый граф G тоже будет плоским.
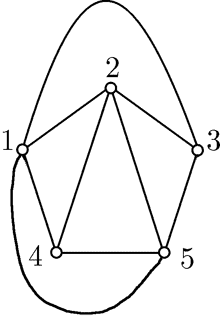
К этому графу не удается добавить ни одного ребра так, чтобы новый граф тоже был плоским.
Плоский граф называется максимально плоским, если невозможно добавить к нему ни одного ребра так, чтобы полученный граф был плоским. Изображенный граф является максимально плоским.
Каждая грань в плоском представлении максимально плоского графа имеет 3 вершины. Поэтому максимально плоский граф называют триангулированным. Операция добавления новых ребер, в результате которой в плоском представлении каждая грань имеет ровно 3 вершины, называется триангуляцией графа.
|
Примеры решения задач.
Задача 1
На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?
Решение
Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем: Г = Б + В Д = Г + В Ж = Б + Г Е = Ж + Г + Д Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.
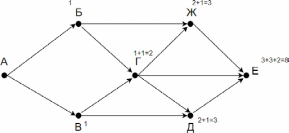
Задача 2
На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому.
Решение:
Вершины графа - это деревья, обозначенный первой буквой названия дерева. В данной задача два отношения: “быть ниже” и “быть выше”. Рассмотрим отношение “быть ниже” и проведем стрелки от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь.

Задача 3
Под рукой есть 6 видов овощей (капуста, морковь, лук, помидоры, огурцы и перец). Для салата нужно 3 вида овощей. Сколько всего различных салатов можно приготовить?
Решение
Построим полный граф.
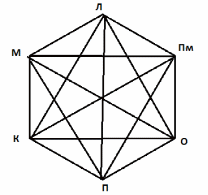
Каждые три овоща на полном графе образуют треугольник.
Например, капуста образует треугольники с оставшимися 5 овощами. Таких треугольников 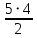 =10, где деление на 2 учитывает повторение ребра в каждой паре («лук-огурец» = «огурец-лук» и т.д.). =10, где деление на 2 учитывает повторение ребра в каждой паре («лук-огурец» = «огурец-лук» и т.д.).
Количество треугольников, в которые не входит капуста: 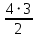 =6 =6
Количество треугольников, в которые не входят капуста и морковь: 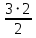 =3 =3
Количество треугольников, в которые не входят капуста, морковь и перец: 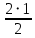 =1 =1
Итого 10+6+3+1 = 20 различных треугольников.
Ответ: 20 салатов |
|
|
 Скачать 152.48 Kb.
Скачать 152.48 Kb.


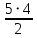 =10, где деление на 2 учитывает повторение ребра в каждой паре («лук-огурец» = «огурец-лук» и т.д.).
=10, где деление на 2 учитывает повторение ребра в каждой паре («лук-огурец» = «огурец-лук» и т.д.).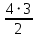 =6
=6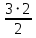 =3
=3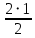 =1
=1










