|
|
КР по мат. логике Трипузова Карина Дмитриевна, МО 3.031.1.18. Контрольная работа по математической логике для студентов по мо озо 6 семестр (20202021 уч г.)
Контрольная работа по математической логике для студентов
ПО МО ОЗО 6 семестр (2020-2021 уч.г.)
Составитель С.И. Плаксин
Задание 1. Найдите соответствующую форму 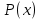 для каждого множества: для каждого множества:
а) {2, 3, 5, 7, 11, 13, 17, 19};
б) {м, о, н, е, ж, т, с, в};
в) [-3, 4].
Решение:
а) 
б)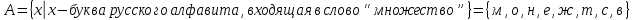
в)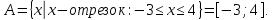
Задание 2. С помощью математической индукции докажите, что если конечное множество А содержит 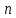 элементов, то множество-степень элементов, то множество-степень 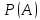 содержит содержит 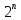 элементов. элементов.
Доказательство.
Множество, состоящее из одного элемента a, имеет два (т.е. 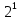 ) подмножества: ∅ и {a}. ) подмножества: ∅ и {a}.
Множество, состоящее из двух элементов a и b, имеет четыре (т.е.  ) подмножества: ∅, {a}, {b}, {b; a}. ) подмножества: ∅, {a}, {b}, {b; a}.
Множество, состоящее из трех элементов a, b, c имеет восемь (т.е. 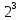 ) подмножества: ∅, {a}, {b}, {b; a}, {c}, {c; a},{c; b},{c; b; a}. ) подмножества: ∅, {a}, {b}, {b; a}, {c}, {c; a},{c; b},{c; b; a}.
Ясно, что добавление нового элемента удваивает число подмножества.
Завершим доказательство применением метода математической индукции. Сущность этого метода в том, что если утверждение (свойство) справедливо для некоторого начального натурального числа  и если из предположения, что оно справедливо для произвольного и если из предположения, что оно справедливо для произвольного  , можно доказать его справедливость для числа k + 1, то это свойство справедливо для всех натуральных чисел , можно доказать его справедливость для числа k + 1, то это свойство справедливо для всех натуральных чисел 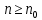 . .
1. Для n = 1 (и даже для n = 2, 3) теорема доказана.
2. Допустим, что теорема доказана для n = k, т.е. число подмножеств множества, состоящего из k элементов, равно 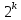 . .
Докажем, что число подмножеств множества B, состоящего из n = k + 1 элемента, равно 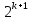 . .
Выбираем некоторый элемент b множества B. Рассмотрим множество A = B\{b}. Оно содержит k элементов. Все подмножества множества A – это подмножества множества B, не содержащие элемент b и, по предположению, их 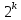 штук. Подмножеств множества B, содержащих элемент b, столько же, т.е. штук. Подмножеств множества B, содержащих элемент b, столько же, т.е. 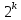 штук (по предыдущей задаче). Следовательно, всех штук (по предыдущей задаче). Следовательно, всех
подмножеств множества 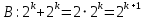 штук. Теорема доказана. штук. Теорема доказана.
Задание 3. Докажите, что отношение делимости на множестве натуральных чисел является отношением частичного порядка. Является ли это отношение линейным порядком? Является ли отношением частичного порядка отношение делимости на множестве целых чисел?
Решение:
1) Бинарное отношение R на множестве X называется отношением частичного порядка, если оно обладает следующими свойствами:
Рефлексивность: ∀a∈X:aRa.
Антисимметричность: ∀a,b∈X: если aRb и bRa, то a=b.
Транзитивность: ∀a,b,c∈X: если aRb и bRc, то aRc. Проверим, что отношение делимости на множестве натуральных чисел является отношением частичного порядка. Отношение делимости на множестве N определяется следующим образом: x делит y (или y делится на x), если существует такое целое k, что xk=y. Это отношение обозначается так: x|y .
Отношение делимости рефлексивно, так как для любого натурального x справедливо равенство x=x*1. Та как  , то, по определению отношения делимости x|x. , то, по определению отношения делимости x|x.
Отношение делимости антисимметрично, т.е. если x|y и y|x, то  . Докажем от противного. Предположим, что x . Докажем от противного. Предположим, что x y. По теореме: делитель y данного числа x не превышает этого числа, т.е. если x|y, то y y. По теореме: делитель y данного числа x не превышает этого числа, т.е. если x|y, то y x. Неравенства x. Неравенства  и и 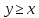 будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следовательно, наше предположение неверное и отношение делимости антисимметрично. будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следовательно, наше предположение неверное и отношение делимости антисимметрично.
Отношение делимости транзитивно, т.е. если x|y и y|z, то x|z.
Доказательство. Так как x|y, то существует такое натуральное число q, что x= yq, а так как y|z, то существует такое натуральное число р, что y = zр. Но тогда имеем: x = yq = (zp)q = z(pq). Число pq - натуральное. Значит, по определению отношения делимости, x|z.
Является ли это отношение линейным порядком? Ответ: нет - так как.
Бинарное отношение R на множестве X называется отношением линейного порядка, если оно является отношением частичного порядка и обладает следующим свойством: ∀a∈X ∀b∈X либо aRb, либо bRa.
 . Контрпример 5 и 6 . Контрпример 5 и 6 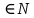 , но 5 не делит 6 и 6 не делит 5. , но 5 не делит 6 и 6 не делит 5.
Является ли отношением частичного порядка отношение делимости на множестве целых чисел? Ответ нет. Так как от ношением частичного порядка — не выполнена антисимметричность: 1|–1 и –1|1.
Задание 4. Пусть А={1, 2, 3}. На множестве 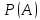 задано бинарное отношение задано бинарное отношение  : :  тогда и только тогда, когда множества тогда и только тогда, когда множества 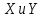 имеют равное количество элементов. Докажите, что это отношение является отношением эквивалентности и найдите классы эквивалентности. имеют равное количество элементов. Докажите, что это отношение является отношением эквивалентности и найдите классы эквивалентности.
Решение:
Рефлексивность: X ρ X для любого подмножества A. Симметричность: X ρ Y ⇔ «множества X и Y имеют равное количество элементов» ⇔ YρX. Транзитивность: XρYи YρZ ⇔ «множества X и Y имеют равное количество элементов» и «множества Z и Y имеют равное количество элементов» ⇒ «множества X и Z имеют равное количество элементов» ⇒ X ρ Z.
Классы эквивалентности: {A}, {{1, 2}, {2, 3}, {3, 1}}, {{1}, {2}, {3}}, ∅.
Логика высказываний
Задание 5. Ввести простые высказывательные переменные и составить формулы следующих составных высказываний:
а) Для устойчивого развития общества необходимы экономическая и политическая стабильность в стране;
Решение a):
A={ экономическая стабильность в стране}
B={ политическая стабильность в стране }
C={ устойчивого развития общества }
Формула:  . .
б) Неверно, что команда А станет чемпионом только при условии, что в финал чемпионата не выйдет ни одна из команд В, С или D;
Решение б): A={ команда А станет чемпионом }
B={ команда B станет чемпионом }
C={ команда C станет чемпионом }
D={ команда D станет чемпионом }
Формула: 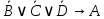 . .
в) Если в задаче ход решения неправильный или получен неверный ответ, то задача не засчитывается;
Решение в): A={ задаче ход решения неправильный }
B={ получен неверный ответ }
C={ задача не засчитывается }
Формула: 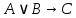 . .
г) Высказывания А и В одновременно верны или одновременно ложны тогда и только тогда, когда из высказывания А следует справедливость высказывания С;
Решение г): X={ высказывания А и В одновременно верны }
Y={ высказывания А и В одновременно ложны }
Z={ из высказывания А следует справедливость высказывания С }
Формула: 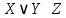 . .
д) Если параметр уравнения 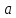 равен 0 или 1, то уравнение не имеет действительных решений. равен 0 или 1, то уравнение не имеет действительных решений.
Решение: X={ a=0 }
Y={ a=1 }
Z={уравнение не имеет действительных решений.}
Формула:  . .
Задание 6. Что можно сказать об истинностном значении высказывания
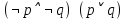 , если , если 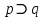 ложно? ложно?
Решение: Из того, что P ⊃ Q ложно, получаем P = И, Q = Л. Подставляем эти истинностные значения вместо P и Q в искомую формулу (¬P & ¬Q) (P ∨ Q) и получаем (¬И & ¬Л) (И ∨ Л) = (Л & И) И = Л И = Л. Следовательно, формула (¬P & ¬Q) (P ∨ Q) ложна.
Задание 7. Доказать, что отношение равносильности  формул ( формул (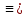 есть отношение эквивалентности, т.е. оно рефлексивно – для любой формулы А есть отношение эквивалентности, т.е. оно рефлексивно – для любой формулы А
А  ; симметрично – для любых формул А и В, если А ; симметрично – для любых формул А и В, если А  , то В , то В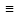 А; транзитивно – для любых формул А, В, С, если А А; транзитивно – для любых формул А, В, С, если А  и В и В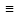 С, то А С, то А  . .
Доказательство: Рефлексивность следует непосредственно из тавтологии теоремы: Две формулы F и H алгебры высказываний равносильны тогда и только тогда, когда формула F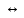 H является тавтологией: F H является тавтологией: F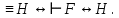
Для доказательства симметричности отношения 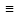 предположим, что А предположим, что А  , т.е. на основании признака равносильности А , т.е. на основании признака равносильности А 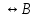 Тогда по тавтологии заключаем: формула B Тогда по тавтологии заключаем: формула B 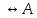 принимает всегда те же самые значения, что и формула принимает всегда те же самые значения, что и формула  , т.е. только истинные значения. Следовательно, А , т.е. только истинные значения. Следовательно, А  или (по признаку равносильности) B или (по признаку равносильности) B  . Симметричность доказана. . Симметричность доказана.
Если А  и B и B 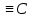 , т.е. , т.е. 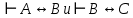 , то на основании определения конъюнкции заключаем, что: , то на основании определения конъюнкции заключаем, что: 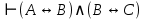 . Привлекая теперь тавтологию и правило заключения для получения тавтологий, получаем . Привлекая теперь тавтологию и правило заключения для получения тавтологий, получаем 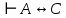 , или A , или A 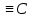 . Следовательно, отношение . Следовательно, отношение 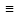 транзитивно. транзитивно.
Задание 8. Доказать, что формулы А и В равносильны (А  тогда и только тогда, когда эквиваленция формул А тогда и только тогда, когда эквиваленция формул А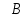 тождественно истинна. тождественно истинна.
Решение: Необходимость. Пусть А и В равносильны. Тогда по определению связки ≡ форма А≡В всегда принимает значение И, т.е. является тавтологией.
Достаточность. Пусть А≡.В тавтология, т.е. принимает всегда значение И. Это означает, что А и В имеют всегда одинаковые истинностные значения, т.е. они равносильны. Теорема доказана.
Задание 9. Какие из приведенных ниже формул равносильны формуле:
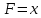 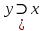 ˄z) ˄z)
а)  б) б)  в) в) 
Решение: состаим таблицы истиности:
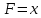 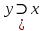 ˄z) ˄z)
x
|
y
|
z
|
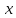 ˄z ˄z
|
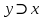 ˄z ˄z
|
F
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
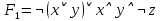
x
|
y
|
z
|

|
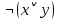
|
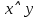
|

|
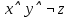
|

|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|

x
|
y
|
z
|

|
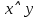
|
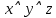
|

|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|

x
|
y
|
z
|

|
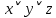
|

|

|

|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
Ответ: только a. |
|
|
 Скачать 152.88 Kb.
Скачать 152.88 Kb.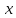 ˄z
˄z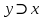 ˄z
˄z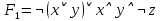

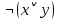
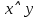

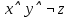



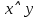
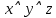



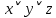




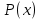 для каждого множества:
для каждого множества:
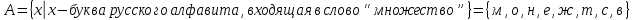
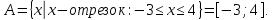
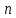 элементов, то множество-степень
элементов, то множество-степень 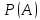 содержит
содержит 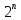 элементов.
элементов.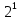 ) подмножества: ∅ и {a}.
) подмножества: ∅ и {a}.  ) подмножества: ∅, {a}, {b}, {b; a}.
) подмножества: ∅, {a}, {b}, {b; a}.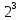 ) подмножества: ∅, {a}, {b}, {b; a}, {c}, {c; a},{c; b},{c; b; a}.
) подмножества: ∅, {a}, {b}, {b; a}, {c}, {c; a},{c; b},{c; b; a}. и если из предположения, что оно справедливо для произвольного
и если из предположения, что оно справедливо для произвольного  , можно доказать его справедливость для числа k + 1, то это свойство справедливо для всех натуральных чисел
, можно доказать его справедливость для числа k + 1, то это свойство справедливо для всех натуральных чисел 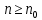 .
.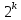 .
.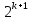 .
.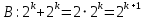 штук. Теорема доказана.
штук. Теорема доказана. , то, по определению отношения делимости x|x.
, то, по определению отношения делимости x|x. . Докажем от противного. Предположим, что x
. Докажем от противного. Предположим, что x y. По теореме: делитель y данного числа x не
y. По теореме: делитель y данного числа x не  и
и 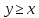 будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следовательно, наше предположение неверное и отношение делимости антисимметрично.
будут справедливы лишь тогда, когда а = b, что противоречит условию теоремы. Следовательно, наше предположение неверное и отношение делимости антисимметрично. . Контрпример 5 и 6
. Контрпример 5 и 6 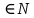 , но 5 не делит 6 и 6 не делит 5.
, но 5 не делит 6 и 6 не делит 5. :
: 
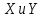 имеют равное количество элементов. Докажите, что это отношение является отношением эквивалентности и найдите классы эквивалентности.
имеют равное количество элементов. Докажите, что это отношение является отношением эквивалентности и найдите классы эквивалентности. .
.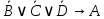 .
.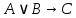 .
.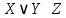 .
.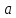 равен 0 или 1, то уравнение не имеет действительных решений.
равен 0 или 1, то уравнение не имеет действительных решений. .
.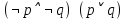 , если
, если 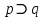 ложно?
ложно? формул (
формул (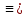 есть отношение эквивалентности, т.е. оно рефлексивно – для любой формулы А
есть отношение эквивалентности, т.е. оно рефлексивно – для любой формулы А  ; симметрично – для любых формул А и В, если А
; симметрично – для любых формул А и В, если А  , то В
, то В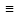 А; транзитивно – для любых формул А, В, С, если А
А; транзитивно – для любых формул А, В, С, если А  .
.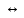 H является тавтологией: F
H является тавтологией: F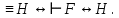
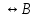 Тогда по тавтологии заключаем: формула B
Тогда по тавтологии заключаем: формула B 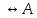 принимает всегда те же самые значения, что и формула
принимает всегда те же самые значения, что и формула  , т.е. только истинные значения. Следовательно, А
, т.е. только истинные значения. Следовательно, А  . Симметричность доказана.
. Симметричность доказана.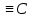 , т.е.
, т.е. 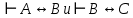 , то на основании определения конъюнкции заключаем, что:
, то на основании определения конъюнкции заключаем, что: 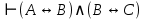 . Привлекая теперь тавтологию и правило заключения для получения тавтологий, получаем
. Привлекая теперь тавтологию и правило заключения для получения тавтологий, получаем 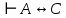 , или A
, или A  тогда и только тогда, когда эквиваленция формул А
тогда и только тогда, когда эквиваленция формул А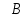 тождественно истинна.
тождественно истинна.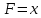
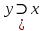 ˄z)
˄z) б)
б)