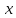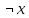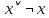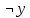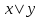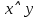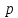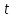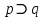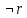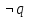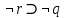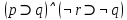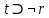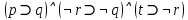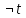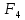КР по мат. логике Трипузова Карина Дмитриевна, МО 3.031.1.18. Контрольная работа по математической логике для студентов по мо озо 6 семестр (20202021 уч г.)
 Скачать 152.88 Kb. Скачать 152.88 Kb.
|
|
Задание 10. Выяснить, какие из перечисленных ниже формул являются тавтологиями: а) 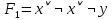 ; б) ; б) 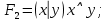 в) в) 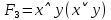 г) 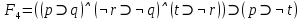 Решение: Изучая тавтологии, важно уяснить, что имеется простой и надежный алгоритм (общий метод), позволяющий для любой формулы логики высказываний дать ответ на вопрос, является она тавтологией логики высказываний или нет — этот алгоритм состоит в построении ее таблицы истинности. Составим таблицу истинности: a) 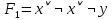
Последний столбец таблицы, состоящий из значений истинности данной формулы, содержит лишь единицы. Это означает, что данная формула — тавтология. б) 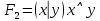
Последний столбец таблицы, состоящий из значений истинности данной формулы, содержит лишь единицы. Это означает, что данная формула — тавтология. в) 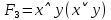
Последний столбец таблицы, состоящий из значений истинности данной формулы, содержит лишь единицы. Это означает, что данная формула — не является тавтологией. г) 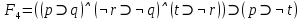 Первый способ.
Последний столбец таблицы, состоящий из значений истинности данной формулы, содержит лишь единицы. Это означает, что данная формула —тавтология. Второй способ. Предположим, что формула 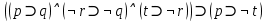 ложна при некоторых значениях высказывательных переменных P, Q, R и T.  Пришли к противоречию, следовательно, исходная формула — тавтология. Задание 11. Используя метод доказательства от противного, доказать, что а) если формулы 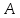 и и 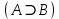 тождественно истинны, то формула тождественно истинны, то формула 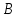 тождественно истинна; тождественно истинна;Решение: Предположим, что B=Л ложна. A=И и 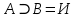 . Подставим B=Л A=И: . Подставим B=Л A=И: 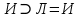 получили противоречие так как 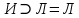 . . б) если формулы 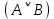 и и 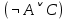 тождественно истинны, то формула тождественно истинны, то формула 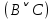 тождественно истинна; тождественно истинна;Решение: 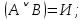 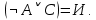 Предположим, что Предположим, что 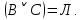 Это возможно при B=C=Л. Подставим в Это возможно при B=C=Л. Подставим в 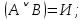 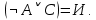 Получаем Получаем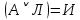 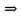 A=И A=И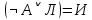 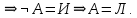 Получили, противоречие. в) если формулы 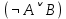 и и 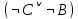 тождественно истинны, то формула тождественно истинны, то формула 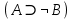 тождественно истинна. тождественно истинна.Решение: 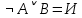 и и 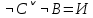 . Пусть . Пусть 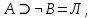 тогда A=И; тогда A=И; 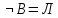 ; B=И. Подставим в ; B=И. Подставим в 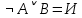 : :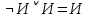 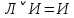 - верно. - верно.Подставим в 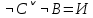 : :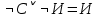 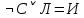 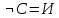 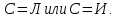 следовательно, исходное предположение о ложности неверно. |