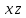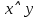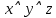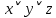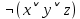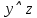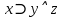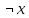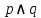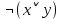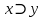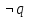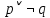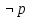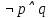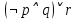КР по мат. логике Трипузова Карина Дмитриевна, МО 3.031.1.18. Контрольная работа по математической логике для студентов по мо озо 6 семестр (20202021 уч г.)
 Скачать 152.88 Kb. Скачать 152.88 Kb.
|
Задание 12. Используя метод доказательства от противного, докажите, что формула 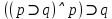 является тавтологией. является тавтологией.Решение: Предположим, что ((p⊃ q)&P) ⊃ q ложна при некоторых значениях пропозициональных переменных p и q. Представим наши рассуждения в виде таблицы. Каждая следующая строчка таблицы есть логическое следствие предыдущей строки.
Получили противоречие (q = И и q = Л одновременно), следовательно, исходное предположение о ложности ((p ⊃ q)&p) ⊃ q неверно, и получаем ⊧ ((p ⊃ q)&p) ⊃ q. Задание 13. Выяснить, какие из перечисленных ниже формул являются противоречиями: а) 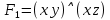 ; б) ; б) 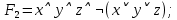 в) в) 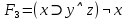 Решение: Строим таблицу истинности функций, реализующих формулы: а) 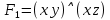
б) 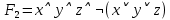
в) 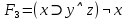
Анализ векторов истинности показывает, что все нули стоят только в векторе, соответствующем второму варианту формулы, следовательно, она является тождественно ложной. Ответ: б). Задание 14. Доказать выполнимость формулы 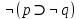 . .Доказательство: по определению импликации: 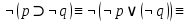 отрицание от дизъюнкция 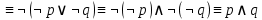 Получили 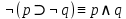 Составим таблицу истиности:
Для доказательства выполнимости формулы 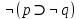 достаточно найти область определения т.е. формула принимает истинные значения. Формула выполнима при x=y=1. достаточно найти область определения т.е. формула принимает истинные значения. Формула выполнима при x=y=1. Пусть ¬(P ⊃ ¬P) = И. Тогда P ⊃ ¬P = Л, следовательно, P = И. Мы пришли к значению переменной P, при котором исходная формула истинна. Следовательно, формула ¬(P ⊃ ¬P) выполнима. Если бы пришли к противоречию, то это означало бы, что исходная формула не может быть истинной, следовательно, не является выполнимой. Задание 15. При каких значениях высказывательных переменных 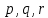 формула ( формула (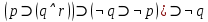 ложна? ложна?Решение: ( 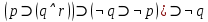 = Л ⇔ = Л ⇔( 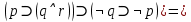 И, ¬q=Л. Таким образом, q=И и после подстановки И вместо q имеем (p ⊃ r) ⊃ (Л ⊃ ¬p) = И ⇔ (p⊃ r) ⊃ И = И ⇔ p rZ=И или p⊃r=Л. Следовательно, q=И и для любых значений p и r формула ложна. И, ¬q=Л. Таким образом, q=И и после подстановки И вместо q имеем (p ⊃ r) ⊃ (Л ⊃ ¬p) = И ⇔ (p⊃ r) ⊃ И = И ⇔ p rZ=И или p⊃r=Л. Следовательно, q=И и для любых значений p и r формула ложна.Задание 16. Докажите, что 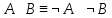 . .Решение. Имеем A B ≡ (A & B) ∨ (¬A & ¬B). С другой стороны, используя ту же равносильность, ¬A ¬B ≡ (¬A & ¬B) ∨ (¬¬A & ¬¬B) ≡ (¬A & ¬B) ∨ (A & B). Следовательно, AB ≡ ¬A¬B. Задание 17. Преобразовать к конъюнктивной нормальной форме (КНФ) и дизъюнктивной нормальной форме (ДНФ) формулу: 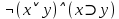 Решение:
CДНФ: 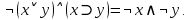 CКНФ: 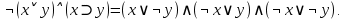 Задание 18. Привести к КНФ и ДНФ формулу: 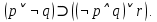 Будет ли она тождественно истинной, тождественно ложной? Будет ли она тождественно истинной, тождественно ложной?Решение:
CДНФ: 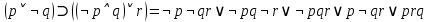 CКНФ: 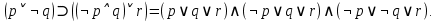 Будет ли она тождественно истинной, тождественно ложной. Ответ нет. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||