КР по мат. логике Трипузова Карина Дмитриевна, МО 3.031.1.18. Контрольная работа по математической логике для студентов по мо озо 6 семестр (20202021 уч г.)
 Скачать 152.88 Kb. Скачать 152.88 Kb.
|
|
Задание 21. Пусть даны предикаты на множестве натуральных чисел: 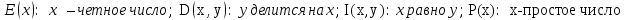 . Переведите на обычный язык следующие формулы и определите, истинны они или нет: . Переведите на обычный язык следующие формулы и определите, истинны они или нет:a) 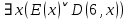 б) б) 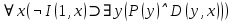 в) 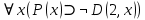 г) г) 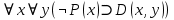 Решение: a) 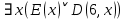 Существует натуральное число x которое четное и x делиться на 6. Утверждение верное. б) 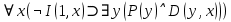 Для любого натурального числа x которое не равно 1 следует, что существует натуральное число y которое простое или x делиться на y. Утверждение верное. в) 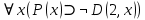 Для любого натурального числа x, где x –простое число следует, что x не делиться на 2. Утверждение верно. г) 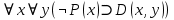 Для любых двух натуральных чисел x и y. Если x не простое число следует, что у делиться на x. Утверждение не верно. Задание 22. Пусть даны предикаты на множестве натуральных чисел: 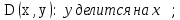 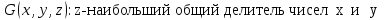 . .Запишите следующие утверждения на языке логики предикатов: а) если 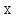 делится на делится на 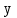 и и 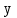 делится на z, то делится на z, то 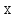 делится на z; делится на z;б) если d – наибольший общий делитель чисел 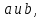 то то 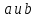 делятся на d и d делится на любой общий делитель чисел делятся на d и d делится на любой общий делитель чисел 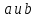 . .Решение: a) 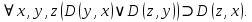 б) 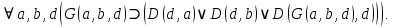 Задание 23. Пользуясь знаками арифметических действий 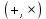 и отношений и отношений 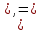 , запишите на языке логики предикатов следующие высказывания о действительных числах: , запишите на языке логики предикатов следующие высказывания о действительных числах:а) если произведение двух чисел равно нулю, то хотя бы один из сомножителей равен нулю; б) система уравнений 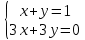 не имеет решения; не имеет решения;в) существует ровно одно положительное значение квадратного корня из положительного числа. Решение: а) 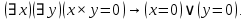 б) 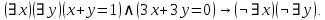 в) 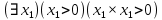 Задание 24. Пользуясь знаками арифметических действий 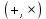 и отношений и отношений 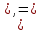 , запишите на языке логики предикатов каждое из следующих высказываний и определите, истинное оно или ложное: , запишите на языке логики предикатов каждое из следующих высказываний и определите, истинное оно или ложное:а) существует такое целое число 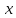 , что , что 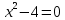 б) для любых действительных чисел 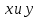 , если , если 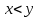 и и 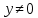 , то , то 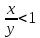 . .Решение: 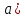 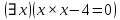 -верное -верноеб) 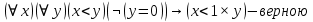 Задание 25. Используя только предикаты 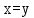 и и 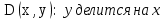 , запишите на языке логики предикатов следующие формулы от переменных, принимающих натуральные значения: , запишите на языке логики предикатов следующие формулы от переменных, принимающих натуральные значения:а) 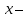 простое число; простое число;Решение: 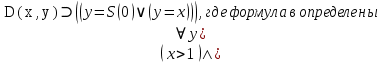 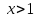 определено формулой определено формулой 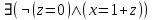 б) 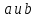 – взаимно простые числа. – взаимно простые числа.Решение: 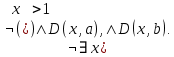 Задание 26. Выделите логическую форму приведенных ниже рассуждений (посылки и заключение) и определите те из них, которые построены по правилам: заключения (modus ponens), отрицания (modus tollens), силлогизма а) Все студенты нашей группы приняли участие в субботнике. Сидорова учится в нашей группе. Значит, она принимала участие в субботнике. Решение: Для решения вопроса о правильности умозаключения выявим его логическую форму. Введем обозначения: A(х) – « х – студент», В(х) – «x-принял участие в субботнике». Тогда первую посылку можно записать в виде: 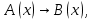 вторую вторую 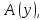 заключение заключение 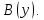 Наше умозаключение будет следующей логической формы: 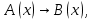 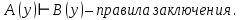 б) Все квадраты являются прямоугольниками. Во всех прямоугольниках диагонали равны. Следовательно, в любом квадрате диагонали равны. Решение: Для решения вопроса о правильности умозаключения выявим его логическую форму. Введем обозначения: A(х) – « х – квадрат», В(х) – «x-прямоугольник», C(x)- «диагонали равны». Тогда первую посылку можно записать в виде: 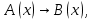 вторую вторую 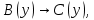 заключение заключение 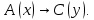 Наше умозаключение будет следующей логической формы: 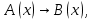 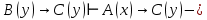 правило силлогизма. правило силлогизма.в) Если студент справился с контрольной работой, то он будет допущен к экзамену. Петрова не допущена к экзамену. Следовательно, она не справилась с контрольной работой. Решение: Введем обозначения: A(х) – « х – студент справился с контрольной работой », В(х) – «x-допущен к экзамену». Тогда первую посылку можно записать в виде: 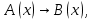 вторую вторую 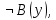 заключение заключение 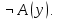 Данное умозаключение построено по правилу отрицания: 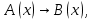 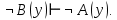 г) Если числитель дроби меньше знаменателя, то дробь правильная. Если дробь правильная, то она меньше единицы. Следовательно, если числитель дроби меньше знаменателя, то дробь меньше единицы. Решение: Введем обозначения: A(х) – « х – дробь правильная», В(х) – « x-числитель дроби меньше знаменателя», C(x)-«x меньше единицы». Тогда первую посылку можно записать в виде: 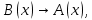 вторую вторую 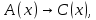 заключение заключение 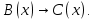 Данное умозаключение построено по правилу: 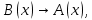 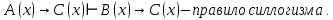 д) В любом ромбе диагонали взаимно перпендикулярны. В четырехугольнике АВСD диагонали не перпендикулярны. Следовательно, четырехугольник АВСD не является ромбом. Решение: Введем обозначения: A(х) – « х – ромб», C(x)-«в четырехугольнике х диагонали взаимно перпендикулярны». Тогда первую посылку можно записать в виде: 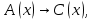 вторую вторую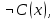 заключение заключение 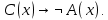 Данное умозаключение построено по правилу отрицания: 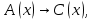 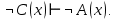 Задание 27. Выясните, правильны ли следующие рассуждения: а) Некоторые студенты педагогического университета являются учителями старших классов. Некоторые учителя старших классов старше 25 лет. Следовательно, некоторые студенты педагогического университета старше 25 лет. Решение: Для решения вопроса о правильности умозаключения выявим его логическую форму. Введем обозначения: A={студенты}; C={являются учителями}; B={ старше 25 лет }. Тогда первую посылку можно записать в виде: Некоторые студенты педагогического университета являются учителями старших классов: 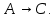 Вторая-Некоторые учителя старших классов старше 25 лет: 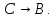 Некоторые студенты педагогического университета старше 25 лет: 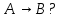 Таким образом, форма данного умозаключения такова: 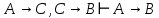 - правило силлогизма. Значит, данное умозаключение верно. б) Все глаголы отвечают на вопрос «что делать» или «что сделать». Слово «василек» не отвечает ни на один из этих вопросов. Следовательно, «василек» не является глаголом. Решение: Для решения вопроса о правильности умозаключения выявим его логическую форму. Введем обозначения: A(x)={x-глаголы}; C(x)={x-отвечают на вопрос «что делать» или «что сделать»}; y-слово «василек». Тогда первую посылку можно записать в виде: Все глаголы отвечают на вопрос «что делать» или «что сделать»: 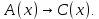 Вторая- Слово «василек» не отвечает ни на один из этих вопросов: 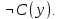 «василек» не является глаголом: 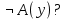 Таким образом, форма данного умозаключения такова: 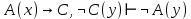 Данное умозаключение построено по правилу отрицания. Значит, данное умозаключение верно. Задание 28. Сформулируйте отрицания ниже приведенных высказываний: а) все студенты нашей группы были на лекции; б) некоторые студенты нашей группы не были на лекции; в) в каждой группе хотя бы один студент справился с контрольной работой. Решение: универсум: студенты; предикат A(x)= «x –студент были на лекции», а) все студенты нашей группы были на лекции ( 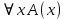 ) )Отрицание: 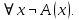 б) некоторые студенты нашей группы не были на лекции (( 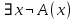 )) ))Отрицание: 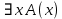 Задание 29. Дана теорема: «Если четырехугольник является ромбом, то его диагонали взаимно перпендикулярны». Сформулируйте теоремы, являющиеся обратной, противоположной и обратной противоположной данной. Верны ли эти теоремы? Решение: Введем обозначения: С(х) – «четырехугольник х – ромб», В(х) – «в четырехугольнике х диагонали взаимно перпендикулярны». Тогда первую посылку можно записать в виде: 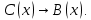 Обратная теорема: 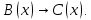 (неверно) (неверно)Обратной противоположной данной: 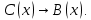 (верно) (верно)Аксиоматические теории и логический вывод Задание 30. Используя метод математической индукции, докажите свойство сократимости аксиоматического сложения натуральных чисел, а именно, «для любых натуральных чисел 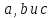 верно утверждение: если верно утверждение: если 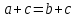 , то , то 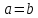 ». Докажите также обратное утверждение. ». Докажите также обратное утверждение.Доказательство: n=1: 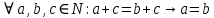 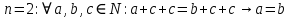 … n=k: 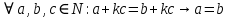 Проверим, что верно для n=k+1: 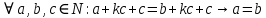 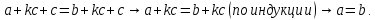 Обратное утверждение: 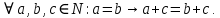 Доказательство: n=1: 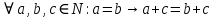 … n=k: 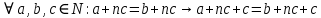 Проверим, что верно для n=k+1: 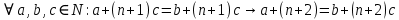 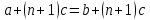 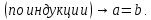 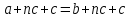 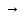 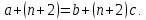 Задание 31. Используя метод от противного, докажите свойство сократимости аксиоматического умножения натуральных чисел, а именно, «для любых натуральных чисел 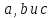 верно утверждение: если верно утверждение: если 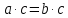 , то , то 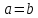 ». ». Доказательство: пусть 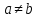 . Тогда . Тогда 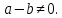 Получаем Получаем 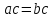 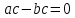 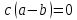 так как 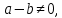 то с=0. Но c натуральное число. Получили противоречие. то с=0. Но c натуральное число. Получили противоречие.Задание 32. Используя доказательство контрпримером, докажите, что приведенные ниже рассуждения являются неправильными: а) Все числа, которые делятся на 4, делятся на 2. Число 127 не делится на 4. Следовательно, 127 не делится на 2. Решение: пример 2 не делиться на 4, но делиться 2. б) Все числа, которые делятся на 4, делятся на 2. Число 124 делится на 2. Следовательно, число 124 делится на 4. Решение: пример 2 делиться на 2, но не делиться 4. в) Все притоки Оби протекают по территории России. Иня протекает по территории России. Следовательно, она является притоком Оби. Решение: Река Волга протекает по Росии, но не является притоком Оби. Задание 33. Обосновать метод доказательства «разбором случаев»: для того чтобы доказать формулу 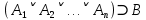 необходимо и достаточно доказать формулу необходимо и достаточно доказать формулу 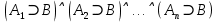 . .Доказательство. Пусть формула 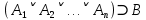 ложна (то, что мы начинаем доказательство, предполагая, что формула ложна, а не истинна, продиктовано тем обстоятельством, что при этом выборе доказательство короче), тогда формула B ложна, а ложна (то, что мы начинаем доказательство, предполагая, что формула ложна, а не истинна, продиктовано тем обстоятельством, что при этом выборе доказательство короче), тогда формула B ложна, а 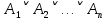 истинна. Следовательно, существует такое истинна. Следовательно, существует такое 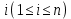 , что , что 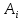 истинна и поэтому истинна и поэтому 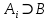 ложна. Отсюда следует, формула ложна. Отсюда следует, формула 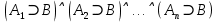 ложна. ложна.В обратную сторону. Пусть формула 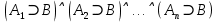 ложна. Следовательно, существует такое ложна. Следовательно, существует такое 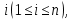 что Ai ⊃ B ложна. Отсюда получаем, что Ai истинна и B ложна и, следовательно, что Ai ⊃ B ложна. Отсюда получаем, что Ai истинна и B ложна и, следовательно, 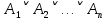 истинна и, наконец, истинна и, наконец, 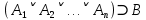 ложна. ложна.Логические задачи |
