математическое моделирование. ОСНОВЫ MATHCAD (1) (1). Введение Вычислительная мощность компьютера позволяет использовать его как средство автоматизации научной работы
 Скачать 1.1 Mb. Скачать 1.1 Mb.
|
Ввод текстаТекст, помещенный в рабочий лист, содержит комментарии и описание и предназначен для ознакомления, а не для использования в расчетах. Программа MathCad определяет назначение текущего блока автоматически при первом нажатии клавиши ПРОБЕЛ. Если введенный текст не может быть интерпретирован как формула, блок преобразуется в текстовый и последующие данные рассматриваются как текст. Создать текстовый блок без использования автоматических средств позволяет команда Insert Text Region (Вставка Текстовый блок). Стандартные и пользовательские функции Произвольные зависимости между входными и выходными параметрами задаются при помощи функции. Функции принимают набор параметров и возвращают значение, скалярное и векторное (матричное). В формулах можно использовать стандартные встроенные функции, а также функции, определенные пользователем. Чтобы использовать функцию в выражении, надо определить значение входных параметров в скобках после имени функции. Имена простейших математических функций можно ввести с панели инструментов Arithmetic (Счет). Информацию о других функциях можно почерпнуть в справочной системе. Вставить в выражение стандартную функцию можно при помощи команды Insert - Function (Вставка - Функция). В диалоговом окне Insert Function (Вставка функции) слева выбирается категория, к которой относится функция, а справа – конкретная функция. В нижней части окна выдается информация о выбранной функции. При вводе функции через это диалоговое окно автоматически добавляются скобки и заполнители для значений параметров. Пользовательские функции должны быть сначала определены. Определение задается при помощи оператора присваивания. В левой части указывается имя пользовательской функции и, в скобках, формальные параметры – переменные, от которых она зависит. Справа от знака присваивания эти переменные должны использоваться в выражении. При использовании пользовательской функции в последующих формулах ее имя вводят вручную. В диалоговом окне Insert Function (Вставка функции) оно не отображается. 2. Операции с векторами и матрицами Векторы и матрицы рассматриваются в программе MathCad как одномерные и двумерные массивы данных. Число строк и столбцов матрицы задается в диалоговом окне Insert Matrix (Вставка матрицы), которое открывают командой Insert Matrix (Вставка Матица). Вектор задается как матрица, имеющая один столбец После щелчка по кнопке ОК в формулу вставляется матрица, содержащая вместо элементов заполнители. Вместо каждого заполнителя надо вставить число, переменную или выражение. Для матриц определены следующие операции: сложение, умножение на число, перемножение и прочие. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы. Например, выражение М+3, где М- матрица, означает, Что к каждому элементу матрицы прибавляется число 3. Если требуется указать необходимость поэлементного применения операции к матрице, используют знак векторизации, для ввода которого служит кнопка Vectorize (Векторизация) на панели инструментов Matrix (Матрица). Например Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица). Пара индексов, определяющих элемент матрицы, разделяется запятой. Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки, например М<0>. Для своего ввода используется кнопка Matrix Column (Столбец) на панели инструментов Matrix (Матрица). Векторные и матричные операторы Для работы с векторами и матрицами система Mathcad содержит ряд операторов и функций. Вначале рассмотрим операторы, введя следующие обозначения для векторов V, для матриц M и для скалярных величин Z. Ниже представлены операторы для работы с векторами и матрицами. Оператор Ввод Описание
Следует отметить, что в некоторых операторах для ввода используется клавиша Ctrl, тогда как в более ранних версиях Mathcad использовалась клавиша Alt( в последней версии клавиша Alt используется для активизации строки меню). Все представленные выше операторы (кроме последнего) могут вызываться из палитры матричных операций. Работа с векторными и матричными функциямиСуществует также ряд встроенных векторных и матричных функций. Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц. Приведём список векторных функций, входящих в систему Mathcad: • length(V) – возвращает число элементов вектора. • last(V)- возвращает номер последнего элемента • max(V)- возвращает максимальный элемент по значению элемент вектора( или матрицы) • min(V)- возвращает минимальный по значению элемент вектора( или матрицы) • re(V)- возвращает вектор действительных частей вектора с комплексными элементами • Im(V)- возвращает вектор мнимых частей вектора с комплексными элементами Для работы с матрицами также существует ряд встроенных функций. Они перечислены ниже: • augment(M1, M2)- объединяет в одну две матрицы М1 и М2, имеющие одинаковое число строк ( объединение идет бок о бок) • identity(n)- создает единичную квадратную матрицу размером • stack(M1, M2)- объединяет две матрицы М1 и М2, имеющие одинаковое число столбцов, «сажая» М1 над М2 • submatrix(A, ir, jr, ic, jc)- возвращает подматрицу, состоящую из всех элементов, содержащихся в строках от ir до jr и столбцов c ic по jc ( ir ≤ jr и ic ≤ jc) • diag(V)- создает диагональную матрицу, элементы главной диагонали которой равны элементам вектора • matrix(m, n, f)- создает матрицу , в которой ( I , j)-й элемент равен а( I, j), где I=0, 1,…m и j=0,1,…n; f(I, j) некоторая функция. • Re(M)- возвращает матрицу действительных частей матрицы М с комплексными элементами. • Im(M)- возвращает матрицу мнимых частей матрицы М с комплексными элементами. Функции, возвращающие специальные характеристики матриц Следующие функции возвращают специальные характеристики матриц: • cols(M) - возвращает число столбцов матрицы М; • rows(M) - возвращает число строк матрицы М; • rank(M) - возвращает ранг матрицы М; • tr(M) - возвращает след (сумму диагональных элементов) квадратной матрицы М; • mean(M)- возвращает среднее значение элементов массива М; • median(M)- возвращает медиану элементов массива М; • cond1(M)- возвращает число обусловленности матрицы, вычисленное в норме L1; • cond2(M)- возвращает число обусловленности матрицы, вычисленное в норме L2; • conde(M)- возвращает число обусловленности матрицы, вычисленное в норме евклидового пространства; • condi((M)- возвращает число обусловленности матрицы, основанное на равномерной норме; • norm1(M)- возвращает норму L1 матрицы М; • norm2(M)- возвращает норму L2 матрицы М; • norme(M)- возвращает Евклидову норму матрицы М; • normi(M)- возвращает неопределённую норму матрицы М. Примеры применения векторных и матричных операторов. V:= V1:= V3:=V1·V2 V3=26 Умножение двух векторов V4:= V1 V:= U:= U  := ln(V) U= := ln(V) U=U1= 0.693 Выделение элемента вектора U Lenath(V) = 3 Вычисление встроенных функций вектора V Max(V)= 3 Mathcad делает работу с векторами и матрицами столь же простой, как и с обычными числами и переменными. Это, безусловно, способствует проникновению векторных и матричных методов математических вычислений в практику научно-технических и иных расчетов. Р ДЕЙСТВИЯ С МАТРИЦАМИ –1A:= B:= M:=identity(2) M= 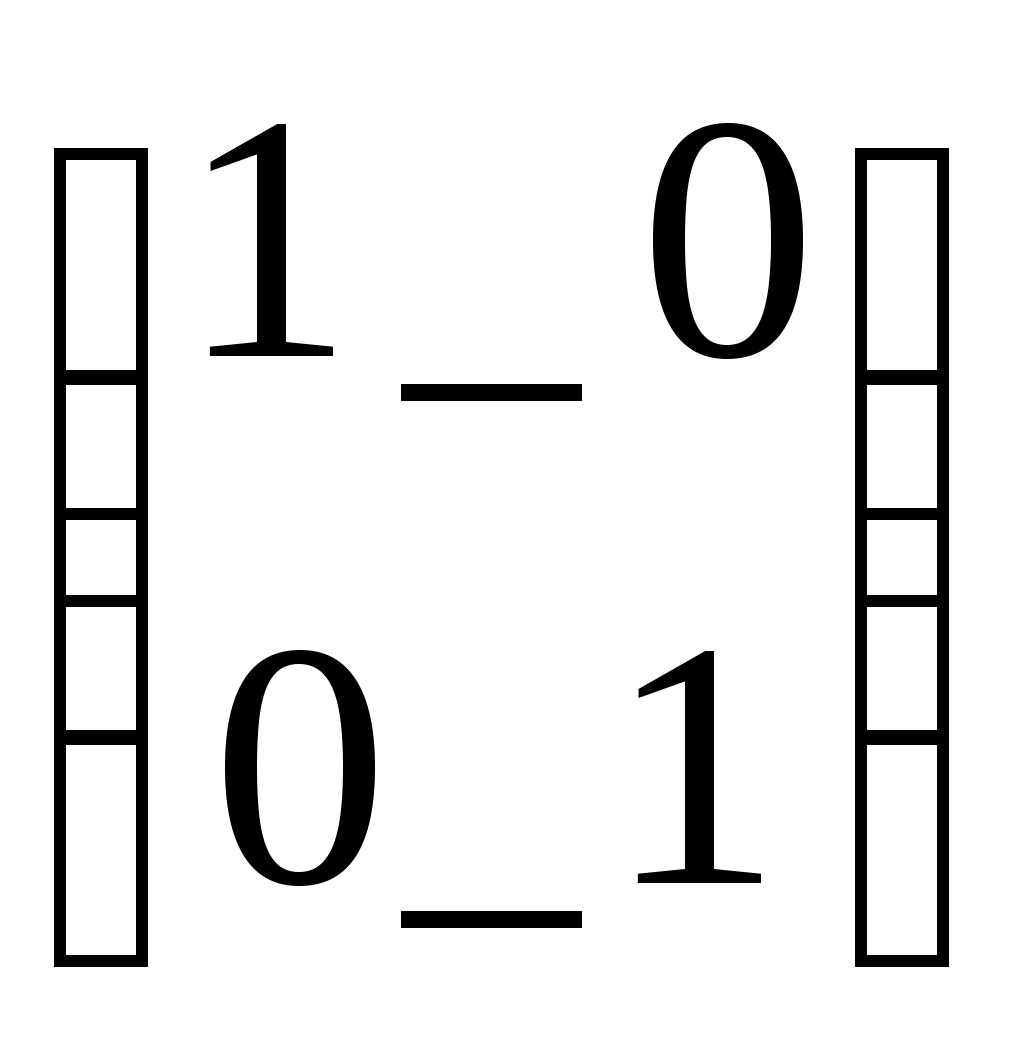 Создание единичной матрицы М Создание единичной матрицы МTr(M)=2 Вычисление следа матрицы A:= 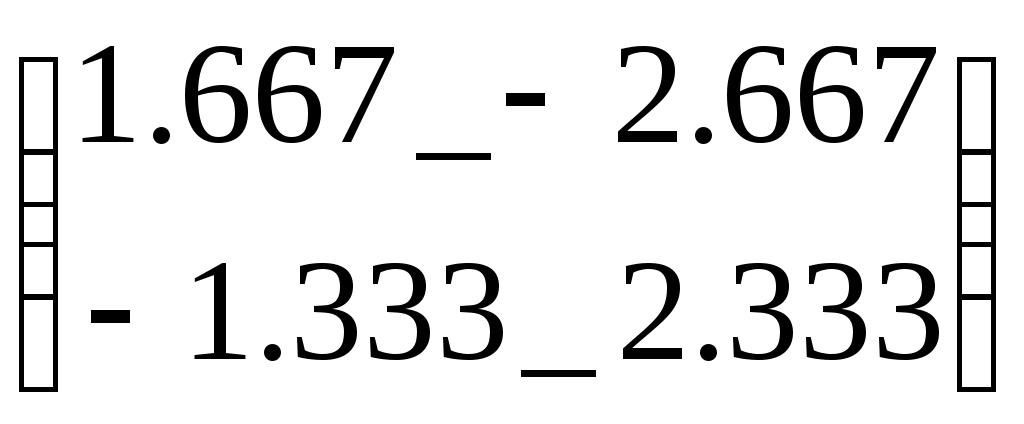 Задание и обращение матрицы А Задание и обращение матрицы АC:= A:= A:=  D:= D:=ДЕЙСТВИЯ С МАТРИЦАМИ –2А:= 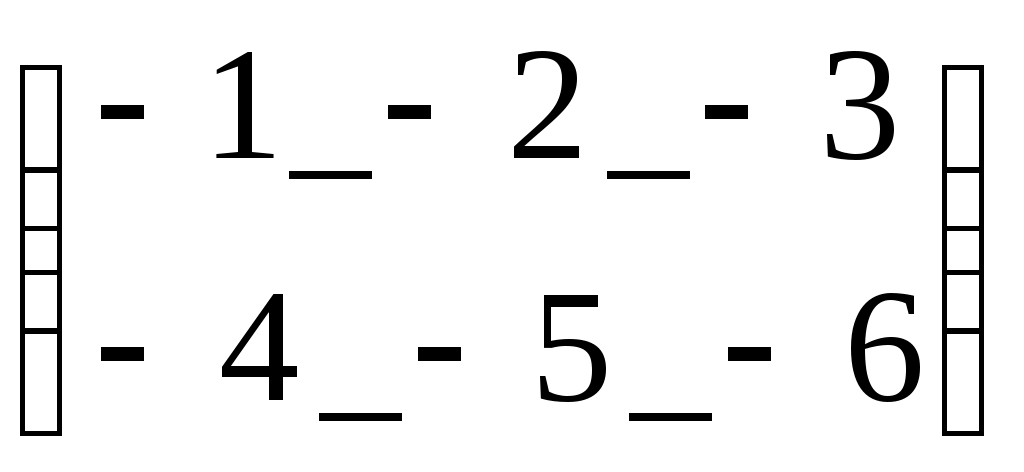 2·А= 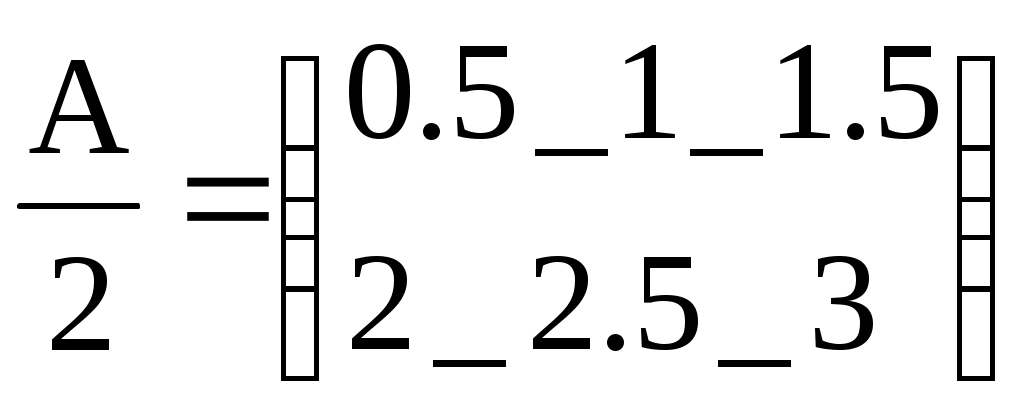 Задание матрицы А, смена знака у всех её Задание матрицы А, смена знака у всех её элементов, удвоение их и деление на два А:= W  :=exp(V) W= :=exp(V) W= Векторизация вектора W Векторизация вектора W I:= 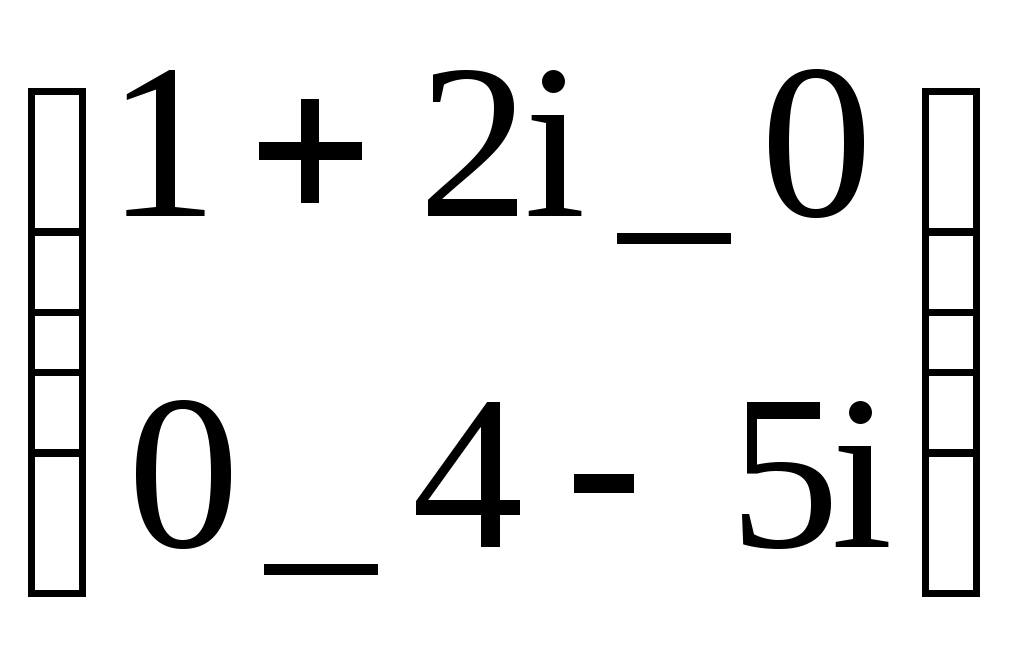 Задание матрицы А с комплексными элементами Задание матрицы А с комплексными элементамиM1:= identity(3) M1= 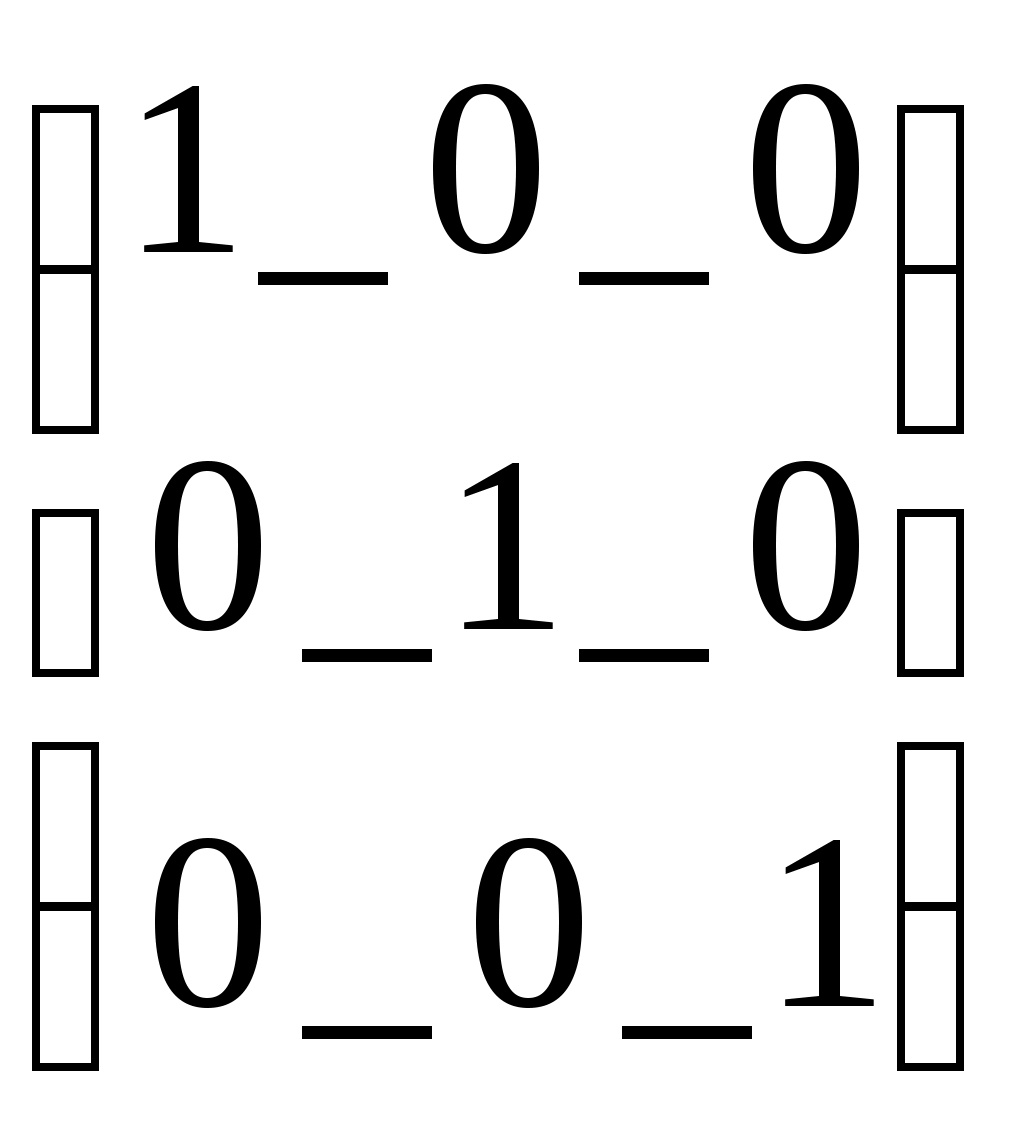 Задание и вывод единичной квадратной матрицы М1 Задание и вывод единичной квадратной матрицы М1 V:= М2:= 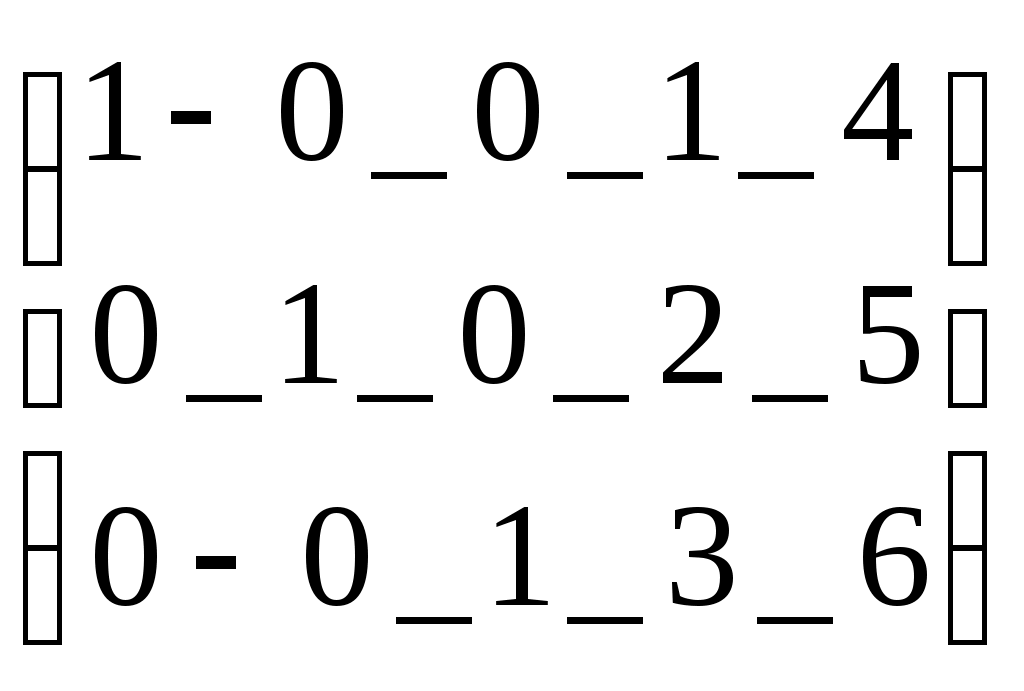 Задание матрицы М2 и подключение ее к матрице М1 Задание матрицы М2 и подключение ее к матрице М1Tr(M1)=3 Вычисление следа матрицы М1: суммы диагональных эдементов i:= Задание матрицы СМ с комплексными элементами CM:= 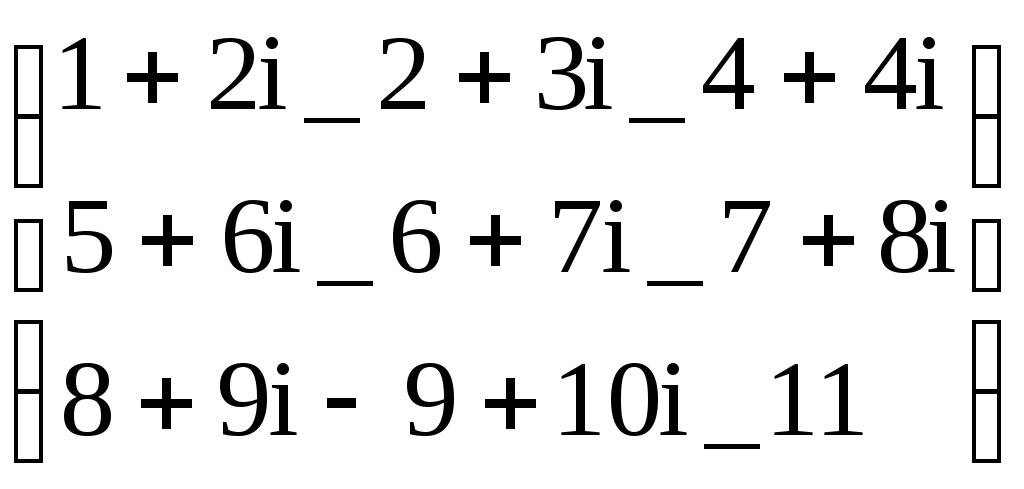 R:=Re(CM) R= 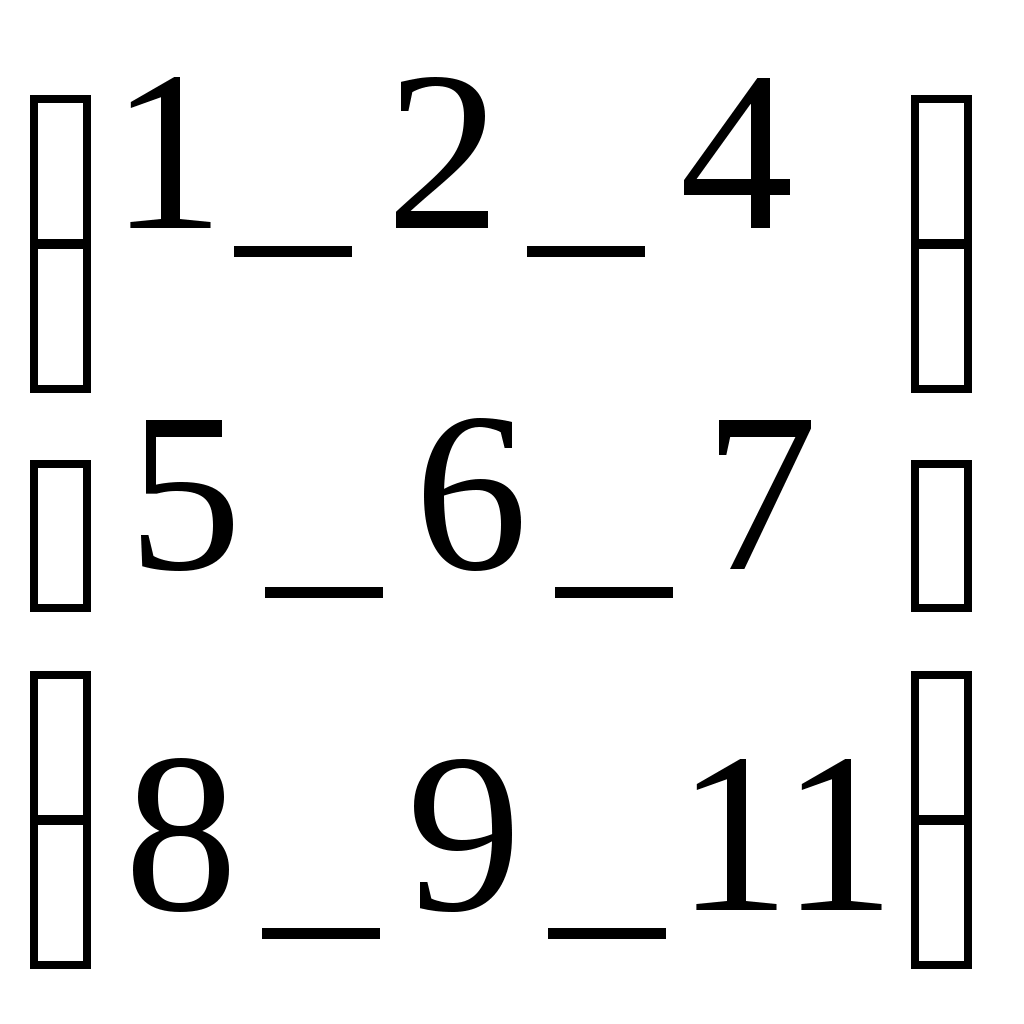 Выделение матрицы- действительной части матрицы СМ Выделение матрицы- действительной части матрицы СМ J:=lm(CM) J=  Выделение матрицы- мнимой части матрицы Выделение матрицы- мнимой части матрицы K:=1..3 L:=1..3 МС= 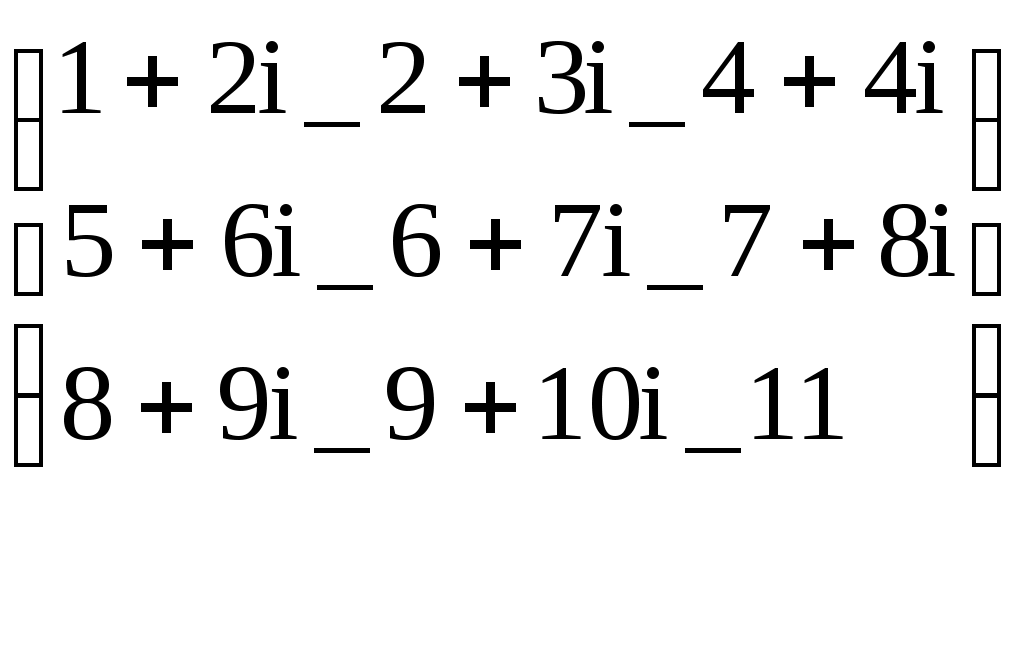 Вывод восстановленной матрицы ( МС=СМ) Вывод восстановленной матрицы ( МС=СМ)3. Ранжированные переменные До сих пор мы рассматривали переменные, которые имеют единственное значение. Однако в математике часто возникает необходимость в задании некоторого ряда значений – чаще всего упорядоченного. Например, для вычисления факториала N! = 12…(N-1)N нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Также упорядоченный ряд значений какой-то переменной (например абсциссы x) нужен для построения графика функции – Mathcad строит графики функций по точкам, соединяя их по отрезкам прямых. Для создания таких рядов в Mathcad используются так называемые ранжированные переменные. Иногда они заменяют управляющие структуры – циклы, однако полноценной такая замена всё же не является, в частности, потому что не предусмотрен выбор любого значения ранжированной переменной. В самом простом случае для создания ранжированной переменной используется выражение: Name := Nbegin . . Nend, где Name – имя переменной, Nbegin – её начальное значение, Nend – конечное значение, .. – символ, указывающий на изменение переменной в заданных пределах (он вводится знаком точки с запятой ;). Если Nbegin < Nend, то шаг изменения переменной будет равен +1, в противном случае –1. Для создания ранжированной переменной общего вида используется выражение: Name := Nbegin, (Nbegin + Step) . . Nend. Здесь Step – заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend, или отрицательным в противном случае). Примеры. 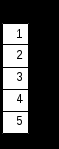 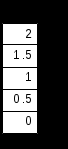 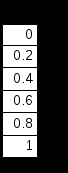  4. Построение графиков Чтобы построить двумерный график в координатных осях X-Y, надо дать команду Insert – Graph – X-Y Plot (Вставка – График – Декартовые координаты). В области размещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин. Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Обычно используют ранжированную переменную или вектор значений. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменения величины, но их можно задать и вручную. В одной графической области можно построить несколько графиков. Для этого надо у соответствующей оси перечислить несколько выражений через запятую. Разные кривые изображаются разным цветом, а для форматирования графика надо дважды щелкнуть на области графика. Для управления отображением построенных линий служит вкладка Traces (Линии) в открывшемся диалоговом окне. Текущий формат каждой линии приведен в списке, а под списком расположены элементы управления, позволяющие изменять формат. Поле Legend Label (Описание) задает описание линии, которое отображается только при сбросе флажка Hide Legend (Скрыть описание). Список Symbol (символ) позволяет выбрать маркеры для отдельных точек, список Line (тип линии) задает тип линии, список Color (Цвет) – цвет. Список Type (Тип) определяет способ связи отдельных точек, а список Width (Толщина) – толщину линии. Точно также можно построить и отформатировать график в полярных координатах. Для его построения надо дать команду Insert – Graph – Polar Plot (Вставка – График – Полярные координаты). 5. Решение уравнений и систем Для численного поиска корней уравнения в программе MathCad используется функция root. Она служит для решения уравнений вида Если уравнение имеет несколько корней (как в данном примере), то результат, выдаваемый функцией root, зависит от выбранного начального приближения. Если надо решить систему уравнений (неравенств), используют так называемый блок решения, который начинается с ключевого слова given (дано) и заканчивается вызовом find (найти). Между ними располагают логические выражения, задающие ограничения на значения искомых величин, иными словами, уравнения и неравенства. Всем переменным, используемым для обозначения неизвестных величин, должны быть заранее присвоены начальные значения. Чтобы записать уравнение, в котором утверждается, что левая и правая части равны, используется знак логического равенства – кнопка Boolean Equals (Логически равно) на панели инструментов Evaluation (Вычисление). Другие знаки логических условий также можно найти на этой панели. Заканчивается блок решения вызовом функции find, у которой в качестве аргументов должны быть перечисленные искомые величины. Эта функция возвращает вектор, содержащий вычисленные значения неизвестных. Например: 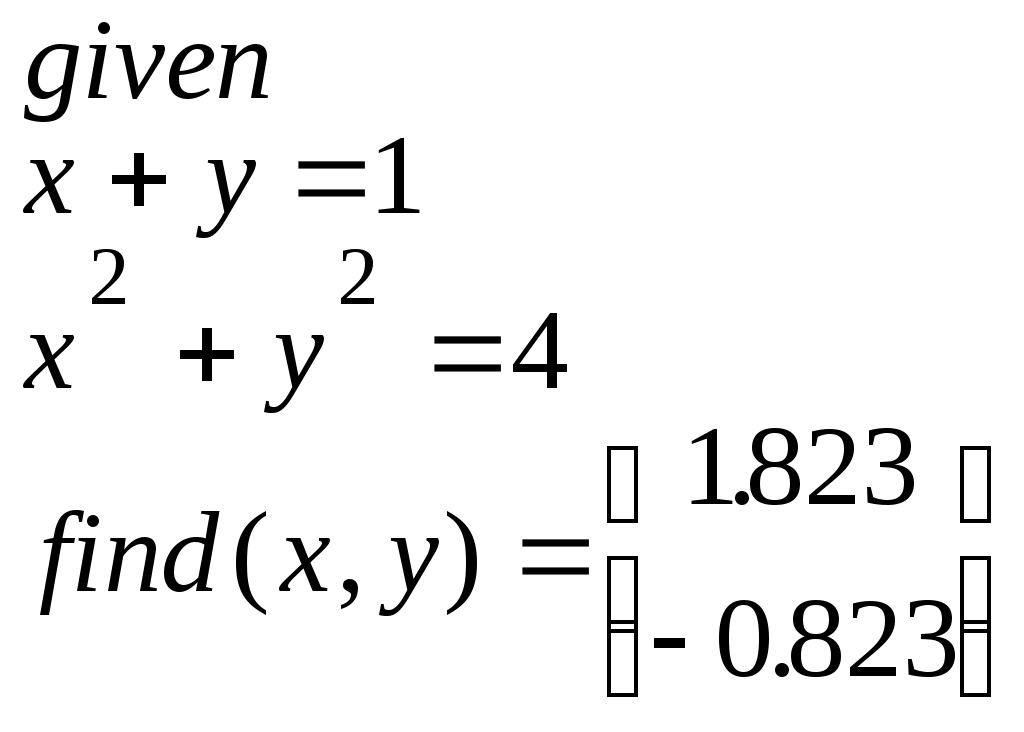 Для решения линейной системы уравнений Ax = b используется встроенная функция lsolve(A, b), где А – матрица системы, b – вектор правых частей. Функция возвращает вектор решений системы. |
