Взаимное расположение плоскостей в пространстве. Взаимное расположение плоскостей в пространстве. Угол между плоскостями
 Скачать 263.16 Kb. Скачать 263.16 Kb.
|
|
Взаимное расположение плоскостей в пространстве. Угол между плоскостями. Плоскость, прямая, точка — основные понятия геометрии. Нам трудно дать им четкие определения, однако интуитивно мы понимаем, что это такое. Плоскость имеет только два измерения. У нее нет глубины. Прямая имеет лишь одно измерение, а у точки вообще нет размеров — ни длины, ни ширины, ни высоты. Плоскость бесконечна. Поэтому в задачах мы рисуем только часть плоскости. Надо же как-то ее изобразить. 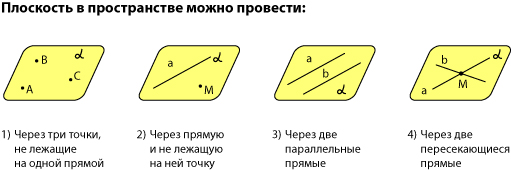 А как все это выглядит в пространстве? Очень просто. Лист плотной бумаги послужит «моделью» плоскости. Карандаши вполне могут изобразить прямые. Все аксиомы и теоремы стереометрии можно показать «на пальцах», то есть с помощью подручных материалов. Читаете — и сразу стройте такую «модель». Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко. Если две плоскости имеют общую точку, то они пересекаются по прямой. 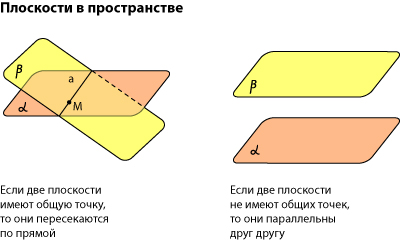 Мы не рассматриваем отдельно случай «плоскости совпадают». Раз совпадают — значит, это одна плоскость, а не две. Угол между плоскостями - определение. При изложении материала мы будем использовать определения и понятия, данные в статьях плоскость в пространстве и прямая в пространстве. Приведем рассуждения, которые позволят постепенно подойти к определению угла между двумя пересекающимися плоскостями. Пусть нам даны две пересекающиеся плоскости 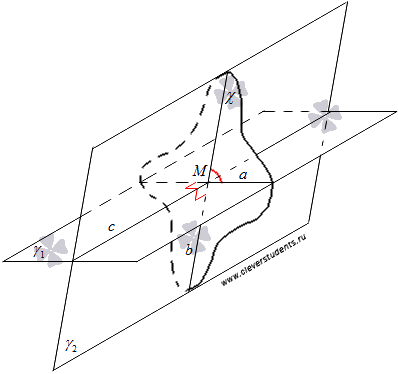 Легко показать, что угол между пересекающимися прямыми a и b не зависит от расположения точки М на прямой c, через которую проходит плоскость Построим плоскость Из способа построения плоскостей 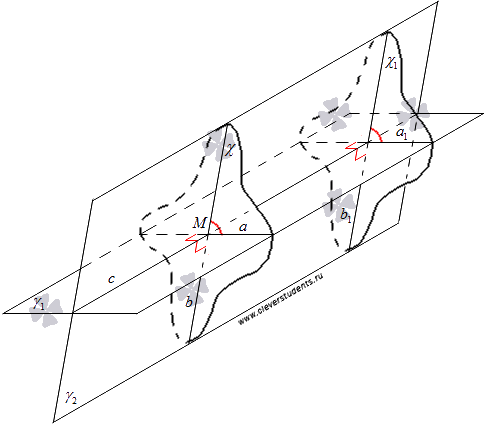 Этим доказано, что угол между пересекающимися прямыми a и b, лежащими в пересекающихся плоскостях Теперь можно озвучить определение угла между двумя пересекающимися плоскостями Определение. Угол между двумя пересекающимися по прямой c плоскостями 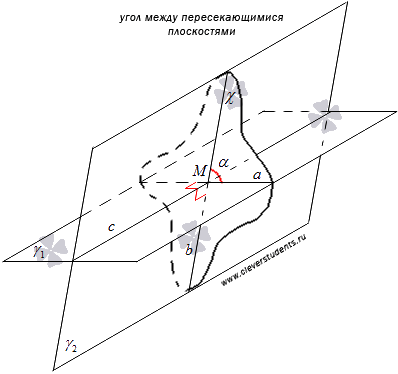 Определение угла между двумя плоскостями можно дать немного иначе. Если на прямой с, по которой пересекаются плоскости Так как угол между пересекающимися прямыми не превосходит К началу страницы Нахождение угла между двумя пересекающимися плоскостями. Обычно при нахождении угла между двумя пересекающимися плоскостями сначала приходится выполнять дополнительные построения, чтобы увидеть пересекающиеся прямые, угол между которыми равен искомому углу, и после этого связывать этот угол с исходными данными при помощи признаков равенства, признаков подобия, теоремы косинусов или определений синуса, косинуса и тангенса угла. В курсе геометрии средней школы встречаются подобные задачи. Для примера приведем решение задачи С2 из ЕГЭ по математике за 2012 год (условие намерено изменено, но это не влияет на принцип решения). В ней как раз нужно было найти угол между двумя пересекающимися плоскостями. Пример. Дан прямоугольный параллелепипед АВСDA1B1C1D1, в котором АВ=2, AD=3, АА1=7 и точка E делит сторону АА1 в отношении 4 к 3, считая от точки А. Найдите угол между плоскостями АВС и ВЕD1. Решение. Для начала сделаем чертеж. 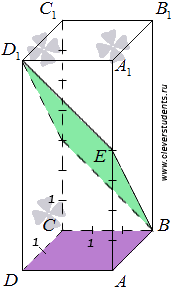 Выполним дополнительные построения, чтобы «увидеть» угол между плоскостями. Для начала определим прямую линию, по которой пересекаются плоскости АВС и BED1. Точка В – это одна из их общих точек. Найдем вторую общую точку этих плоскостей. Прямые DA и D1E лежат в одной плоскости АDD1, причем они не параллельны, а, значит, пересекаются. С другой стороны, прямая DA лежит в плоскости АВС, а прямая D1E – в плоскости BED1, следовательно, точка пересечения прямых DA и D1E будет общей точкой плоскостей АВС и BED1. Итак, продолжим прямые DA и D1E до их пересечения, обозначим точку их пересечения буквой F. Тогда BF – прямая, по которой пересекаются плоскости АВС и BED1. 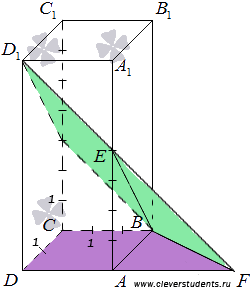 Осталось построить две прямые, лежащие в плоскостях АВС и BED1 соответственно, проходящие через одну точку на прямой BF и перпендикулярные прямой BF, - угол между этими прямыми по определению будет равен искомому углу между плоскостями АВС и BED1. Сделаем это. Точка А является проекцией точки Е на плоскость АВС. Проведем прямую, пересекающую под прямым углом прямую ВF в точке М. Тогда прямая АМ является проекцией прямой ЕМ на плоскость АВС, и по теореме о трех перпендикулярах 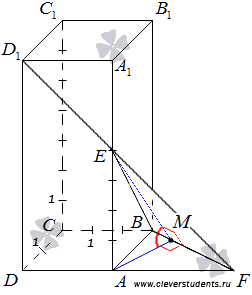 Таким образом, искомый угол между плоскостями АВС и BED1 равен Синус, косинус или тангенс этого угла (а значит и сам угол) мы можем определить из прямоугольного треугольника АЕМ, если будем знать длины двух его сторон. Из условия легко найти длину АЕ: так как точка Е делит сторону АА1 в отношении 4 к 3, считая от точки А, а длина стороны АА1 равна 7, то АЕ=4. Найдем еще длину АМ. Для этого рассмотрим прямоугольный треугольник АВF с прямым углом А, где АМ является высотой. По условию АВ=2. Длину стороны АF мы можем найти из подобия прямоугольных треугольников DD1F и AEF: 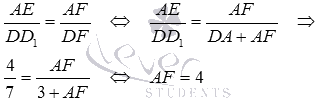 По теореме Пифагора из треугольника АВF находим 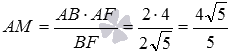 . .Таким образом, из прямоугольного треугольника АЕМ имеем 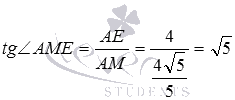 . .Тогда искомый угол между плоскостями АВС и BED1 равен 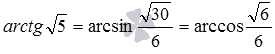 ). ).Ответ: 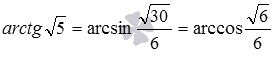 В некоторых случаях для нахождения угла между двумя пересекающимися плоскостями удобно задать прямоугольную систему координат Oxyz и воспользоваться методом координат. На нем и остановимся. Поставим задачу: найти угол между двумя пересекающимися плоскостями Будем считать, что в заданной прямоугольной системе координат Oxyz нам известны координаты нормальных векторов пересекающихся плоскостей Обозначим прямую, по которой пересекаются плоскости Отложим от точки М в плоскости 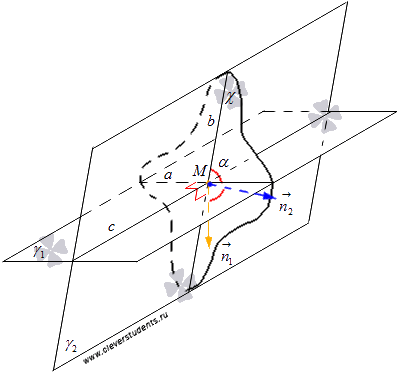 В статье нахождение угла между пересекающимися прямыми мы получили формулу, которая позволяет вычислять косинус угла между пересекающимися прямыми по координатам нормальных векторов. Таким образом, косинус угла между прямыми a и b, а, следовательно, и косинус угла между пересекающимися плоскостями 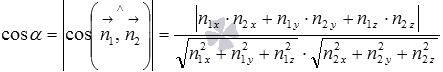 , где , где 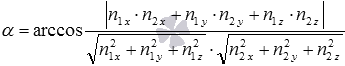 . .Решим предыдущий пример методом координат. Пример. Дан прямоугольный параллелепипед АВСDA1B1C1D1, в котором АВ=2, AD=3, АА1=7 и точка E делит сторону АА1 в отношении 4 к 3, считая от точки А. Найдите угол между плоскостями АВС и ВЕD1. Решение. Так как стороны прямоугольного параллелепипеда при одной вершине попарно перпендикулярны, то удобно ввести прямоугольную систему координат Oxyz так: начало совместить с вершиной С, а координатные оси Ox, Oy и Oz направить по сторонам CD, CB и CC1 соответственно. 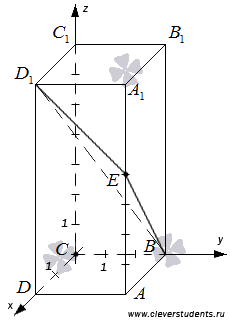 Угол между плоскостями АВС и BED1 может быть найден через координаты нормальных векторов этих плоскостей по формуле 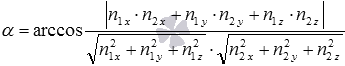 , где , где Так как плоскость АВС совпадает с координатной плоскостью Oxy, то ее нормальным вектором является координатный вектор В качестве нормального вектора плоскости BED1 можно принять векторное произведение векторов Очевидно, 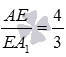 , то по координатам точек , то по координатам точек 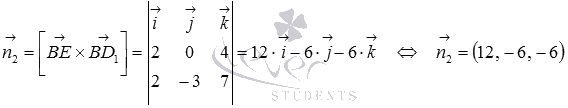 Осталось подставить найденные координаты в формулу для вычислений угла между плоскостями:  Как видите, метод координат дал такой же результат. Ответ:  В заключении разберем решение примера, в котором нужно найти угол между пересекающимися плоскостями по известным уравнениям этих плоскостей. Пример. Найдите синус угла, косинус угла и сам угол между двумя пересекающимися плоскостями, определенными в прямоугольной системе координат Oxyz уравнениями Решение. Когда мы изучали общее уравнение прямой вида Подставляем координаты нормальных векторов плоскостей в формулу для вычисления угла между двумя пересекающимися плоскостями: 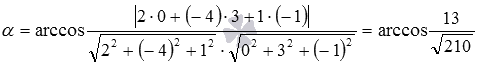 Тогда 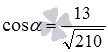 . Так как угол между двумя пересекающимися плоскостями не тупой, то с помощью основного тригонометрического тождества находим синус угла: . Так как угол между двумя пересекающимися плоскостями не тупой, то с помощью основного тригонометрического тождества находим синус угла: 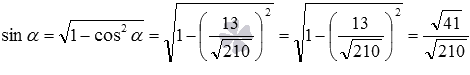 . .Ответ: 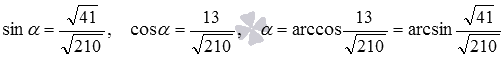 |
