|
И
15.01.2023
нформатика, 10 класс К.Ю. Поляков, Е.А. Еремин
Знакомство со средой Scilab
Свободно распространяемая среда Scilab (www.scilab.org) предназначена для выполнения научных и инженерных расчётов.
Где взять Scilab?
Инсталлятор Scilab для различных операционных систем можно скачать с официального сайта (www.scilab.org/download/). Там же можно скачать и её исходные коды.
Переносимую (не требующую установки) версию 5.5.2 для Windows можно загрузить по ссылке https://yadi.sk/d/_vBiEzaF-5vImQ. После распаковки архива нужно запускать файл WScilex.exe из подкаталога bin.
Можно использовать также облачную платформу cloud.scilab.in , в которой работает Scilab.
Два режима работы Scilab
Scilab – это интерпретатор команд, который может работать в двух режимах:
режим командной строки: команды вводятся в специальном окне, которое называется консолью, и сразу выполняются; в этом же окне система выводит ответ – результат вычислений или сообщение об ошибке:

В режиме командной строки удобно использовать Scilab как мощный калькулятор.
программный режим: пользователь составляет программу (скрипт), сохраняет её в файле и затем запускает файл на выполнение. Преимущество этого метода состоит в том, что в случае ошибки программу можно легко исправить, не набирая заново все команды. Scilab поддерживает простой язык программирования, который позволяет использовать переменные, циклы, условные вычисления, функции.
Чтобы открыть окно редактора скриптов, нужно щелкнуть по кнопке  в главном окне Scilab: в главном окне Scilab:

В редакторе нужно набрать последовательность команд, которые нужно выполнить, сохранить скрипт в виде файла и запустить, нажав клавишу F5. Результаты вычислений в таком режиме не выводятся автоматически в окно консоли; чтобы вывести значение переменной a нужно использовать команду
disp ( a )
Для выполнения практической работы достаточно использовать командный режим.
Уровень А.
Используя Scilab как калькулятор в режиме командной строки, вычислите значение выражения  . Для вычисления квадратного корня используйте встроенную функцию sqrt, число обозначается как %pi. Запишите ответ с точностью 0,001 (оставив 3 знака в дробной части числа). . Для вычисления квадратного корня используйте встроенную функцию sqrt, число обозначается как %pi. Запишите ответ с точностью 0,001 (оставив 3 знака в дробной части числа).
Ответ:
Функция dec2base переводит число в систему счисления с заданным основанием. Например, перевести число 100 в систему счисления с основанием 8 можно так:
--> dec2base(100,8)
Переведите число 567 в двоичную систему счисления:
Ответ:
Переведите число 259 в систему счисления с основанием 20:
Ответ:
Функция base2dec переводит число, записанное в системе счисления с заданным основанием, в десятичную систему счисления. Например, перевести число 1238 в десятичную систему счисления можно так:
--> base2dec("123", 8)
Обратите внимание, что первый аргумент – символьная строка в кавычках (это связано с тем, что в записи чисел в некоторых системах счисления могут быть латинские буквы).
Переведите число 11010100001012 в десятичную систему счисления:
Ответ:
Переведите число FEDCBA16 в десятичную систему счисления:
Ответ:
Уровень B.
Для построения графика функции y = f(x) нужно построить массив значений x, затем – массив соответствующих значений y, а затем вызвать встроенную функцию plot.
Для примера построим график функции y = 0,5xsin(2x) на отрезке [0; 10]. Сначала создаём массив (набор значений) независимой переменной x: от 0 до 10 с шагом 0,01:
--> x = 0:0.01:10
После ввода этой команды вы увидите на экране весь массив значений x. Чтобы не выводить его, в конце команды нужно поставить точку с запятой.
Затем строим массив значений y:
--> y = 0.5*x .* sin(2*x);
Обратите внимание, что в Scilab можно умножать число на массив (0.5*x), при этом получается новый массив того же размера, в котором все элементы исходного массива умножаются на указанное число. Также можно вызывать функции для массива (sin(2*x)), при этом также получается новый массив, в котором каждый элемент умножается на 2 и для результата вычисляется функция sin.
Дальше нужно перемножить элементы двух массивов – 0.5*x и sin(2*x). Эта операция (поэлементное умножение) обозначается двумя знаками «.*». Первый элемент первого массива умножается на первый элемент второго и т.д.
Теперь строим график:
--> plot(x, y)
Наконец, добавим на график ось OX как отрезок, соединяющий точки (0, 0) и (10, 0)
--> plot([0 10], [0 0], 'black')
Последний аргумент функции – это цвет линии (англ. black – чёрный).
Выполните эти команды в Scilab и вставьте в отчёт полученный график функции
y = 0,5xsin(2x) :
График:
Используя средства Scilab, постройте график функции 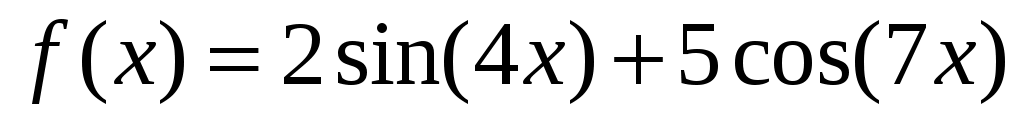 на отрезке [0; 3] и вставьте его в отчёт. на отрезке [0; 3] и вставьте его в отчёт.
График:
Определите, сколько решений имеет уравнение 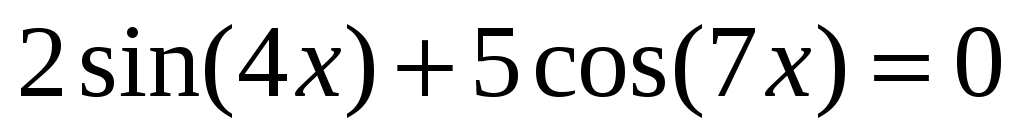 на отрезке [0,5; 1,8]? на отрезке [0,5; 1,8]?
Ответ:
Уровень С.
Среда Scilab умеет выполнять операции с полиномами (многочленами). Сначала создадим базовую переменную, например, x:
--> x = poly(0, "x")
Первый аргумент функции poly – массив корней нового полинома, второй – имя переменной. Таким обрназом, приведённый выше вызов создаёт полином с единственным корнем 0 и именем переменной x. Теперь можно строить полиномы от этой переменной:
--> p1 = x - 5
--> p2 = x^2 - 3*x + 2
выполнять с ними операции (складывать, вычитать, умножать):
--> p = p1*p2 + 4
находить корни полинома (значения x, при которых он равен 0) с помощью функции roots:
--> r = roots(p)
Выполните приведённые выше команды и запишите полином p, который у вас получился. Обратите внимание, что Scilab выводит полином в порядке возрастания степеней (от свободного члена к старшей степени x), а в математике принят обратный порядок записи.
Запишите коэффициенты полинома вместо многоточий:
p(x) = … x3 + … x2 + … x + …
Вычислите корни этого полинома:
Найдите корни полинома 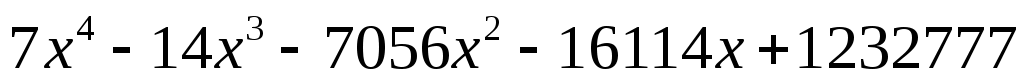 : :
Ответ:
В среде Scilab можно легко решать системы линейных уравнений. Покажем, как решить систему
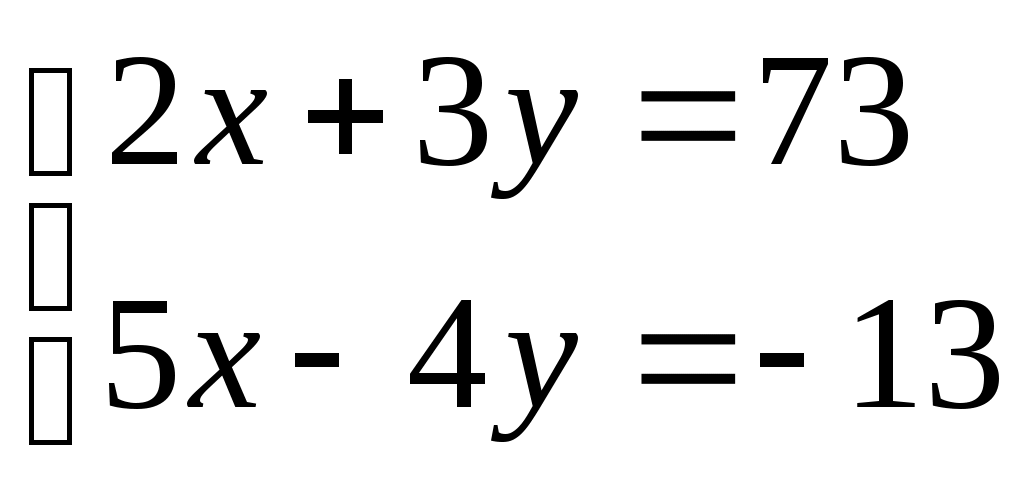
Из коэффициентов левых частей этих уравнений можно составить матрицу (прямоугольную таблицу) 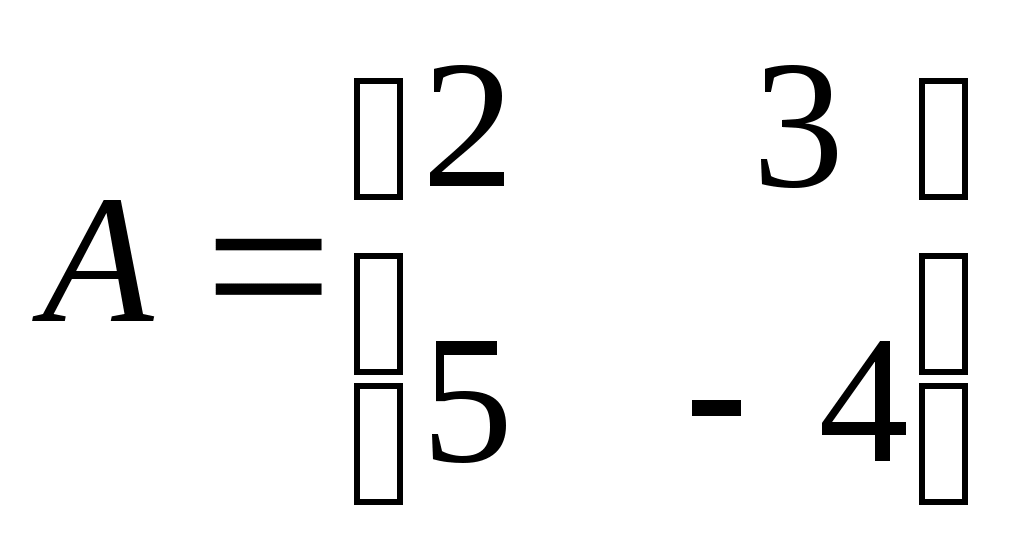 , а правые части образуют массив (вектор) , а правые части образуют массив (вектор)  . Тогда исходную систему уравнений можно записать в матричном виде: . Тогда исходную систему уравнений можно записать в матричном виде:
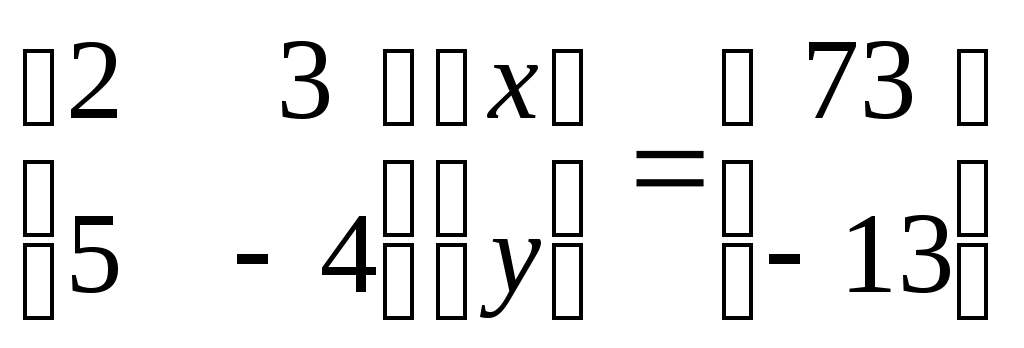
Например, для того, чтобы получить первое уравнение системы, первую строку матрицы A нужно поэлементно умножить на вектор (столбец) неизвестных.
В среде Scilab матрицы (а массив B – тоже матрица, только из одного столбца) записываются по строкам, строки отделяются друг от друга точкой с запятой:
--> A = [2 3;5 -4]
--> B = [73; -13]
Теперь столбец с неизвестными переменными x и y получается с помощью специального матричного деления:
--> A \ B
Выполните приведённые выше команды и найдите значения переменных x и y.
Ответ:
x = …, y = …
Уровень D.
Решите систему уравнений
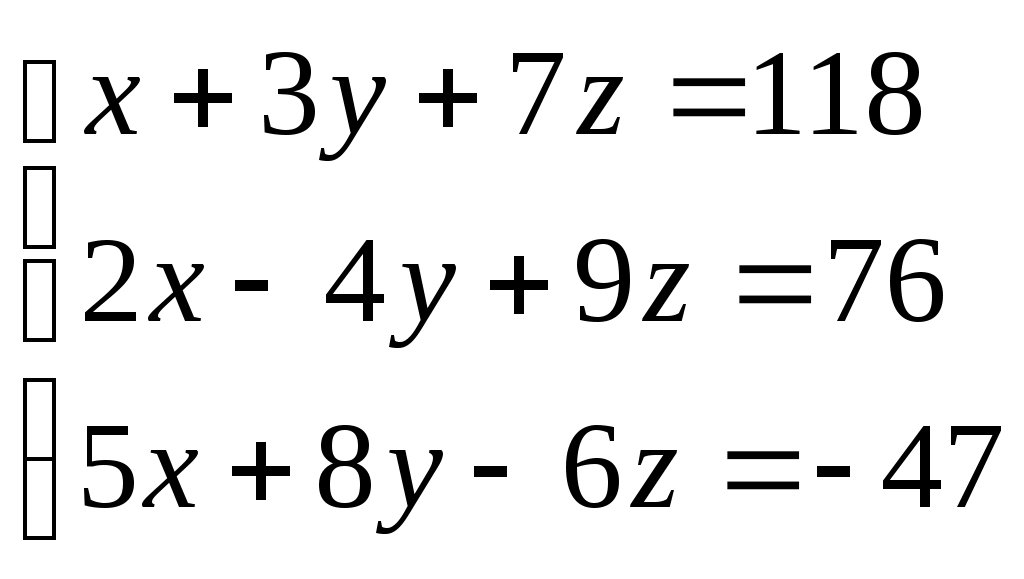
Ответ:
x = …, y = …, z = …
Среда Scilab позволяет решать задачи оптимизации, то есть находить значения переменной (или нескольких переменных), при которых функция достигает минимума (или максимума). Самая простая функция из этой группы – fminsearch – ищет минимум заданной функции без дополнительных ограничений. Функция, минимум которой мы ищем, должна быть определена с помощью специальной команды deff:
--> deff("y=f(x)", ["y = x^2 + 3*x + 5;"])
Эта строчка определяет функцию  , которая в среде Scilab получает имя f. , которая в среде Scilab получает имя f.
В скрипте та же самая функция может быть определена иначе:
function y = f(x)
y = x^2 + 3*x + 5;
endfunction
Теперь осталось выполнить оптимизацию, вызвав встроенную функцию fminsearch:
--> [xmin, ymin] = fminsearch(f, 1)
Слева от знака равенства в квадратных скобках записаны имена двух переменных – это означает, что функция вернёт два значения – координаты точки минимума (xmin, ymin).
Первый аргумент функции fminsearch – это имя функции, минимум которой нужно найти. Поиск начинается со значения x = 1 (это второй аргумент). Если минимумов несколько, то будет найдён тот, в который «скатится шарик», установленный на линии в начальной точке (см. рисунок ниже).

Такой минимум называется «локальным». Чтобы найти «самый глубокий» или «глобальный» минимум, нужно выбрать правильное начальное приближение.
Найдите координаты точки минимума функции  : :
Ответ:
xmin = …, ymin = …
Найдите координаты точки глобального минимума функции 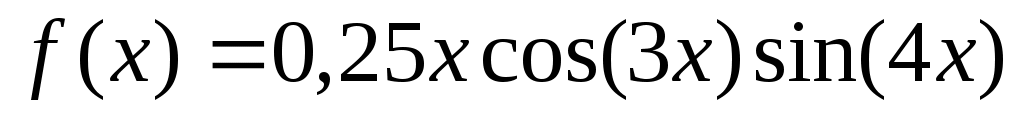 на отрезке [0; 10]: на отрезке [0; 10]:
График функции:
Начальное приближение:
Ответ (с точностью до трёх знаков после запятой):
xmin = …, ymin = …
Онлайн-сервисы для разработки презентаций
Работа в группах по 3-4 человека. Используя онлайн-сервисы для разработки презентаций, например,
презентации Google
prezi.com
www.canva.com
разработайте презентацию на выбранную тему. Сделайте краткое сообщение перед классом с показом презентации. Обсудите достоинства и недостатки онлайн-сервисов для создания презентаций.
http://kpolyakov.spb.ru
|
 Скачать 185 Kb.
Скачать 185 Kb.