лекция 9. Xiii. Постоянный электрический ток. 92. Электрический ток. Сила тока. Плотность тока
 Скачать 5.37 Mb.
|
Глава XIV. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ.§102. Электрический ток в металлах. Доказательство электронной природы тока в металлах. Электрический ток в металлах – это упорядоченное движение электронов под действием электрического поля. При протекании тока по металлическому проводнику не происходит переноса вещества, следовательно, ионы металла не принимают участия в переносе электрического заряда.
Свободные электроны способны блуждать по всему объему кристалла. Доказательство электронной природы тока в металлах было получено в опытах Л. И. Мандельштама и Н. Д. Папалекси (1913 г.), а так же в опытах Р. Толмена и Б. Стюарта(1916 г) с инерцией электронов. (рис.14.2)
Сторонняя сила, отнесенная к единице заряда, по определению является напряженностью Eст поля сторонних сил: На основании результатов опытов Толмена и Стюарта было установлено, что носители свободного заряда в металлах имеют отрицательный знак, а отношение заряда носителя к его массе близко к удельному заряду электрона, полученному из других опытов: модуль заряда электрона (элементарный заряд) равен  , а его удельный заряд  .Высокая электропроводность металлов объясняется высокой концентрацией свободных электронов, равной по порядку величины числу атомов в единице объема. Классическая электронная теория проводимости металлов (теория П. Друде и Х. Лоренца). Согласно этой теории, электроны в металлах ведут себя как электронный газ, во многом похожий на идеальный газ. Из-за взаимодействия с ионами электроны могут покинуть металл, лишь преодолев так называемый потенциальный барьер. Высота этого барьера называется работой выхода. При обычных (комнатных) температурах у электронов не хватает энергии для преодоления потенциального барьера.
Согласно теории Друде–Лоренца, электроны обладают такой же средней энергией теплового движения, как и молекулы одноатомного идеального газа. Это позволяет оценить среднюю скорость  теплового движения электронов по формулам молекулярно-кинетической теории. При комнатной температуре она оказывается примерно равной 10 5 м/с.При наложении внешнего электрического поля в металлическом проводнике кроме теплового движения электронов возникает их упорядоченное движение (дрейф), то есть электрический ток. (рис.14.4) Среднюю скорость  дрейфа можно оценить следующим образом. За интервал времени Δt через поперечное сечение S проводника пройдут все электроны, находившиеся в объеме  . Число таких электронов равно  где n – средняя концентрация свободных электронов, примерно равная числу атомов в единице объема металлического проводника.
Концентрация n атомов в металлах находится в пределах 1028–1029 м –3. Оценка по этой формуле для металлического проводника сечением 1 мм2, по которому течет ток 10 А, дает для средней скорости упорядоченного движения электронов значение в пределах 0,6–6 мм/c. Таким образом, средняя скорость упорядоченного движения электронов в металлических проводниках на много порядков меньше средней скорости их теплового движения ( << ). Малая скорость дрейфа не противоречит опытному факту, что ток во всей цепи постоянного тока устанавливается практически мгновенно. Замыкание цепи вызывает распространение электрического поля со скоростью c = 3·108 м/с. Через время порядка l / с (l – длина цепи) вдоль цепи устанавливается стационарное распределение электрического поля и в ней начинается упорядоченное перемещение (движение) электронов.В классической электронной теории металлов предполагается, что движение электронов подчиняется законам механики Ньютона. В этой теории пренебрегают взаимодействием электронов между собой, а их взаимодействие с положительными ионами сводят только к соударениям. Предполагается также, что при каждом соударении электрон передает решетке всю накопленную в электрическом поле энергию и поэтому после соударения он начинает движение с нулевой дрейфовой скоростью. Несмотря на то, что все эти допущения являются весьма приближенными, классическая электронная теория качественно объясняет законы электрического тока в металлических проводниках. Закон Ома. В промежутке между соударениями на электрон действует сила, равная по модулю eE, в результате чего он приобретает ускорение  . Поэтому к концу свободного пробега дрейфовая скорость электрона равна  ,где  – время свободного пробега, которое предполагается одинаковым для всех электронов. Среднее значение скорости дрейфа равно половине максимального значения: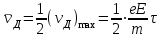 .Для проводника длиной l и сечением S, с концентрацией электронов n, ток в проводнике может быть записан в виде:  ,где U = El – напряжение на концах проводника. Полученная формула выражает закон Ома для металлического проводника. Электрическое сопротивление проводника равно:  ,а удельное сопротивление ρ и удельная проводимость 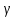 выражаются соотношениями:  ;  .Закон Джоуля-Ленца. К концу свободного пробега электроны приобретают под действием поля кинетическую энергию  .Согласно сделанным предположениям, вся эта энергия передается решетке при соударении и переходит в тепло. За время Δt каждый электрон испытывает Δt / τ соударений. В проводнике сечением S и длины l имеется nSl электронов. Отсюда следует, что выделяемое в проводнике за время Δt тепло равно:  .Это соотношение выражает закон Джоуля-Ленца. Таким образом, классическая электронная теория объясняет существование электрического сопротивления металлов, законы Ома и Джоуля-Ленца. Однако, в ряде вопросов классическая электронная теория приводит к выводам, находящимся в противоречии с опытом. Классическая электронная теория не может, например, объяснить температурную зависимость удельного сопротивления металлов. Теория дает ρ  в то время как из эксперимента получается зависимость ρ T. Объяснение механизма этого явления было дано только через 60 лет после его открытия на основе квантово – механических представлений. |
Рис.14.1
, которая играет роль сторонней силы, то есть силы неэлек-трического происхождения.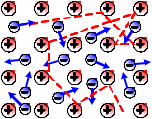
.
.