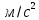ргз. Явление, изучаемое в расчетнографической работе
 Скачать 40.04 Kb. Скачать 40.04 Kb.
|
|
Явление, изучаемое в расчетно-графической работе – прямолинейное движение материальной точки. Определение основных величин, процессов, явлений, объектов: Тело отсчета – произвольно выбранное тело, относительно которого определяется положение движущейся материальной точки/тела Координата – это совокупность чисел или независимых переменных, которые определяют положение точки в пространстве. Система отсчета – это совокупность тела отсчета, системы координат и системы отсчета времени, связанных с этим телом, по отношению к которому изучается движение (или равновесие) каких-либо других материальных точек или тел. Траектория – линия, которую описывает материальная точка при своем движении. Если точка, двигаясь по траектории переместилась из точки один в точку два, то это расстояние называется длиной пройденного пути или просто пройденной частицей пути. Материальная точка – это тело, размерами, которых можно пренебречь по сравнению с расстоянием до других тел. Скорость – векторная величина, характеризующая быстроту движения и его направление в данный момент времени. Перемещение – вектор, проведенный из начального положения частицы в конечное. Средняя скорость – равна отношению перемещения тела к промежутку времени, за который это перемещение произошло. Является векторной величиной. 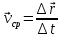 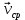 – средняя скорость; [ – средняя скорость; [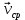 ]=м/с. ]=м/с.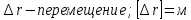 Средняя путевая скорость – это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден. Является скалярной величиной. 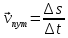 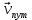 – средняя путевая скорость; [ – средняя путевая скорость; [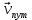 ]=м/с. ]=м/с.Ускорение – производная скорости по времени 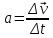 . .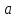 – ускорение; [ – ускорение; [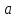 ]=м/с2. ]=м/с2.Средняя скорость 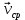 за интервал времени за интервал времени 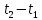 определяется: определяется: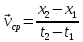 Средняя путевая скорость за время от 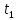 до до 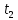 : :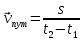 Ускорение равно значению первой производной от скорости по времени: 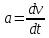 Вычисления: 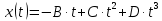 , где, , где, 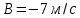 ; ; 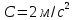 ; ; 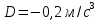 . .Дано: 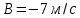 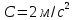 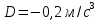 . .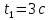 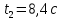 Решение: 1)Средняя путевая скорость 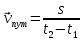 , где s-полный путь , где s-полный путьПо определению скорость точки равна первой производной по времени от закона изменения координаты: 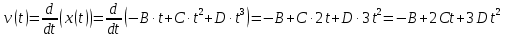 Определяем меняла ли направление скорость материальной точки в заданном промежутке времени от 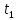 до до 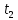 . по условию. Для этого приравняем полученную выше зависимость скорости точки от времени к нулю. . по условию. Для этого приравняем полученную выше зависимость скорости точки от времени к нулю.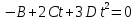 Т.к уравнение квадратное, то решать его будем через дискриминат, для этого его нужно посчитать: Дис= 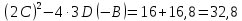 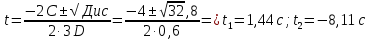 Получим две временные отметки, обе из которых не принадлежат временному промежутку, обозначенному в условии, а значит средняя путевая скорость и средняя скорость равны; 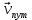 = =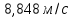 2) Средняя скорость: 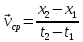 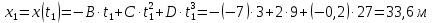 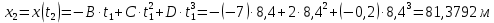 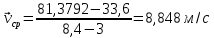 3) Среднее ускорение: 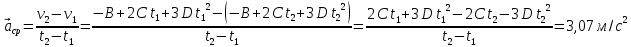 Графические вычисления: График зависимости координаты от времени 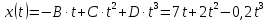
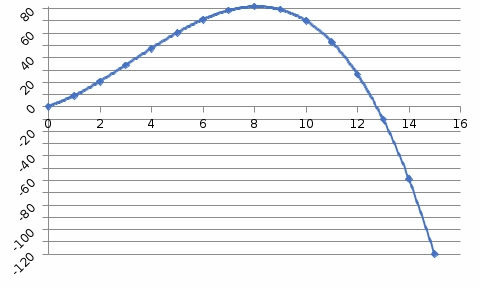 Рис.1 Зависимость х(t) График зависимости ускорения от времени: 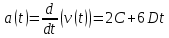 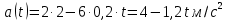
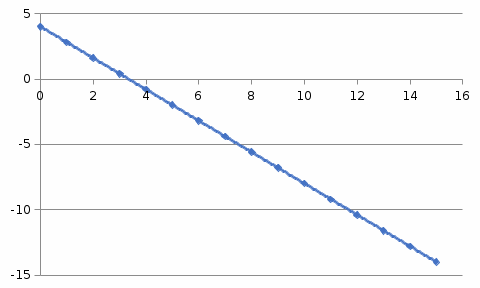 Рис.2. Зависимость a(t) Анализ полученных результатов: В результате выполнения РГР были рассчитаны для промежутка времени от 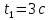 до до 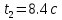 ; средняя скорость в период времени t1 и t2 ; средняя скорость в период времени t1 и t2 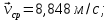 средняя путевая скорость средняя путевая скорость 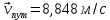 ; среднее значение ускорения ; среднее значение ускорения 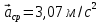 . .Построены графики зависимости координаты 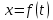 (Рис. 1) и ускорения (Рис. 1) и ускорения 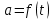 (Рис. 2) от времени в промежутке от 0 до 15 с. Координата положения тела менялась с течением времени, ускорение менялось согласно уравнению зависимости (Рис. 2) от времени в промежутке от 0 до 15 с. Координата положения тела менялась с течением времени, ускорение менялось согласно уравнению зависимости 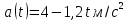 |