Интересные логические задачи. задачки из разных тестовых. За круглым столом сидят 12 человек. Каждый из них говорит Мой сосед справа лжец. Сколько среди них лжецов
 Скачать 120.25 Kb. Скачать 120.25 Kb.
|
|
Задание 1 За круглым столом сидят 12 человек. Каждый из них говорит: «Мой сосед справа — лжец». Сколько среди них лжецов? Если каждый утверждает, что сосед справа лжец, то все 12 человек не могут быть лжецами, иначе все бы говорили правду. Однако, правду все тоже не могут говорить. предположим, что первый человек за столом сказал правду, тогда его сосед справа лжец. Следующий лжец говорит неправду, а значит его сосед говорит правду и так далее. таким образом получается, что лжецы сидят через 1 человека, следовательно, лжецов половина. 12:2=6 лжецов за столом. Ответ: за столом 6 лжецов. Задание 2 Изобретательный Вася выбрал 2 целых положительных числа, оба больше единицы, а их сумма меньше 100. Маше Вася сказал произведение этих чисел, а Саше — их сумму. После чего у Маши и Саши состоялся разговор: Маша: Я не знаю, какая у тебя сумма. Саша: Ничего удивительного. Я и так знал, что ты этого не знаешь. Маша: Воу! Вот теперь я понимаю, чему равна твоя сумма! Саша: Да, и я теперь знаю твое произведение! Какие числа задумал Вася? Маша говорит: "Я не знаю какая у тебя сумма". На первый взгляд, она не сказала ничего особенного, но на самом деле, она своим ответом отмела немало вариантов. Это значит, что произведение раскладывается в множители не единственным способом (то есть 4 = 2*2 или 6 = 2*3 не подходят, а 12 = 2*6 = 4*3 - подходит). Тем самым, мы получили, что хотя бы одно из выбранных Васей чисел - составное, то есть само по себе должно раскладываться на простые множители. Саша говорит: «Ничего удивительного. Я и так знал, что ты этого не знаешь." Это значит, что его сумма чисел не может быть разложена в простые слагаемые, иначе существовала бы вероятность, что Маша поняла бы, какая у Саши сумма. 4 = 2+2, 5 = 2+3, 6 = 3+3, 7 = 2+5 и тд. Обратим внимание, что если бы у Саши была бы сумма четной, то согласно проблеме Гольдбаха: "Каждое чётное число, большее двух, можно представить в виде суммы двух простых чисел." Значит, достаточно рассмотреть все нечетные числа. Но тогда нас интересует только вариант "2+k", где k - число, на 2 меньше, чем наше, но той же четности (то есть нечетное). Тогда оно может быть как простым, так и нет. Тогда мы получаем список всех потенциально подходящих нам чисел в качестве суммы у Саши: 11, 17, 23, 27, 29, 35, 37, 41, 47, 51, 53, 55, 57, 59, 65, 67, 71, 77, 83, 87, 89, 93, 95, 97 . Далее учитываем тот факт, что после этого Маша поняла, какая у Саши сумма, а Саша сразу понял, какое у Маши произведение. Возьмем, например, 11. Его можно разложить на слагаемые как: 2+9, 3+8, 4+7 и 5 +6 для 2 и 9 произведение будет 18. Оно раскладывается на множители как 2 и 9 или 3 и 6. Но если задуманы были 3 и 6, тогда сумма 3 и 6 = 9.Что не подходит, так как 9 можно получить сложением простых чисел 2 и 7 для 3 и 8 произведение будет 24. Оно также раскладывается на множители как 12 и 2 или 4 и 6. 6+4 - четная сумма, не подходит. 12=2 также четная сумма. для 4 и 7 произведение будет 28, оно также раскладывается на множители как как 2 и 14, но опять же, четная сумма. Для 5 и 6 произведение будет 30. Также раскладывается на 2 и 15 или на 3 и 10. И тоже нечетная сумма. Значит, если у Маши задумано произведение 30, то тогда она не может угадать сумму у Саши. Итого, для суммы 11 получилось 3 варианта произведения: 2 и 9, 3 и 8, 34 и 7. Но нам нужно, чтобы для одной суммы была только одна пара (иначе Саша не поймет произведение). Получается, число 11 нам не подходит. Отбрасываем. Таким образом проверим все числа из списка и получается, что 17 - единственное, удовлетворяющее условию 17 = 2+15 = 3+14 = 4+13 = 5+12 = 6+11 = 7+10 = 8+9 2+15: 30 = 3*10 (не подходит) = 2*15 (подходит) = 5*6 (подходит) отбрасываем 3+14:42 = 2*21 (подходит) = 3*14 (подходит) = 6*7 (не подходит) отбрасываем 4+13: 52 = 2*26 (не подходит) = 3*13 (подходит) 5+12: 60 = 2*30 (нет) = 3*20 (да) = 6*10 (нет) = 5*12 (да) отбрасываем 6+11: 66 = 6*11 (да) = 3*22 (нет) = 2*33 (да) отбрасываем 7+10: 70 = 7*10 (да) = 5*14 (нет) = 2*35 (да) отбрасываем 8+9: 72 = 8*9 (да) = 2*36 (да) = 4*18 (нет) = 3*24 (да) = 6*12 (нет) отбрасываем. Получается, для суммы 17 подходит всего одна пара чисел - это 4 и 13. Задание 3. У нас есть 2 хрустальных шара и здание высотой в 100 этажей. Известно, что при броске, начиная с этажа K, шары разбиваются. Узнайте этаж K за наименьшее количество бросков. Все этажи здания делим на неравные группы. Пусть таких групп получилось К. Первая, самая нижняя группа содержит N этажей. Бросаем шарик с верхнего этажа этой группы. Если он разбился - бросаем второй шарик с нижнего этажа этой группы (т.е. с первого), и последовательно повторяем броски поднимаясь на один этаж. Если шарик с верхнего этажа не разбился - идем на верхний этаж второй группы. Одна попытка уже использована, поэтому во второй группе должно быть на один этаж меньше, т.е N-1. Рассуждая анологично, в третью группу включим N-2 этажа, в четвертую N-3 и т.д. Общее количество этажей равно N+(N-1)+(N-2)+(N-3)+... +(N-К+1) Сумма этой арифметической прогрессии равна (2N-K+1)K/2 и равна 100. (2N-K+1)K/2=100, откуда N=100/K+K/2- 1/2 Ищем минимум этой функции, для чего продиффернцируем N по К и приравняем производную к нулю. dN/dK=-100/K^2 + 1/2 = 0 Получается, что К равно квадратному корню из 200, т.е 14 (в целых числах) Т.е. в первой группе 14 этажей. Максимальное возможное количество бросаний равно, соответственно, тоже 14 (для любого этажа любой группы, вплоть до сотого).             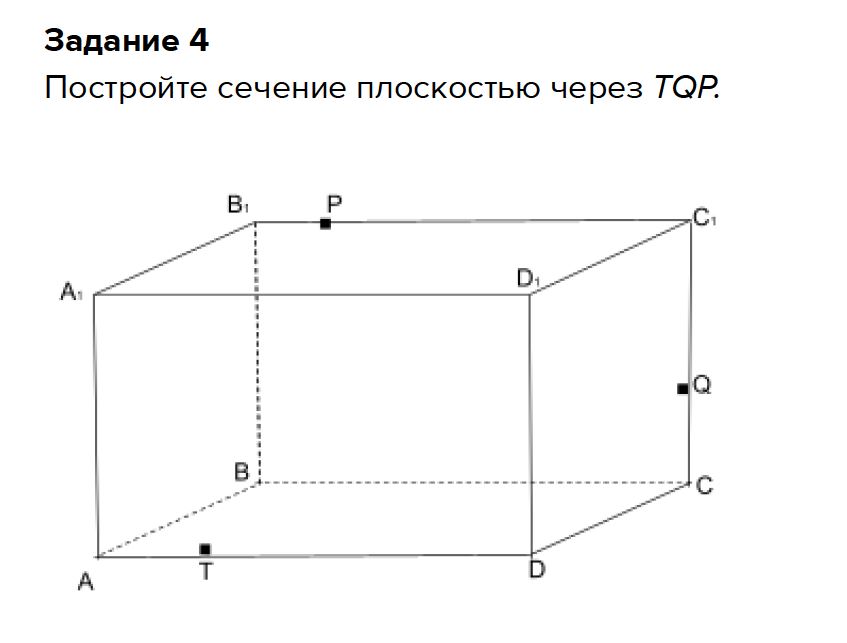       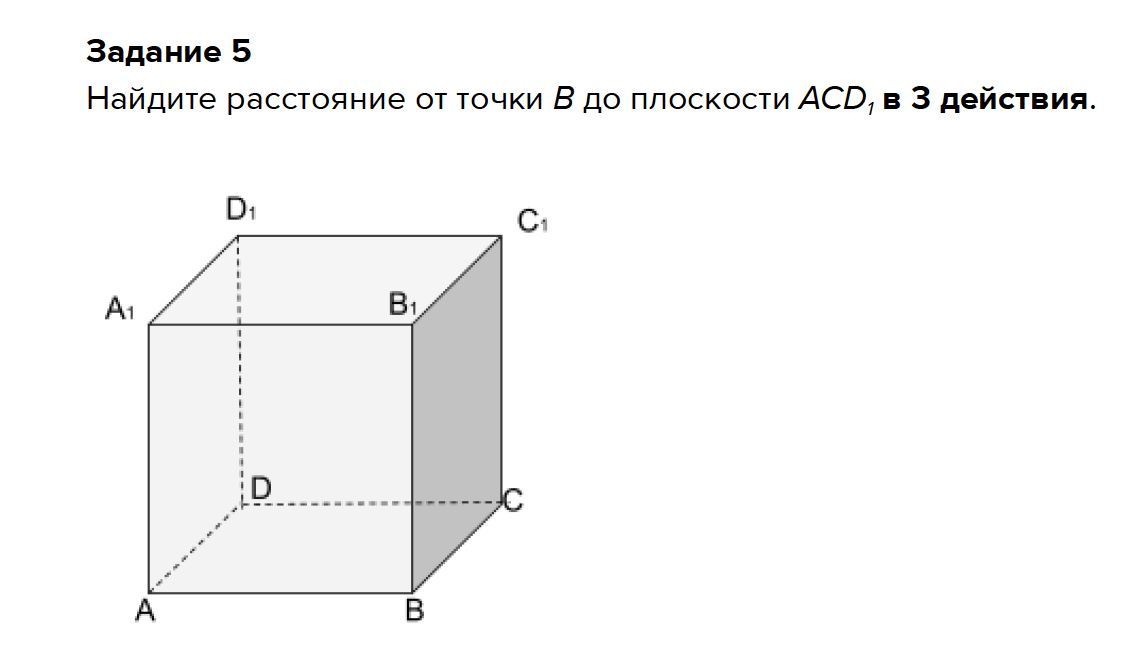 Нужно провести диагональ основания от точки D до B Мы получим точку О, через которую проходит плоскость, перпендикулярная к заданной. 2. Проводим прямую D1O, которая будет являться линией пересечения заданной плоскости и плоскости, перпендикулярной к ней. 3. Проводим отрезок ВЕ, перпендикулярный к D1O. Задание 6. 1-2 2-3 3-3 |
