Теория информационных процессов и систем -. Задача Расчет статически неопределимого составного стержня, работающего на растяжениесжатие
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
Рис. 21. Расчетная схема балки. Эпюры поперечных сил и изгибающих моментов По эпюре Mz находим опасное сечение балки - сечение, в котором изгибающий момент максимален по абсолютной величине. Для заданной балки изгибающий момент в опасном сечении = Mz(2a)=1,5qa2 или после подстановки числовых значений =1,5∙10∙12= 15кНм. Из условия прочности определим требуемый момент сопротивления сечения Номер двутавра находим по расчетному значению момента сопротивления Wz, используя таблицы сортамента прокатной стали. Внимание! В таблицах сортамента прокатной стали (см. «справочные данные») оси z соответствует ось x , это означает, что Wz=Wx. Наиболее близок к требуемому момент сопротивления двутавра №14, равный Wx= 81,7 см3. Выбрав это сечение, определяем нормальные напряжения в поперечном сечении балки: Подбираем прямоугольное сечение, момент сопротивления которого определяется с учетом того, что h=2b: Отсюда 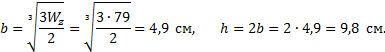 Круглое поперечное сечение имеет момент сопротивления Диаметр круга 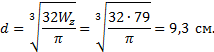 Рассмотрим второй метод построения эпюр внутренних усилий, действующих в сечениях балки. Он состоит в том, что поперечные силы и изгибающие моменты вычисляются на границах участков без записи уравнений Q(z), M(z), а соответствующие эпюры строятся на основании дифференциальных зависимостей между Q, M, q: Зависимости (1) позволяют установить следующие характерные особенности эпюр поперечных сил и изгибающих моментов: На участках, где нет распределенной нагрузки, эпюра Q ограничена прямыми, параллельными оси балки, а эпюра M - наклонными прямыми. На участках, где приложена равномерно распределенная нагрузка интенсивностью q, эпюра Q ограничена наклонными прямыми, а эпюра M - квадратными параболами, выпуклость которых направлена навстречу вектору равномерно распределенной нагрузки. На участках, где Q >0, изгибающий момент возрастает; если Q<0 - изгибающий момент убывает. В сечениях, где к балке приложены сосредоточенные силы, на эпюре Q будут скачки на величину приложенных сил, а на эпюре M - переломы, острие которых направлено против действия этих сил. В сечениях, где к балке приложены пары сил (сосредоточенные моменты), на эпюре M будут скачки на величину этих моментов. Если на участке балки имеется равномерно распределенная нагрузка и эпюра Q в пределах участка изменяет знак, то в сечении, где Q = 0, на эпюре Mz будет экстремум. Примеры использования дифференциальных зависимостей при расчете балок приводятся ниже |
