Теория информационных процессов и систем -. Задача Расчет статически неопределимого составного стержня, работающего на растяжениесжатие
 Скачать 1.13 Mb. Скачать 1.13 Mb.
|
|
Рис.8 Из условия равновесия находим значение М4: Участок AB (0 z1 l1) (рис. 9, а): Участок BC (0 z2 l2) (рис. 9, б): Участок BC (0 z3 l3) (рис. 9, в): По полученным данным строим эпюру крутящих моментов ЭМ (рис. 8). 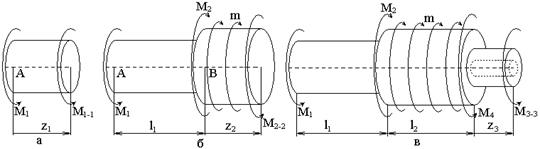 Рис.9 2. Построение эпюры напряжений. Наибольшие напряжения при кручении возникают на внешних волокнах и определяются как где Определим геометрические характеристики сечений: Участок АВ: Участок ВС: Участок CD: Определим опасное сечение, в котором возникают наибольшие напряжения, в долях 1/d3: Участок AB (0 z1 l1): Участок BC (0 z2 l2): 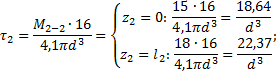 Участок CD (0 z3 l3): По полученным данным строим Э d3 (рис. 8). 3. Расчет на прочность. Подбор сечения. На эпюре Э d3 видно, что опасными являются сечения на участке CD, де действуют наибольшие напряжения. Условие прочности при кручении имеет вид: где – допускаемое касательное напряжение. Примем для материала Ст30 Тогда условие прочности примет вид: Из условия прочности находим оптимальное значение диаметра: 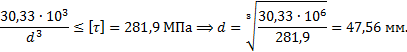 Примем (из ряда Ra40 по ГОСТ 6636-69) d=48 мм. Определим напряжения, действующие в сечениях при выбранном значении d. Участок AB: Участок BC: 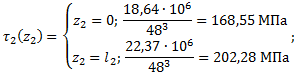 Участок CD: Задача № 8. Подбор сечения деревянной балки при плоском поперечном изгибе 1. Изобразить в масштабе расчетную схему балки в соответствии с исходными данными, выбранными по шифру из таблицы. На схеме должны быть показаны реальные направления заданных нагрузок и их абсолютные числовые значения. Отличные от нуля сосредоточенные силы, попадающие на опоры, учитывать не нужно. 2. Найти опорные реакции. 3. Построить в масштабе эпюры поперечных сил и изгибающих моментов. 4. Изобразить фасад балки и ее сечение. Построить эпюры нормальных и касательных напряжений и показать опасные точки на фасаде и в сечении. 5. Из условия прочности по нормальным напряжениям подобрать размеры сечения. Диаметр бревен не должен превышать ходового размера 26 см. Если это условие выполнить невозможно, подобрать сечение из нескольких бревен (брусьев). 6. Проверить прочность балки по касательным напряжениям, считая [τ] = 2 МПа.
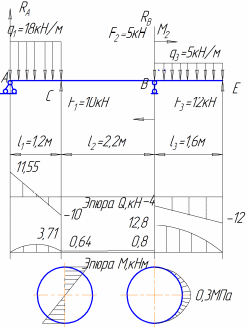 ) Для определения σ(К), τ(К) и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax: 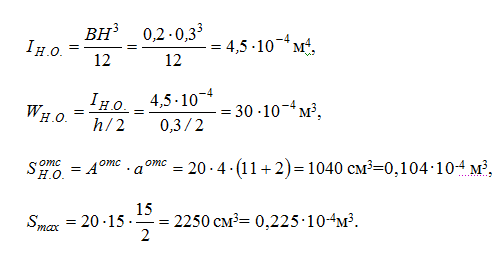 Тогда: 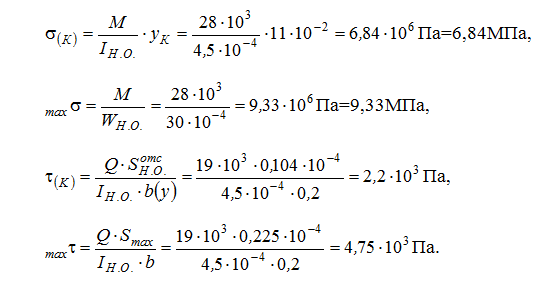 б) Проверка прочности: — по условию прочности нормальных напряжений: 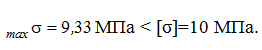 — по условию прочности касательных напряжений: 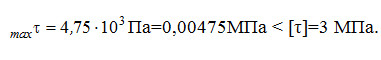 Задача 2 В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см. 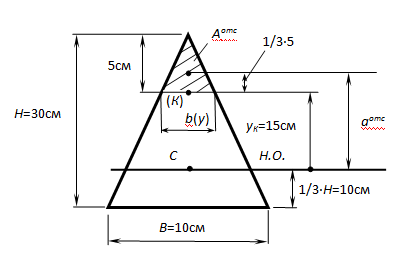 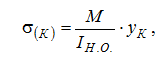 где где 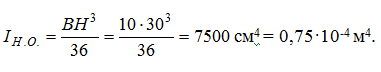 Тогда 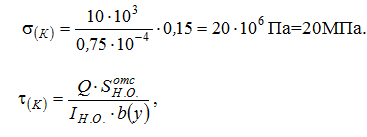 где: где: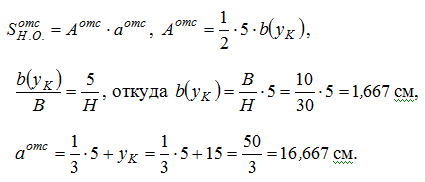 Тогда Тогда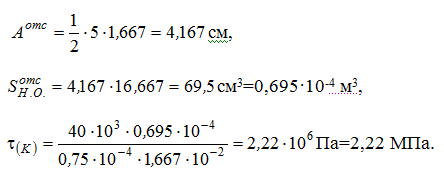 Задача № 9. Подбор сечения стальной двутавровой балки при плоском поперечном изгибе 1. Изобразить в масштабе расчетную схему балки в соответствии с исходными данными, выбранными по шифру из таблицы. На схеме должны быть показаны реальные направления заданных нагрузок и их абсолютные числовые значения. Отличные от нуля сосредоточенные силы, попадающие на опоры, учитывать не нужно. 2. Найти опорные реакции. 3. Построить в масштабе эпюры поперечных сил и изгибающих моментов. 4. Изобразить фасад балки и ее сечение. Построить эпюры нормальных и касательных напряжений и показать опасные точки на фасаде и в сечении. 5. Из условия прочности по максимальным нормальным напряжениям подобрать номер двутавра. 6. Проверить прочность в остальных опасных точках. Если условие прочности в какой-нибудь точке не будет выполняться, подобрать другой номер двутавра.
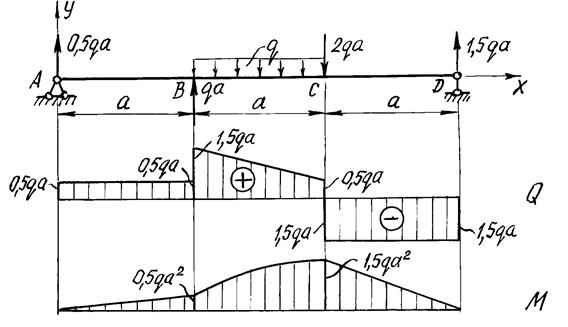
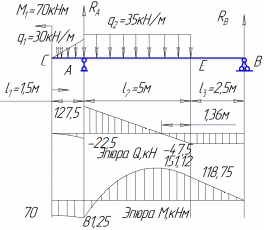 Определение опорных реакций. На схеме показываем опорные реакции R1, H, R2 . Вертикальные реакции направляем вверх и записываем уравнения равновесия: ΣX=0; H=0; ΣMD=0; R13a+qa∙2a-qa∙1,5a-2qa∙a=0. Отсюда R1=0,5qa. ΣMA=0; R23a-2qa∙2a-qa∙1,5a+qa∙a=0. Отсюда R2=1,5qa. Проверим правильность вычислений, составив еще одно уравнение равновесия: ΣY=0; 0,5qa+qa-qa-2qa+1,5qa=0. Условие равновесия удовлетворяется, реакции определены правильно. 2.Построение эпюры Q. Мысленно разбиваем балку на участки. Границами участков являются сечения, в которых к балке приложены сосредоточенные силы или пары сил, начинаются или заканчиваются распределенные нагрузки, имеются промежуточные шарниры. В рассматриваемой балке граничными сечениями будут сечения A, B, C и D. Для каждого из трех участков запишем аналитическое выражение Q(x). Участок AB, 0 Q(x)=R1=0,5qa. Поперечная сила не зависит от переменной x на протяжении всего участка, следовательно, эпюра Q ограничена прямой, параллельной оси абсцисс. Отложив от оси эпюры вверх в выбранном масштабе 0,5qa (рис.21), строим эпюру на этом участке. Участок BC, a Q(x)=0,5qa+qa-q(x-a)=1,5qa-q(x-a). Полученное выражение является уравнением наклонной прямой, которая может быть построена по двум лежащим на ней точкам. Для ее построения найдем значения поперечной силы на границах участков балки x=a, Q(a)=1,5qa, x=2a, Q(2a)=0,5qa. Участок CD, 2a Q(x)=0,5qa+qa-qa-2qa=-1,5qa. Так как поперечная сила не зависит от переменной x, на последнем участке эпюра Q ограничена прямой, параллельной оси балки (см. рис. 21). 3. Построение эпюры Mz. Аналитическое выражение для вычисления изгибающего момента в сечении x необходимо записать для каждого участка балки. Участок AB: Mz(x)=0,5qa∙x. На этом участке балки изгибающий момент возрастает по линейному закону и эпюра Mz ограничена наклонной прямой. Вычисляя его значения в сечениях на границах участка, строим в масштабе (рис. 21) эпюру Mz на сжатом волокне x=0, Mz(0)=0; x=a, Mz(a)=0,5qa2. Участок BC: Полученное уравнение является уравнением квадратной параболы и, поскольку поперечная сила Q на участке BC не изменяет знак, экстремума на эпюре Mz не будет. Определим изгибающий момент на границах участка: x=a, Mz(a)=0,5qa2; x=2a, Mz(2a)=0,5qa∙2a+qa(2a-a)- Отложив вверх от оси балки найденные значения, проводим квадратную параболу выпуклостью вверх (навстречу вектору усилия равномерно распределенной нагрузки). УчастокCD: Mz(x)=0,5qa∙x+qa(x-a)-qa(x-1,5a)-2qa(x-2a). В пределах последнего участка балки (2a При x=2a, Mz(2a)=1,5qa2, при x=3a, Mz(3a)=0. Эпюры Q и Mz показаны на рис. 21.
 |
