Теория информационных процессов и систем -. Задача Расчет статически неопределимого составного стержня, работающего на растяжениесжатие
 Скачать 1.13 Mb.
|
|
Задача № 3. Расчет статически неопределимого составного стержня, работающего на растяжение-сжатие 1. Изобразить в масштабе расчетную схему к задаче в соответствии с исходными данными, выбранными по шифру из таблицы. 2. Проверить, закроется ли зазор под действием приложенной нагрузки. 3. Изобразить расчетную схему с закрытым зазором, показать план сил и составить уравнения равновесия, записав их через внутренние усилия в сечениях. 4. Обозначить на расчетной схеме перемещения сечения, разделяющего растянутый и сжатый участки, и составить условия совместности деформаций. 5. Уравнения равновесия и условия совместности деформаций дополнить соотношениями закона Гука. 6. Из полученной системы уравнений определить продольные усилия в каждой части стержня от заданной нагрузки F. Построить эпюру усилий. 7. Вычислить соответствующие найденным ранее продольным усилиям нормальные напряжения и проверить прочность стержня. Если условие прочности не выполняется, то уменьшить силу Fдо допустимого значения. 8. Построить новую эпюру усилий для скорректированного значения нагрузки. Построить эпюру напряжений от принятой нагрузки F. 9. Выполнить аналогичный расчет на температурное воздействие T. Дано:  :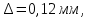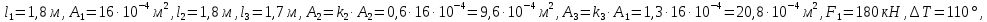
 Заменим действие опор на стержень реакциями ( и ) и составим уравнение проекций сил на ось стержня (ось ): ; , (1) 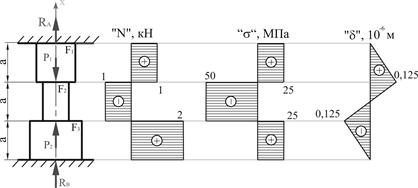 Рис. 1 Остальные уравнения статики дадут нам такое же выражение (1). В одно уравнение входят два неизвестных усилия ( и ), следовательно, задача один раз статически неопределима. Для расчета таких систем необходимо использовать уравнения, содержащие деформации элементов конструкций. Так как концы стержня жестко закреплены, то общая длина не изменяется: . Общая деформация стержня будет складываться из деформаций его элементов: , (2) где – продольное усилие на -том участке; – длина - того участка; – модуль продольной упругости материала; – площадь поперечного сечения - того участка. Выразим продольные усилия в поперечных сечениях стержня через одну из неизвестных реакций . Разделим стержень на участки по местам приложения сосредоточенных нагрузок и местам изменения поперечного сечения стержня. Для приведенной схемы получаем три участка (рис. 1). Мысленно рассечем первый участок произвольно взятым поперечным сечением и отбросим нижнюю часть балки, заменяя ее действие на верхнюю часть продольной силой , которую первоначально направляем в сторону растяжения рассматриваемого элемента первого участка (рис. 2). 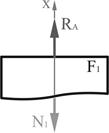 Рис. 2 Из условия равновесия: ; (3) 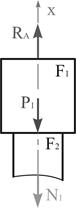 Рис. 3 Мысленно рассечем второй участок произвольно взятым поперечным сечением и отбросим нижнюю часть балки, заменяя ее действие на верхнюю часть продольной силой которую первоначально направляем в сторону растяжения рассматриваемого элемента первого участка (рис. 3). Из условия равновесия: ; (4) Для третьего участка (рис. 3): ; (5) 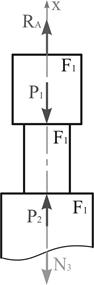 Рис. 4 Деформация участков согласно формуле (2): (6)  (7) (8)Общая деформация должна равняться нулю:  Умножив обе части уравнения на получим:  ,или: . Из выражения (1): (9) Знак «-» указывает на обратное направление реакции . Определяем значения осевых усилий для каждого участка по найденным ранее выражениям (3) – (5): ; ; . По полученным значениям строим эпюру осевых усилий. Для этого проводим нулевую (базовую) линию параллельно оси стержня, перпендикулярно которой будем в масштабе откладывать значения осевых усилий (рис. 1). В одну сторону откладываем положительные значения, в другую - отрицательные. Эпюра заштриховывается перпендикулярно нулевой линии, а внутри эпюры ставится знак откладываемой величины. Рядом указываются значения откладываемых величин. Рядом с эпюрой в кавычках указывается название эпюры (« ») и через запятую - единицы измерения (кН). Нормальные напряжения в поперечных сечениях: (10)  ; ; .По полученным значениям нормальных напряжений строим эпюру нормальных напряжений (« ») (рис. 1). Определим деформацию каждого участка:  ; ; .Эпюру перемещений строим по перемещениям точек , , , . Сечение в точке возьмем как базовое, перемещение которого . Тогда перемещение точки будет равно удлинению первого участка: Перемещение точки будет складываться из перемещения точки и удлинения второго участка:  Перемещение точки будет складываться из перемещения точки и удлинения второго участка: Перемещение является своего рода проверкой правильности решения данной задачи, так как точка принадлежит неподвижной опоре. По полученным значениям строим эпюру перемещений (« ») (рис. 1). Так как внутри участков перемещения поперечных сечений имеют пропорциональную зависимость от координаты сечения , значения, отложенные в точках , , , , соединяются между собой прямыми линиями. Задача № 5. Расчет статически неопределимой шарнирно-дисковой конструкции со стержнями, работающими на растяжение-сжатие 1. Изобразить в масштабе расчетную схему к задаче в соответствии с исходными данными, выбранными по шифру из таблицы. На расчетной схеме должны быть обозначены все силовые и геометрические параметры в их числовом выражении. 2. Подобрать сечения стержней расчетом по упругой стадии деформации (по допускаемым напряжениям): - выделить объект равновесия, показать план сил и составить необходимые уравнения равновесия; - изобразить план перемещений и составить условие совместности деформаций; - дополнить уравнения равновесия и условие совместности деформаций законом Гука и решить полученную систему уравнений относительно усилий в стержнях; - выразить напряжения через неизвестные площади сечений, сравнить их и из условия прочности наиболее напряженного стержня определить необходимые площади сечений. 3. Подобрать сечения стержней расчетом по предельному пластическому состоянию. Сравнить с предыдущим вариантом расчета. 4. Для сечений, подобранных по допускаемым напряжениям, определить дополнительные напряжения, вызванные неточностью изготовления i-того стержня. Сравнить с напряжениями от заданной нагрузки.
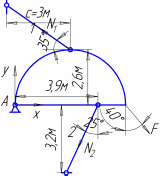 В шарнирно-неподвижной опоре А возникают реакции RА и НА. В стержнях 1 и 2 возникают усилия N1 и N2. Применим метод сечений. Замкнутым разрезом вырежем среднюю часть системы. Жесткую балку покажем схематично — линией, усилия N1 и N2 направим от сечения. 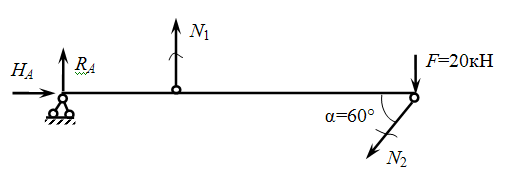 Составляем уравнения равновесия 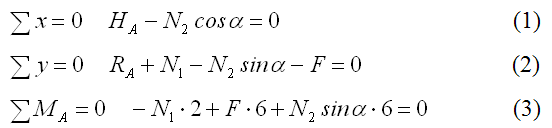 Количество неизвестных превышает количество уравнений статики на 1. Значит, система один раз статически неопределима, и для её решения потребуется одно дополнительное уравнение. Чтобы составить дополнительное уравнение, следует рассмотреть схему деформации системы. Шарнирно-неподвижная опора А остается на месте, а стержни деформируются под действием силы. Схема деформаций 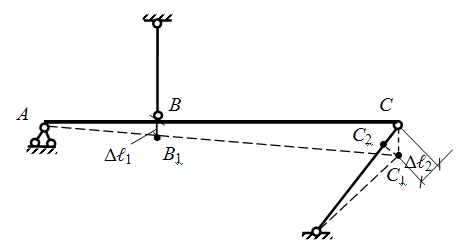 По схеме деформаций составим условие совместности деформаций из рассмотрения подобия треугольников АСС1 и АВВ1. Из подобия треугольников АВВ1 и АСС1 запишем соотношение: 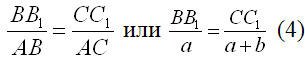 , где ВВ1=Δℓ1 (удлинение первого стержня)Теперь выразим СС1 через деформацию второго стержня. Укрупним фрагмент схемы. 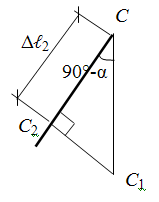 Из рисунка видно, что СС2 = СС1·cos (90º-α)= СС1·sinα. Но СС2= Δℓ2 , тогда Δℓ2= СС1·sinα, откуда: 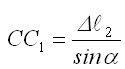 Превратим условие совместности деформации (4) в уравнение совместности деформации с помощью формулы Гука для деформаций. При этом обязательно учитываем характер деформаций (укорочение записываем со знаком «-», удлинение со знаком «+»). 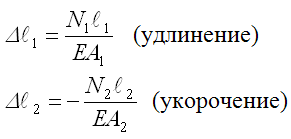 Тогда уравнение совместности деформаций будет: 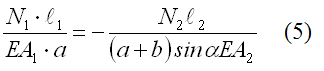 Сокращаем обе части на Е, подставляем числовые значения и выражаем N1 через N2 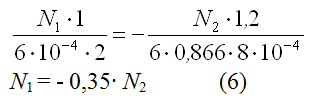 Подставим соотношение (6) в уравнение (3), откуда найдем: N1 = 7,12кН (растянут), N2 =-20,35кН (сжат). Определим напряжения в стержнях. 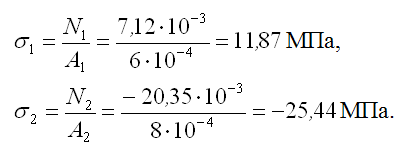 Задача № 6. Исследование напряженно-деформированного состояния в точке тела 1. Изобразить расчетный элемент к задаче в соответствии с исходными данными, выбранными по шифру из таблицы. На гранях элемента должны быть показаны реальные направления заданных напряжений и их абсолютные числовые значения. 2. Найти нормальное и касательное напряжения, действующие по заданной наклонной площадке. Выполнить это аналитически (по формулам) и графически (с помощью круга Мора), сравнить результаты. Показать эти напряжения на наклонной площадке в числовом выражении. 3. Найти положение главных площадок и действующие по ним главные напряжения. Выполнить это также двумя способами. 4. Найти наибольшие в точке касательные напряжения и показать площадки, по которым они действуют. 5. Проверить прочность материала в рассматриваемой точке по соответствующим материалу теориям прочности. Для каждой рассмотренной теории вычислить фактический коэффициент запаса. Показать опасные площадки. 6. Найти величины относительных продольных деформаций по главным направлениям и вычислить относительную объемную деформацию.
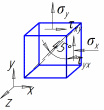 Аналитический способ исследования напряженного состоянияОпределение напряжений на наклонной площадке. Напряжения, действующие на наклонной площадке (см. рис. 2), находим по формулам  (1)и . (2) В этих формулах положение площадки задает угол между нормалью n к площадке и осью . Этот угол нельзя путать с углом , указанным на рис. 1. Можно отсчитывать угол не от оси , а от оси z, но тогда в формулах (1) и (2) напряжения , надо поменять местами и напряжение заменить напряжением . Надо выбирать более удобный способ. Используем угол между n и осью , отсчитывая его от оси к нормали n: (см. рис. 2). Значение угла положительное, так как угол отсчитывается против часовой стрелки. Согласно формулам (1) и (2) 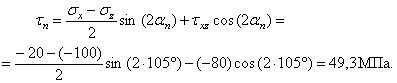  , Получившееся нормальное напряжение отрицательно, значит, оно направлено к площадке (сжимающее). Касательное напряжение положительно, это значит, что оно обходит площадку по часовой стрелке. Используем теперь угол между нормалью n и осью , отсчитывая его от z к n: . Формулы (1) и (2) записываем в измененном виде: 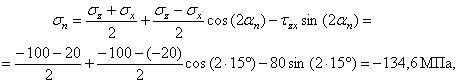 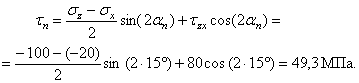 Абсолютная величина полного напряжения (или просто полное напряжение)  Вычисленные напряжения показаны на рис. 3. 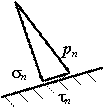 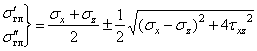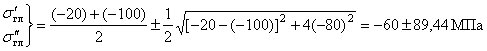Рис.3 Определение главных напряжений и главных направлений.Согласно  главные напряжения .После вычисления главные напряжения следует пронумеровать согласно убыванию. Чтобы не путать напряжения до и после нумерации, специально используются для этих напряжений разные обозначения. Главные напряжения, пронумерованные согласно их величине, , , . Найдем положение главных площадок. Сказанное о способах вычисления напряжений по наклонной площадке относится и к способам вычисления положения главных площадок. Здесь мы вычислим углы , , определяющие положения главных площадок, одним способом: будем отсчитывать эти углы от направления оси . Углы являются решениями уравнения :  ,то есть Получены два значения угла, которые отвечают площадкам с напряжениями , (рис. 4). Выясним, какому из этих напряжений соответствует угол . Для этого определим по формуле 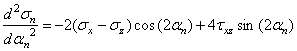 знак второй производной при : . 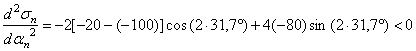Рис.4 Знак отрицательный, следовательно, по этой площадке действует бoльшее из найденных главных напряжений – напряжение . Теперь можно в соответствии с нумерацией главных напряжений пронумеровать и углы: , . Определение максимального касательного напряжения. Касательное напряжение, максимальное среди касательных напряжений на площадках, перпендикулярных плоскости (рис. 5), определяется формулой :  МПа. Рис.5 В рассматриваемом примере главные напряжения , , поэтому касательное напряжение является максимальным среди касательных напряжений для всей совокупности площадок, проходящих через заданную точку: . Нормальные напряжения на той же площадке даются формулой:  МПа.Графический способ исследования напряженного состояния Круг напряжений Мора является средством вычисления. При выполнении задачи его необходимо построить в крупном масштабе на миллиметровке, используя заточенный карандаш. Чем точнее выполнены построения, тем точнее будет получен результат. Строим круг напряжений Мора (рис. 6). Изображаем систему координат с одинаковым масштабом по вертикальной и горизонтальной осям. Отмечаем на координатной плоскости две точки X, , соответствующие заданным площадкам с нормалями . Координатами точек , являются нормальные и касательные напряжения на заданных площадках. Соединяем точки отрезком, который представляет собой диаметр круга Мора. Точка О пересечения диаметра с осью – центр круга. Проводим окружность.  Рис.6 Точкам I, III пересечения круга с горизонтальной осью соответствуют главные площадки 1, 3. Горизонтальные координаты этих точек (измеренные в масштабе) являются главными напряжениями: МПа, МПа. Углы , , определяют положения главных площадок. Отмеченные на рисунке углы дают удвоенные значения , . По рисунку сразу видно, какому главному напряжению соответствует каждое значение угла. Графически найденные значения: , . Графический способ дает возможность проверить аналитическое решение, поэтому в расчетной работе следует рядом с кругом напряжений на отдельном рисунке показать положения главных площадок и напряжения на них. Площадке, по которой действует максимальное касательное напряжение, соответствует точка круга. Координаты точки дают значения МПа, МПа. Найдем с помощью круга напряжений напряжения на наклонной площадке. Построим на круге точку , соответствующую наклонной площадке. Для этого отложим от радиуса OX (соответствующего оси x) против часовой стрелки угол , либо от радиуса ОZ (соответствующего оси z) в том же направлении угол . Координаты точки дают напряжения на наклонной площадке: , . Полное представление о напряженном состоянии дают три круга напряжений. Точки каждого круга соответствуют площадкам, которые перпендикулярны одной из главных площадок. Круги строятся по главным напряжениям. Обычно изображение напряженного состояния в виде трех кругов Мора используется в качестве иллюстрации, а не в качестве способа вычисления, поэтому данный рисунок можно выполнить в меньшем масштабе и не обязательно на миллиметровке. Все три круга напряжений для рассматриваемого напряженного состояния показаны на рис. 7. Построенный на рис. 6 круг напряжений соответствует площадкам, перпендикулярным плоскости чертежа (перпендикулярным второй главной площадке). Из рис. 7 видно, что максимальное касательное напряжение определяется по бoльшему кругу.  Рис.7 Проверка прочности. Главные напряжения , , уже известны (вычислены выше). Начать решение вопроса нужно с выбора соответствующей материалу теории прочности. По условию задачи материал – сталь (пластичный материал), поэтому используем третью и четвертую теории прочности. Согласно третьей теории прочности эквивалентное напряжение . Сравнение с пределом текучести показывает, что материал работает упруго. Действительно, . Но условие прочности не выполнено: . Это означает, что не обеспечен нормативный коэффициент запаса прочности. Конструкцию, имеющую точку с такими напряжениями, эксплуатировать запрещается. Действительный (фактический) коэффициент запаса меньше нормативного . Согласно четвертой теории прочности 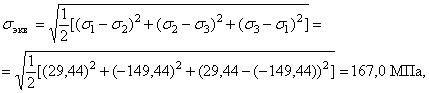 МПа. Условие прочности не выполнено и согласно четвертой теории. Однако фактический коэффициент запаса оказывается другим: . Положения опасных площадок согласно третьей и четвертой теориям приведены на рис. 8 и рис.9. 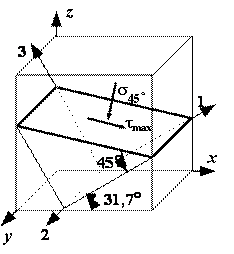  Рис.8 Рис.9 По площадке, показанной жирной линией на рис. 8, действует максимальное касательное напряжение. Эта площадка перпендикулярна к площадке 2 и наклонена под углом в 45° к площадкам 1 и 3. Площадка, показанная жирной линией на рис. 9, соответствует четвертой теории прочности. Она равно наклонена ко всем трем главным площадкам. Специально обратим внимание на способ изображения опасных площадок: эти площадки показаны с привязкой к исходному элементу. Так необходимо сделать и при оформлении задачи. Положение исходного элемента по отношению к конструкции, из которой вырезан элемент, известно. Примененный способ изображения опасных площадок позволяет указать эти площадки непосредственно на конструкции. Определение деформаций в точке. Следует начать с выяснения, работает ли материал в упругой области. Вычисленное выше эквивалентное напряжение оказалось меньше предела текучести. Это означает, что уровень напряжений соответствует упругой стадии деформирования и можно использовать обобщенный закон Гука. Если уровень напряжений соответствует неупругой стадии деформирования, то закон Гука определяет только упругую часть полных деформаций. В задаче при этой ситуации нужно вычислить только упругую составляющую деформации, отметив это примечанием в тексте. Линейные деформации в направлении осей  , , .Угловая деформация  .Знак минус означает, что угол уменьшается. Две другие угловые деформации отсутствуют: , так как равны нулю соответствующие касательные напряжения. Линейные деформации вдоль главных направлений 1, 2, 3    Относительная объемная деформация . Рис. 10 и рис.11 разъясняют результаты вычислений. Условно исходные длины ребер элемента считаются равными единице. При этом линейные относительные деформации в направлении этих ребер равны абсолютным изменениям длин. В исходном недеформированном состоянии грани элемента параллельны координатным плоскостям системы координат . В результате деформации тела элемент перемещается как жесткое целое и деформируется. На рис. 10 жирной линией изображен деформированный элемент.  Рис.10 Недеформированный элемент показан штриховой линией. Перемещение элемента как жесткого целого не изображено. Этот элемент получает угловые и линейные деформации. Деформированный элемент, грани которого в исходном недеформированном состоянии были параллельны главным площадкам, показан на рис. 11. Этот элемент получает только линейные деформации.  Задача № 7. Подбор сечения составного стержня, работающего на кручение 1. Изобразить в масштабе в аксонометрии расчетную схему стержня в соответствии с исходными данными, выбранными по шифру из таблицы. На схеме должны быть показаны реальные направления заданных нагрузок и их абсолютные числовые значения. 2. Построить в масштабе эпюру крутящих моментов. 3. Для каждого сечения изобразить эпюру касательных напряжений, показать напряженное состояние в опасной точке и подобрать размеры поперечных сечений из условия прочности. 4. Вычислить для каждого участка погонный угол закручивания и проверить условие жесткости. Если оно где-либо не выполняется, подобрать новый размер сечения из условия жесткости. 6. Определить угол закручивания на каждом участке стержня и построить в масштабе эпюру углов закручивания.
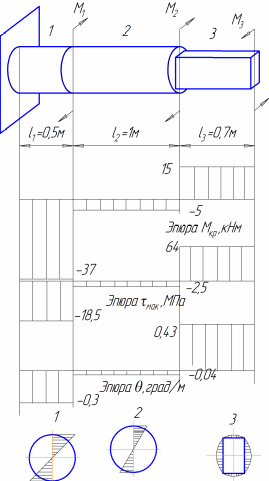 Решение. 1. Построение эпюры крутящих моментов. Направим ось z вдоль оси стержня (рис. 8).  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||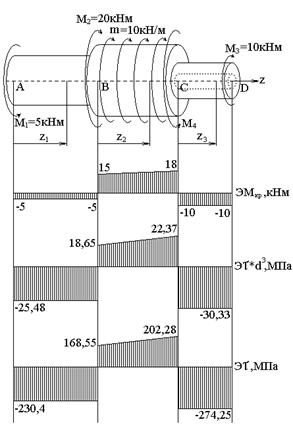
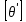, град/м