Теория Игр. теория игр. Задача Составить матрицу выигрышей. Является ли игра антагонистической
 Скачать 50.75 Kb. Скачать 50.75 Kb.
|
|
«Теория игр» Задача № 1. Составить матрицу выигрышей. Является ли игра антагонистической? Разведка боем. Два военных подразделения с целью разведки определенного района могут одновременно выслать либо танк, либо бойцов с противотанковым оружием, либо бойцов-пулеметчиков. Если в этом районе встретятся боевые единицы одинаковых видов, то разведка не состоится, и каждая из сторон ничего не получает. Далее, при встрече разных подразделений: танк побеждает бойцов- пулеметчиков, бойцы-пулеметчики побеждают бойцов с противотанковым оружием, бойцы с противотанковым оружием побеждают танк. Выигрыш оценивается единицей. Решение Задача № 2. Упростить по принципу доминирования и найти седловые точки.
Решение Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков. Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называют выбором стратегии игрока. Если каждый из игроков выбрал свою стратегию, то эту пару стратегий называют ситуацией игры. Следует заметить, каждый игрок знает, какую стратегию выбрал его противник, т.е. имеет полную информацию о результате выбора противника. Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы. 1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 4, которая указывает на максимальную чистую стратегию A5. Верхняя цена игры b = min(bj) = 4. Седловая точка (5, 1) указывает решение на пару альтернатив (A5,B1). Цена игры равна 4. Задача № 3. Решить аналитически игру 2x2. 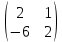 Решение Рассмотрим игру двух лиц, интересы которых противоположны. Такие игры называют антагонистическими играми двух лиц. В этом случае выигрыш одного игрока равен проигрышу второго, и можно описать только одного из игроков. Предполагается, что каждый игрок может выбрать только одно из конечного множества своих действий. Выбор действия называют выбором стратегии игрока. Если каждый из игроков выбрал свою стратегию, то эту пару стратегий называют ситуацией игры. Следует заметить, каждый игрок знает, какую стратегию выбрал его противник, т.е. имеет полную информацию о результате выбора противника. Чистой стратегией игрока I является выбор одной из n строк матрицы выигрышей А, а чистой стратегией игрока II является выбор одного из столбцов этой же матрицы. 1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях. Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = 1, которая указывает на максимальную чистую стратегию A1. Верхняя цена игры b = min(bj) = 2. Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 1 ≤ y ≤ 2. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии). Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получить максимальный средний выигрыш. Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I. 3. Находим решение игры в смешанных стратегиях. Запишем систему уравнений. Для игрока I 2p1-6p2 = y p1+2p2 = y p1+p2 = 1 Для игрока II 2q1+q2 = y -6q1+2q2 = y q1+q2 = 1 Решая эти системы методом Гаусса (решение см. ниже), находим: y = 11/9 p1 = 8/9 (вероятность применения 1-ой стратегии). p2 = 1/9 (вероятность применения 2-ой стратегии). Оптимальная смешанная стратегия игрока I: P = (8/9; 1/9) q1 = 1/9 (вероятность применения 1-ой стратегии). q2 = 8/9 (вероятность применения 2-ой стратегии). Оптимальная смешанная стратегия игрока II: Q = (1/9; 8/9) Цена игры: y = 11/9 Также решение можно найти по следующим формулам: |
