199622 ф-ка. Задача 017 3 Задача 027 5 Задача 037 7 Задача 047 10 Задача 057 12 Задача 067 13 Задача 077 14
 Скачать 109.62 Kb. Скачать 109.62 Kb.
|
|
Содержание Задача 2.017 3 Задача 2.027 5 Задача 2.037 7 Задача 2.047 10 Задача 2.057 12 Задача 2.067 13 Задача 2.077 14 Список использованных источников 17 Задача 2.017Условие: Два точечных заряда q1=-50 нКл и q2=100 нКл находятся на расстоянии d=20 см друг от друга. Определить силу F, действующую на заряд q3=-10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d. Дано: СИ: q1=-50 нКл -5*10-8Кл q2=100 нКл 10-7 Кл d=20 см 0,2 м q3=-10 нКл -10-8 Кл Найти: F-? Решение: Поскольку расстояния между зарядами одинаковы и равны d, то заряды находятся в вершинах равностороннего треугольника. Заряды q1 и q3 имеют одинаковые знаки, поэтому они отталкиваются друг от друга, а сила F1, действующая на заряд q3 со стороны заряда q1, направлена вдоль прямой q1q3 от заряда q1 к заряду q3. Заряды же q2 и q3 имеют разные знаки, поэтому они притягиваются друг к другу, а сила F2, действующая на заряд q3 со стороны заряда q2, направлена вдоль прямой q2q3 от заряда q3 к заряду q2. 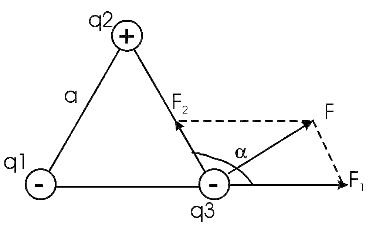 Сила, с которой действует заряд q2 на заряд q3, определяется по закону Кулона: 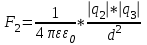 где ε- диэлектрическая постоянная. В нашем случае она равна 1. Сила, с которой действует заряд q1 на заряд q3, определяется по закону Кулона: 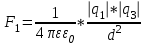 По принципу суперпозиции сила, действующая на заряд q3, является векторной суммой сил, действующих со стороны зарядов q1 и q2, т.е 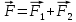 Равнодействующая F сил F1 и F2 находится как диагональ параллелограмма, построенного на силах F1 и F2. Абсолютная величина F этой равнодействующей найдется по теореме косинусов с учетом того, что угол между силами F1 и F2 равен 120°: 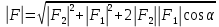 (1) (1)Подставляя силы в формулу (1), получаем: 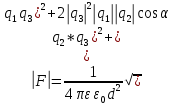 Подставим численные данные: 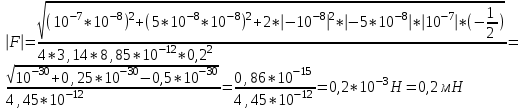 Проверим размерность по формуле (1) 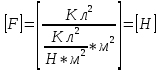 Ответ: F=0,2 мН Задача 2.027Условие: В вершинах квадрата со стороной a=10 см находятся заряды q1=q2=q3=q4= 10 мкКл. Определить напряженность Е и потенциал поля φ, создаваемого этими зарядами в центре квадрата. Дано: СИ: a=10 см 0,1 м q1=q2=q3=q4= 10 мкКл 10-5 Кл Найти: E-? φ-? Решение: 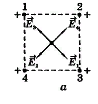 На рисунке изображены векторы Е для поля 4-х одноименных зарядов. Напряженность 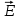 поля, создаваемого системой зарядов, равна геометрической сумме напряженностей поля, создаваемого системой зарядов, равна геометрической сумме напряженностей  полей, создаваемых каждым из зарядов. полей, создаваемых каждым из зарядов.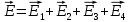 (1) (1)Очевидно, в этом случае в рассматриваемой точке 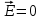 Потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов полей, создаваемых из зарядов. 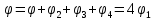 (2) (2)Тогда потенциал поля в центре квадрата выразится формулой: 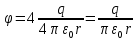 , (3) , (3)Где r – расстояние от центра квадрата до заряда, r= 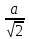 Подставим r в формулу 3: 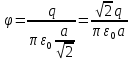 (4) (4)Подставим численные значения в формулу 4: 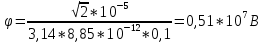 Проверим размерность по формуле (4) 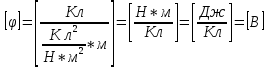 Ответ: Е=0, φ=0,51*107 В Задача 2.037Условие: Шаровой слой, равномерно заряженный по объему с постоянной объемной плотностью ρ = 1 нКл/м3 , имеет внутренний радиус R1 = 3 см и внешний R2 = 5 см. Определить напряженность Е электрического поля в точках, отстоящих от центра шарового слоя на расстояниях r1 = 2 см, r2 = 4 см и r3 = 6 см. Построить график зависимости напряженности Е от r. Дано: СИ: ρ = 1 нКл/м3 10-9 Кл/м3 R1 = 3 см 0,03 м R2 = 5 см 0,05 м r1 = 2 см 0,02 м r2 = 4 см 0,04 м r3 = 6 см 0,06 м Найти: Е-? График Решение: 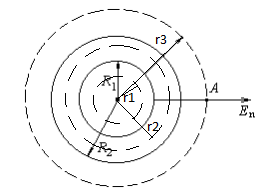 Пространство разделено на три части: 1) 0 < r < R1 (область 1: перед внутренней поверхностью шарового слоя, среда - вакуум); 2) R1 ≤ r ≤ R2 (область 2: внутри шарового слоя, среда - диэлектрик); 3) R2 < r < ∞ (область 3: за наружной поверхностью шарового слоя, среда - вакуум). Согласно теореме Гаусса для диэлектрика, поток вектора D смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов qстор, охватываемых той поверхностью. Возьмём в качестве охватывающей поверхности сферу радиуса r, концентричную шаровому слою. Тогда площадь S её поверхности определяется выражением S = 4πr12, и в области 1 qстор = 0, D * 4πr12 = 0, D = 0; E = D/ε0 = 0; При 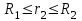 Согласно теореме Гаусса для поля в диэлектрике, поток вектора напряженности электростатического поля: 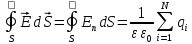 (1) (1)Где En – проекция вектора Е на нормаль n к заряженной плоскости; 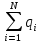 - алгебраическая сумма зарядов, охватываемых произвольной замкнутой поверхностью S/ - алгебраическая сумма зарядов, охватываемых произвольной замкнутой поверхностью S/Найдем заряды, находящиеся внутри поверхности радиуса r2 через объемную плотность заряда: 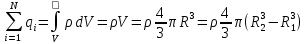 (2) (2)Поток вектора Е через поверхность: 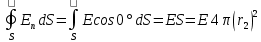 Тогда, по теореме Гаусса: 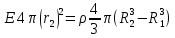 (3) (3)Выразим из формулы 2 напряженность электрического поля: 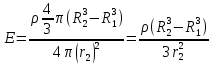 Подставляя напряженность в формулу 1, получим: 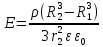 (4) (4)Так как диэлектрик не задан, возьмем ε=2 Подставим численные значения в выражение (4) 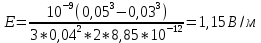 r3>R2 Согласно теореме Гаусса для поля в вакууме, поток вектора напряженности электростатического поля: 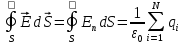 (5) (5)Найдем заряды, находящиеся внутри поверхности радиуса r2 через объемную плотность заряда: 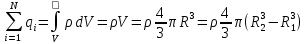 (6) (6)Поток вектора Е через поверхность: 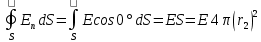 Тогда, по теореме Гаусса: 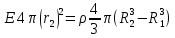 (7) (7)Выразим из формулы 7 напряженность электрического поля: 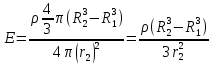 Подставляя напряженность в формулу 5, получим: 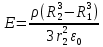 (8) (8)Подставим численные значения в выражение (8) 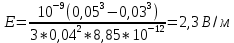 Построим график зависимости Е от r. 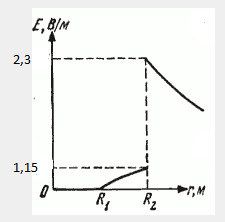 Ответ: 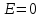 ,Е=1,15В/м, Е=2,3В/м ,Е=1,15В/м, Е=2,3В/мЗадача 2.047Условие: Электрическое поле создано двумя одинаковыми положительными зарядами q1 и q2. Определить работу А сил поля по перемещению заряда q = 10 нКл из точки 1 с потенциалом φ1 = 300 В в точку 2. 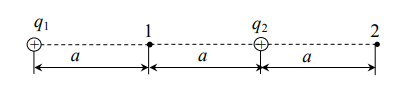 Дано: СИ: q = 10 нКл 10*10-9 Кл φ1 = 300 В Найти: А-? Решение: Работа сил поля определяется соотношением: 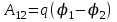 (1) (1)Потенциал точек 1 и 2 выразится формулами: 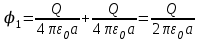 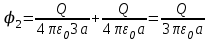 Подставляя выражения для потенциалов в формулу 1, получим: 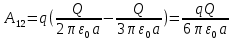 (2) (2)Так как 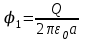 , то формулу 2 запишем в виде: , то формулу 2 запишем в виде: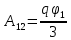 (3) (3)Подставляя, численные значения в формулу 3, получим: 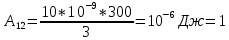 мкДж мкДжПроверим размерность по формуле (3) 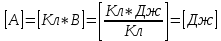 Ответ: 1 мкДж Задача 2.057Условие: Плоский конденсатор заполнен диэлектриком и на его пластины подана некоторая разность потенциалов. Энергия конденсатора в этом случае равна W = 20 мкДж. После того, как конденсатор отключили от источника напряжения, диэлектрик вынули из конденсатора. Работа, которую надо было совершить против сил электрического поля, чтобы вынуть диэлектрик, А = 70 мкДж. Определить диэлектрическую проницаемость ε диэлектрика. Дано: СИ: W = 20 мкДж 2*10-5 Дж А = 70 мкДж 7*10-5 Дж Найти: ε-? Решение: Энергия конденсатора, заполненного диэлектриком, определяется по формуле 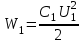 (1) (1)После удаления диэлектрика емкость конденсатора уменьшилась в ε раз и стала равной 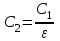 . .Так как заряд конденсатора остался прежним, то разность потенциалов в силу связи 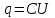 увеличилась в ε раз: увеличилась в ε раз: 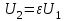 . .Энергия конденсатора после удаления диэлектрика равна: 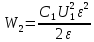 (2) (2)Подставляя в формулу 2, выражение (1) получим: 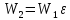 (3) (3)Работа, совершенная против сил кулоновского притяжения, равна 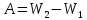 Подставим вместо W2 выражение (3): 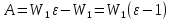 Отсюда выразим диэлектрическую проницаемость: 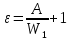 (4) (4)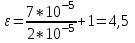 Ответ: ε=4,5 Задача 2.067Условие: К батарее аккумуляторов, ЭДС которой равна 2 В и внутреннее сопротивление r = 0,5 Ом, присоединен проводник. Определить: 1) сопротивление R проводника, при котором мощность, выделяемая в нем, максимальна; 2) мощность Р, которая при этом выделяется в проводнике. Дано: ε=2 В r = 0,5 Ом Найти: R-? P-? Решение: В замкнутой цепи мощность, выделяемая на внешнем участке можно рассчитать по уравнению: 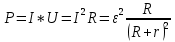 (1) (1)Так как ток в такой цепи рассчитывается по закону Ома 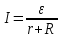 Для расчета максимальной мощности, нужно уравнение (1) продифференцировать по R, приравнять полученное выражение к 0, то есть исследовать функцию на экстремум: 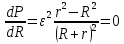 (2) (2)Из уравнения (2) следует r2=R2 или r=R, таким образом, максимальную мощность на внешнем участке цепи можно получить при условии: 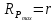 Следовательно, внешнее сопротивление равно внутреннему сопротивлению при Pmax. Из условия задачи 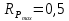 . Это значение подставляем в формулу (1) . Это значение подставляем в формулу (1)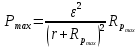 (3) (3)Подставим числовые данные в формулу (3) 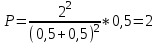 Вт ВтОтвет: R=0,5 Ом, Р=2 Вт. Задача 2.077Условие: На рисунке 1, ЭДС батареи ε = 120 В, сопротивления R3 = 20 Ом и R4 = 25 Ом. Падение напряжения на сопротивлении R1 равно U1 =40 В. Амперметр показывает ток I = 2 А. Определить сопротивление R2. 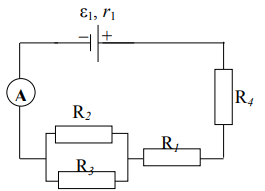 Рис.1 Дано: ε = 120 В R3 = 20 Ом R4 = 25 Ом U1 =40 В I = 2 А Найти: R2-? Решение: Определим неизвестные величины с помощью законов Кирхгофа. Выберем направления токов и обхода контура по часовой стрелке, и представим на рисунке. 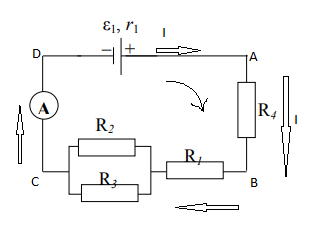 При составлении уравнений по второму закону Кирхгофа соблюдаются следующие правила знаков: а) если ток по направлению совпадает с выбранным направлением обхода контура, соответствующее произведение (I⋅R) входит в уравнение со знаком плюс, в противном случае произведение (I⋅R) входит в уравнение со знаком минус; б) если ЭДС при обходе контура по выбранному направлению приходится идти от минуса к плюсу внутри источника тока, то соответствующая ЭДС входит в уравнение со знаком плюс, в противном случае – со знаком минус. Падение напряжения на параллельном участке цепи U23=ε-U1-U4 (1) Где 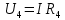 (2) (2)Кроме того U23=U2=U3. Решая, совместно 2 уравнения 1 и 2 U23=ε-U1-IR4 Согласно первому закону Кирхгофа I=I3+I2 (3) Тогда по закону Ома найдем: 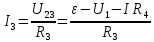 (4) (4)Из формулы 3 выразим I2 и вместо I3 подставим выражение (4) 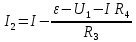 (5) (5)Также по закону Ома 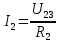 Отсюда выразим R2: 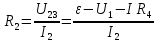 Подставим выражение (5): 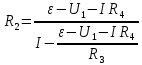 Подставим численные значения: 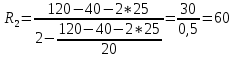 Ом ОмОтвет: R2=60 Ом. Список использованных источниковАнтошина, Л.Г. Общая физика: Сборник задач: Учебное пособие / Л.Г. Антошина, С.В. Павлов, Л.А. Скипетрова . - М.: НИЦ ИНФРА-М, 2012. - 336 c. Кирьянов, А.П. Общая физика. Сборник задач: Учебное пособие / А.П. Кирьянов, С.И. Кубарев, С.М. Разинова, И.П. Шапкарин. - М.: КноРус, 2012. - 304 c. |
