РГР физика. Электростатика Теоретическая часть
 Скачать 315.26 Kb.
|
|
Электростатика 1. Теоретическая часть 1.1 Напряженность и потенциал электростатического поля   где  - сила, действующая на точечный положительный заряд , помещенный в данную точку поля;  - потенциальная энергия этого заряда.1.2 Напряженность и потенциал поля, создаваемого системой зарядов (принцип суперпозиции электростатических полей)   где   - напряженность и потенциал в данной точке поля, создаваемого  -м зарядом.1.3 Напряженность и потенциал поля, создаваемого точечным зарядом   где  - расстояние от заряда до точки поля, в которой определяется напряженность и потенциал.1.4 Напряженность и потенциал поля, создаваемого проводящей (металлической) заряженной сферой радиусом  на расстоянии от центра сферы:а) внутри сферы    б) вне сферы  где - заряд сферы.1.5 Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью или бесконечно длинным цилиндром (вне цилиндра),  где  - линейная плотность заряда; - расстояние от нити или от оси цилиндра до точки, в которой вычисляется напряженность электростатического поля (внутри цилиндра  ).1.6 Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,  где  - поверхностная плотность заряда.7. Графическое изображение электростатических полей. Электростатические поля принято изображать при помощи силовых линий вектора напряженности.   Свойства силовых линий: - вектор напряженности  направлен по касательной к силовой линии;- стрелка на силовой линии указывает направление действия поля на положительный заряд; - силовые линии начинаются и заканчиваются на электростатических зарядах (или в бесконечности); - густота силовых линий прямо пропорциональна модулю вектора напряженности .8. Поток вектора напряженности электростатического поля через любую замкнутую поверхность  (теорема Остроградского – Гаусса) где - суммарный электрический заряд, заключенный внутри замкнутой поверхности .Задание 1. Формулировка задания 1. Рассчитать напряженность и потенциал электростатического поля равномерно заряженный сферической поверхности для точек внутри сферы, на ее поверхности и вне сферы на заданных расстояниях от ее центра.Построить графики зависимостей напряженности и потенциала от расстояния от центра сферы для обеих сред.С помощью силовых линий вектора напряженности графически изобразить электростатическое поле равномерно заряженной сферы и доказать, что аналитическое представление электростатического поля совпадает с графическим. Решение задания. Параметры задания: 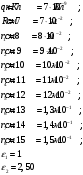 Теорема Остроградского-Гаусса для электростатических полей утверждает, что поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен отношению суммарного электрического заряда , заключенного внутри данной поверхности, к диэлектрической постоянной  . На расстоянии от центра сферы менее  (область I) никаких электрических зарядов нет. Следовательно, напряженность электростатического поля в этой области равна нулю при  . (1)На расстоянии  происходит скачок величины напряженности электростатического поля  от нуля до некоторого значения. В пространстве за пределами сферы (область II) напряженность поля убывает в соответствии с соотношением при  . (2)Определим напряженность электростатического поля в заданных точках, соответствующих расстояниям  .Величина напряженности в первой среде с диэлектрической проницаемостью  в соответствии с выражением (1) в области I  , на границе в этой области  Все точки находятся в области II, и величина напряженности  определяется по формуле (2). На поверхности сферы   Подставив значения, определим  .Проверка размерности используемых формул  .Величина напряженности во второй среде с диэлектрической проницаемостью  в соответствии с выражением (1) в области I .Все точки находятся в области II, и величина напряженности определяется по формуле (2). На поверхности сферы   Подставив значения, определим  .Проверка размерности используемых формул .Потенциал величина непрерывная, т.е. не испытывает скачков на границах. Тогда внутри сферы область I потенциал определим по формуле  (3)вне сферы область II потенциал равен (4)Определим потенциал в первой среде с диэлектрической проницаемость :Внутри сферы и на границе  : Вне сферы  : Проверка размерности используемых формул  .Потенциал во второй среде с диэлектрической проницаемость :Внутри сферы и на границе : Вне сферы : Проверка размерности используемых формул .В соответствии с полученными соотношениями (1), (2), (3) и (4) построим график зависимости напряженности и потенциала электростатического поля от расстояния до центра сфер 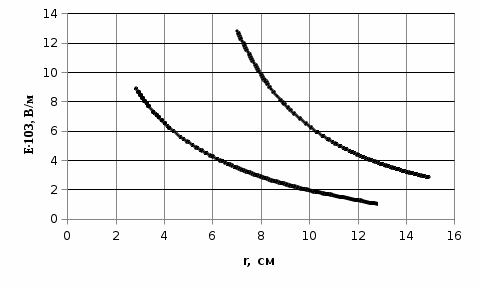 и  для двух сред. Рис. 1. Зависимость напряженности электрического поля от расстояния в первой среде  Рис. 2. Зависимость напряженности электрического поля от расстояния во второй среде 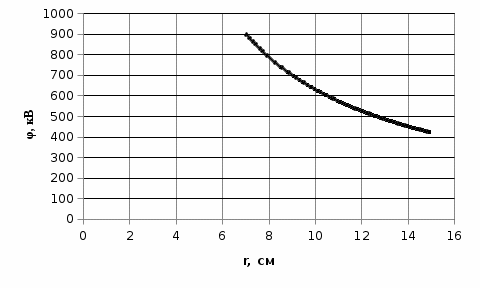 Рис. 3. Зависимость потенциала электрического поля от расстояния в первой среде 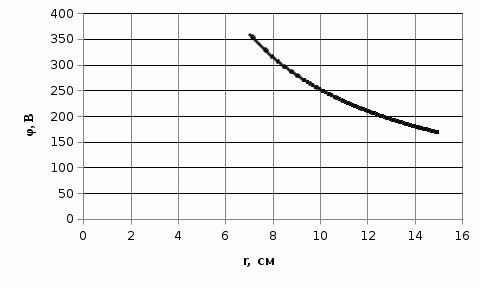 Рис. 4. Зависимость потенциала электрического поля от расстояния во второй среде Силовые линии вектора напряженности электростатического поля, создаваемого равномерно заряженной сферы, начинаются на поверхности сферы и направлены радиально.                R Cледовательно, их густота с расстояние будет убывать, а густота линий определяет абсолютное значение вектора напряженности. Т.о. из графического представления электростатического поля, создаваемого равномерно заряженной сферы, следует, что напряженность поля с расстоянием убывает, что совпадает с аналитическим представлением электростатического поля. Анализ РГР 1. В результате выполнения расчетно-графической работы 1: 1. получены соотношения - (1), (2), (3), (4) - определяющие зависимость напряженности и потенциала электростатического поля и  от расстояния до центра сферической поверхности для двух сред;2. рассчитаны значения напряженности и потенциала электростатического поля во всех заданных точках, соответствующих расстоянию до центра сферической поверхности для двух сред;3. проведена проверка размерности полученных формул для двух сред; 4. построен график зависимости напряженности и потенциала электростатического поля, созданного сферической заряженной поверхностью от расстояния до их центра и для двух сред.5. графически изображено электростатическое поле равномерно заряженной сферы и доказано, что аналитическое представление электростатического поля совпадает с графическим. Задание 2. Формулировка задания 2. Шар радиусом равномерно заряжен с объемной плотностью  . Используя теорему Остроградского - Гаусса, вывести формулу зависимости напряженности электрического поля от расстояния rот центра шара для случая, когда  Построить график зависимости для случая, когда Определить разность потенциалов между двумя точками, лежащими внутри шара на расстояниях  и  от его центра.Решение задания. Параметры задания: 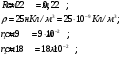 Теорема Остроградского-Гаусса для электростатических полей утверждает, что поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен отношению суммарного электрического заряда , заключенного внутри данной поверхности, к диэлектрической постоянной . Выделим внутри шара сферу произвольного радиуса  , тогда заряд заключенный внутри сферы будет равен  Тогда по теореме Остроградского-Гаусса для электростатических полей имеем 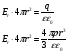 По условию  , имеем что напряженность внутри шара на расстоянии  от центра шара равна (1)Проверка размерности используемых формул  .Используя (1) построим график зависимости 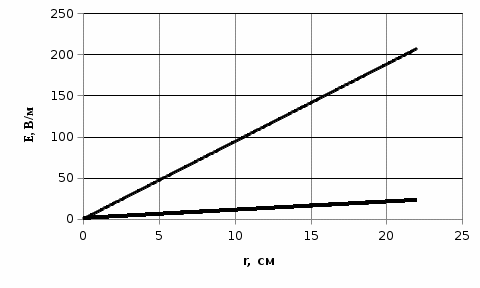для случая, когда  Рис. 1 Зависимость напряженности электрического поля от расстояния внутри шара. Определим разность потенциалов между двумя точками, лежащими внутри шара на расстояниях и от его центра.Связь напряженности электрического поля и потенциал выражается формулой  в случае радиальной или сферической симметрии электростатического поля 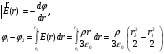 Проверка размерности используемых формул 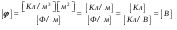 .Тогда подставляем числовые значения  Анализ РГР 2. В результате выполнения расчетно-графической работы 2: 1. получено соотношение - (1) - определяющие зависимость напряженности и потенциала электростатического поля и , созданного внутри равномерно заряженного шара от расстояния до его центра и ;2. построен график зависимости напряженности электростатического поля, созданного внутри равномерно заряженного шара от расстояния до его центра ;3. проведена проверка размерности полученных формул; 4. рассчитаны значения разности потенциала электростатического поля в заданных точках, соответствующих расстоянию до центра сферической поверхности  и  .Задание 3. Формулировка задания 3. Две коаксиальные цилиндрические поверхности (цилиндрический конденсатор) заряжены разноименно с одинаковой линейной плотностью . Рассчитать напряженность электрического поля на расстояниях от оси цилиндров.Построить графики зависимости напряженности электрического поля от расстояния от оси цилиндров, если пространство между цилиндрами заполнено: а) воздухом, б) диэлектриком.Решение задания. Параметры задания:  Теорема Остроградского-Гаусса для электростатических полей утверждает, что поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен отношению суммарного электрического заряда , заключенного внутри данной поверхности, к диэлектрической постоянной . Разобьем расчеты на 3 области. Для каждой области рассчитаем напряженность электрического поля и потенциал, используя теорему Гаусса-Остроградского:  Для этого в каждой области выделим контур высотой  и радиусом  , где индекс  соответствует номеру области. Линии напряженности электрического поля будут направлены радиально, и пронизывать будут только боковую поверхность. Через торцевые стороны поток вектора напряженности будет равен нулю. Поэтому в теореме Гаусса-Остроградского рассматриваем только боковую поверхность.Рассмотрим область 1  . Выделим контур высотой и радиусом  . Площадь боковой поверхности будет равна  , заряд охватываемый контуром будет равен нулю (в этой области нет зарядов). Тогда методом суперпозиций (теорема Гаусса-Остроградского) имеем  Следовательно, в области 1  , (1)На внутренней границе при   Рассмотрим область 2  . Рассуждения аналогичные.   (2)На внешней границе при  На внутренней границе при   Рассмотрим область 3  .Тогда методом суперпозиций (теорема Гаусса-Остроградского) имеем  Следовательно, в области 3  , (3)На внешней границе при  Подставляем числовые значения для среды воздух  :На границах при 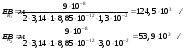 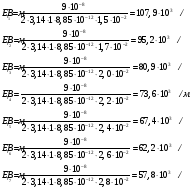и   Подставляем числовые значения для среды диэлектрик  :На границах при 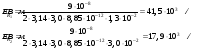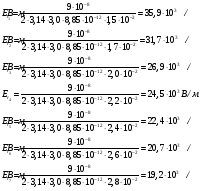и   Проверка размерности используемых формул  .Используя (1), (2) и (3) построим график зависимости 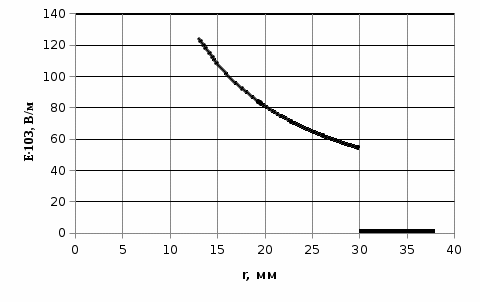для случая, когда  Рис. 1 Зависимость напряженности электрического поля, создаваемого коаксиальными цилиндрами от расстояния от оси цилиндров в воздухе. 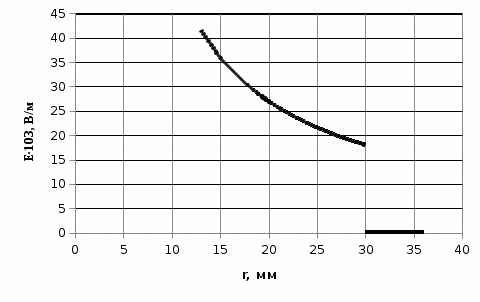 Рис. 2. Зависимость напряженности электрического поля, создаваемого коаксиальными цилиндрами от расстояния от оси цилиндров в диэлектрике. Анализ РГР 3. В результате выполнения расчетно-графической работы 3: 1. получено соотношение - (1), (2) и (3) - определяющие зависимость напряженности электростатического поля , созданного коаксиальными цилиндрами от расстояния от оси цилиндров ;2. рассчитаны значения напряженности и потенциала электростатического поля во всех заданных точках, соответствующих расстоянию до центра сферической поверхности для двух сред;3. построен график зависимости напряженности электростатического поля , создаваемого коаксиальными цилиндрами от расстояния от оси цилиндров в воздухе и диэлектрике;4. проведена проверка размерности полученных формул; Задание 4. Формулировка задания 4. Электростатическое поле создано двумя бесконечными параллельными плоскостями (пластинами), равномерно заряженными с поверхностными плотностями заряда  и  . Расстояние между плоскостями равно  . Найти разность потенциалов между пластинами. Определить напряженность электростатического поля между пластинами и вне пластин. Построить график изменения напряженности электростатического поля вдоль линии, перпендикулярной пластинам. Решение задания. Параметры задания: 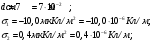 Теорема Остроградского-Гаусса для электростатических полей утверждает, что поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен отношению суммарного электрического заряда , заключенного внутри данной поверхности, к диэлектрической постоянной .
Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, где - поверхностная плотность заряда.Тогда напряженность, создаваемая первой и второй плоскостями соответственно равны:  (1) (2)Плоскости делят все пространство на три области: I, II, III. Как видно из рисунка, в первой и третьей областях электрические силовые линии обоих полей направлены в противоположные стороны, следовательно, результирующее поле в этих областях соответственно равны  (3)Во второй области (между пластинами) электрические силовые линии полей направлены в одну сторону, и, следовательно, напряженность поля  равна сумме напряженностей полей, создаваемых первой и второй плоскостями: (4)Проверка размерности используемых формул .Связь напряженности электрического поля и потенциал выражается формулой Тогда для плоскостей имеем 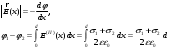 Проверка размерности используемых формул 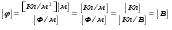 .Тогда подставляем числовые значения  Используя (3) и (4) построим график зависимости 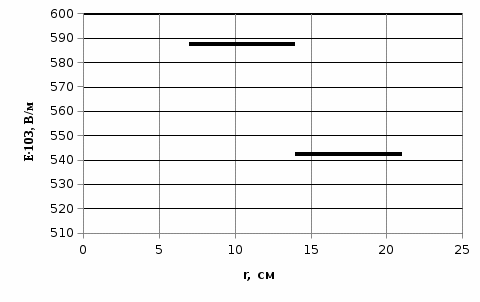для случая, когда  Рис. 1 Зависимость напряженности электрического поля, создаваемого двумя бесконечными плоскостями в воздухе. Анализ РГР 4. В результате выполнения расчетно-графической работы 3: 1. получено соотношение - (3) и (4) - определяющие напряженность электростатического поля между пластинами и вне пластин; 2. рассчитана разность потенциалов между пластинами; 3. построен график изменения напряженности электростатического поля вдоль линии, перпендикулярной пластинам; 4. проведена проверка размерности полученных формул; |
