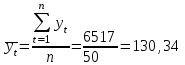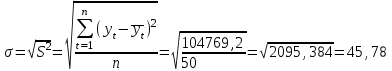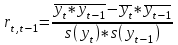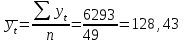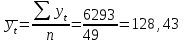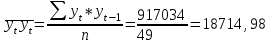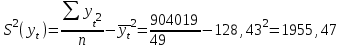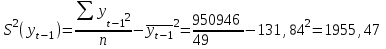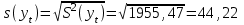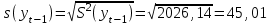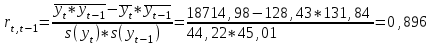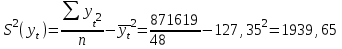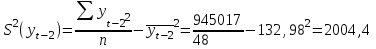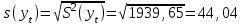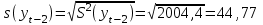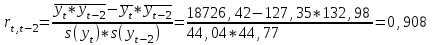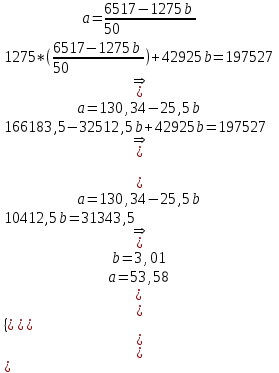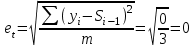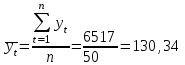
Среднее квадратическое отклонение рассчитаем по формуле:
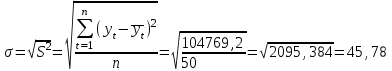
Сдвигаем исходный ряд на 1 уровень. Получаем следующую таблицу:
Yt
|
Yt-1
|
Yt2
|
Yt-12
|
Yt*yt-1
|
57
|
77
|
3249
|
5929
|
4389
|
77
|
75
|
5929
|
5625
|
5775
|
75
|
45
|
5625
|
2025
|
3375
|
45
|
70
|
2025
|
4900
|
3150
|
70
|
73
|
4900
|
5329
|
5110
|
73
|
97
|
5329
|
9409
|
7081
|
97
|
85
|
9409
|
7225
|
8245
|
85
|
63
|
7225
|
3969
|
5355
|
63
|
75
|
3969
|
5625
|
4725
|
75
|
61
|
5625
|
3721
|
4575
|
61
|
110
|
3721
|
12100
|
6710
|
110
|
102
|
12100
|
10404
|
11220
|
102
|
83
|
10404
|
6889
|
8466
|
83
|
103
|
6889
|
10609
|
8549
|
103
|
92
|
10609
|
8464
|
9476
|
92
|
115
|
8464
|
13225
|
10580
|
115
|
93
|
13225
|
8649
|
10695
|
93
|
130
|
8649
|
16900
|
12090
|
130
|
122
|
16900
|
14884
|
15860
|
122
|
111
|
14884
|
12321
|
13542
|
111
|
96
|
12321
|
9216
|
10656
|
96
|
118
|
9216
|
13924
|
11328
|
118
|
98
|
13924
|
9604
|
11564
|
98
|
124
|
9604
|
15376
|
12152
|
124
|
151
|
15376
|
22801
|
18724
|
151
|
146
|
22801
|
21316
|
22046
|
146
|
137
|
21316
|
18769
|
20002
|
137
|
156
|
18769
|
24336
|
21372
|
156
|
134
|
24336
|
17956
|
20904
|
134
|
149
|
17956
|
22201
|
19966
|
149
|
143
|
22201
|
20449
|
21307
|
143
|
176
|
20449
|
30976
|
25168
|
176
|
164
|
30976
|
26896
|
28864
|
164
|
168
|
26896
|
28224
|
27552
|
168
|
154
|
28224
|
23716
|
25872
|
154
|
169
|
23716
|
28561
|
26026
|
169
|
158
|
28561
|
24964
|
26702
|
158
|
142
|
24964
|
20164
|
22436
|
142
|
161
|
20164
|
25921
|
22862
|
161
|
157
|
25921
|
24649
|
25277
|
157
|
186
|
24649
|
34596
|
29202
|
186
|
182
|
34596
|
33124
|
33852
|
182
|
205
|
33124
|
42025
|
37310
|
205
|
193
|
42025
|
37249
|
39565
|
193
|
215
|
37249
|
46225
|
41495
|
215
|
189
|
46225
|
35721
|
40635
|
189
|
203
|
35721
|
41209
|
38367
|
203
|
180
|
41209
|
32400
|
36540
|
180
|
224
|
32400
|
50176
|
40320
|
6293
|
6460
|
904019
|
950946
|
917034
|
Линейный коэффициент автокорреляции rt,t-1 рассчитывается по формуле:
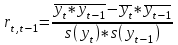
Выборочные средние.
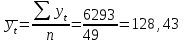

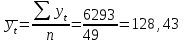
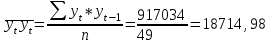
Выборочные дисперсии:
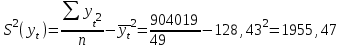
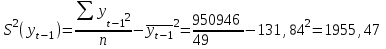
Среднеквадратическое отклонение.
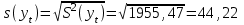
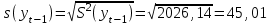
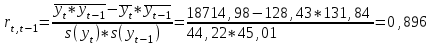
В нашем примере связь между рядами - высокая и прямая.
Частный коэффициент корреляции:
Ф1 = r1=0,896
Сдвигаем исходный ряд на 2 уровней. Получаем следующую таблицу:
Yt
|
Yt-2
|
Yt2
|
Yt-22
|
Yt*yt-2
|
57
|
75
|
3249
|
5625
|
4275
|
77
|
45
|
5929
|
2025
|
3465
|
75
|
70
|
5625
|
4900
|
5250
|
45
|
73
|
2025
|
5329
|
3285
|
70
|
97
|
4900
|
9409
|
6790
|
73
|
85
|
5329
|
7225
|
6205
|
97
|
63
|
9409
|
3969
|
6111
|
85
|
75
|
7225
|
5625
|
6375
|
63
|
61
|
3969
|
3721
|
3843
|
75
|
110
|
5625
|
12100
|
8250
|
61
|
102
|
3721
|
10404
|
6222
|
110
|
83
|
12100
|
6889
|
9130
|
102
|
103
|
10404
|
10609
|
10506
|
83
|
92
|
6889
|
8464
|
7636
|
103
|
115
|
10609
|
13225
|
11845
|
92
|
93
|
8464
|
8649
|
8556
|
115
|
130
|
13225
|
16900
|
14950
|
93
|
122
|
8649
|
14884
|
11346
|
130
|
111
|
16900
|
12321
|
14430
|
122
|
96
|
14884
|
9216
|
11712
|
111
|
118
|
12321
|
13924
|
13098
|
96
|
98
|
9216
|
9604
|
9408
|
118
|
124
|
13924
|
15376
|
14632
|
98
|
151
|
9604
|
22801
|
14798
|
124
|
146
|
15376
|
21316
|
18104
|
151
|
137
|
22801
|
18769
|
20687
|
146
|
156
|
21316
|
24336
|
22776
|
137
|
134
|
18769
|
17956
|
18358
|
156
|
149
|
24336
|
22201
|
23244
|
134
|
143
|
17956
|
20449
|
19162
|
149
|
176
|
22201
|
30976
|
26224
|
143
|
164
|
20449
|
26896
|
23452
|
176
|
168
|
30976
|
28224
|
29568
|
164
|
154
|
26896
|
23716
|
25256
|
168
|
169
|
28224
|
28561
|
28392
|
154
|
158
|
23716
|
24964
|
24332
|
169
|
142
|
28561
|
20164
|
23998
|
158
|
161
|
24964
|
25921
|
25438
|
142
|
157
|
20164
|
24649
|
22294
|
161
|
186
|
25921
|
34596
|
29946
|
157
|
182
|
24649
|
33124
|
28574
|
186
|
205
|
34596
|
42025
|
38130
|
182
|
193
|
33124
|
37249
|
35126
|
205
|
215
|
42025
|
46225
|
44075
|
193
|
189
|
37249
|
35721
|
36477
|
215
|
203
|
46225
|
41209
|
43645
|
189
|
180
|
35721
|
32400
|
34020
|
203
|
224
|
41209
|
50176
|
45472
|
6113
|
6383
|
871619
|
945017
|
898868
|
127,35
|
132,98
|
18158,73
|
19687,85
|
18726,42
|
Выборочные дисперсии:
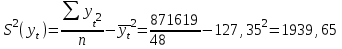
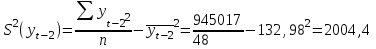
Среднеквадратическое отклонение.
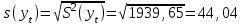
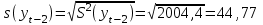
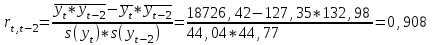
В нашем примере связь между рядами - высокая и прямая.
Уравнение тренда:
Система уравнений МНК:
an + b∑t = ∑y
a∑t + b∑t2 = ∑y*t
Для наших данных система уравнений имеет вид:
50a + 1275b = 6517
1275a + 42925b = 197527
Из первого уравнения выражаем a и подставим во второе уравнение
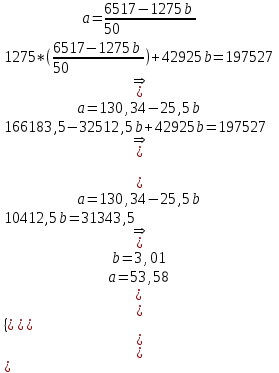
Уравнение тренда:
y = 3.01 t + 53.58
Одним из эмпирических методов является метод скользящей средней.
t
|
y
|
ys
|
Формула
|
(y - ys)2
|
1
|
1
|
-
|
-
|
-
|
2
|
2
|
2
|
(1 + 2 + 3)/3
|
0
|
3
|
3
|
3
|
(2 + 3 + 4)/3
|
0
|
4
|
4
|
4
|
(3 + 4 + 5)/3
|
0
|
5
|
5
|
5
|
(4 + 5 + 6)/3
|
0
|
6
|
6
|
6
|
(5 + 6 + 7)/3
|
0
|
7
|
7
|
7
|
(6 + 7 + 8)/3
|
0
|
8
|
8
|
8
|
(7 + 8 + 9)/3
|
0
|
9
|
9
|
9
|
(8 + 9 + 10)/3
|
0
|
10
|
10
|
10
|
(9 + 10 + 11)/3
|
0
|
11
|
11
|
11
|
(10 + 11 + 12)/3
|
0
|
12
|
12
|
12
|
(11 + 12 + 13)/3
|
0
|
13
|
13
|
13
|
(12 + 13 + 14)/3
|
0
|
14
|
14
|
14
|
(13 + 14 + 15)/3
|
0
|
15
|
15
|
15
|
(14 + 15 + 16)/3
|
0
|
16
|
16
|
16
|
(15 + 16 + 17)/3
|
0
|
17
|
17
|
17
|
(16 + 17 + 18)/3
|
0
|
18
|
18
|
18
|
(17 + 18 + 19)/3
|
0
|
19
|
19
|
19
|
(18 + 19 + 20)/3
|
0
|
20
|
20
|
20
|
(19 + 20 + 21)/3
|
0
|
21
|
21
|
21
|
(20 + 21 + 22)/3
|
0
|
22
|
22
|
22
|
(21 + 22 + 23)/3
|
0
|
23
|
23
|
23
|
(22 + 23 + 24)/3
|
0
|
24
|
24
|
24
|
(23 + 24 + 25)/3
|
0
|
25
|
25
|
25
|
(24 + 25 + 26)/3
|
0
|
26
|
26
|
26
|
(25 + 26 + 27)/3
|
0
|
27
|
27
|
27
|
(26 + 27 + 28)/3
|
0
|
28
|
28
|
28
|
(27 + 28 + 29)/3
|
0
|
29
|
29
|
29
|
(28 + 29 + 30)/3
|
0
|
30
|
30
|
30
|
(29 + 30 + 31)/3
|
0
|
31
|
31
|
31
|
(30 + 31 + 32)/3
|
0
|
32
|
32
|
32
|
(31 + 32 + 33)/3
|
0
|
33
|
33
|
33
|
(32 + 33 + 34)/3
|
0
|
34
|
34
|
34
|
(33 + 34 + 35)/3
|
0
|
35
|
35
|
35
|
(34 + 35 + 36)/3
|
0
|
36
|
36
|
36
|
(35 + 36 + 37)/3
|
0
|
37
|
37
|
37
|
(36 + 37 + 38)/3
|
0
|
38
|
38
|
38
|
(37 + 38 + 39)/3
|
0
|
39
|
39
|
39
|
(38 + 39 + 40)/3
|
0
|
40
|
40
|
40
|
(39 + 40 + 41)/3
|
0
|
41
|
41
|
41
|
(40 + 41 + 42)/3
|
0
|
42
|
42
|
42
|
(41 + 42 + 43)/3
|
0
|
43
|
43
|
43
|
(42 + 43 + 44)/3
|
0
|
44
|
44
|
44
|
(43 + 44 + 45)/3
|
0
|
45
|
45
|
45
|
(44 + 45 + 46)/3
|
0
|
46
|
46
|
46
|
(45 + 46 + 47)/3
|
0
|
47
|
47
|
47
|
(46 + 47 + 48)/3
|
0
|
48
|
48
|
48
|
(47 + 48 + 49)/3
|
0
|
49
|
49
|
49
|
(48 + 49 + 50)/3
|
0
|
50
|
50
|
-
|
-
|
-
|
Стандартная ошибка (погрешность) рассчитывается по формуле:
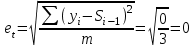
|
 Скачать 267.33 Kb.
Скачать 267.33 Kb.