ДЗ - Контрольная работа математика. Задача 1 1 Задача 2 7 Задача 3 11 Задача 4 22 Задача 5 25 Список использованных источников 31 Задача 1
 Скачать 267.33 Kb. Скачать 267.33 Kb.
|
Задача 4Пусть U={u1, u2, u3, u4, u5, u6, u7}, 𝑋 = {(𝑥; μx(𝑥))}, 𝑌 = {(𝑦; μy(𝑦))}, 𝑥, 𝑦 ∈ 𝑈
Представить множества 𝑋 и 𝑌 геометрически. Найти функции принадлежности множеств 𝑋̅, 𝑌̅, 𝑋 ∪ 𝑌, 𝑋 ∩ 𝑌, 𝑋⨁𝑌. Найти абсолютное и относительное евклидово расстояния между множествами 𝑋 и 𝑌 и расстояние по Хеммингу. Найти обычные множества 𝑋0 и 𝑌0, ближайшие к 𝑋 и 𝑌 соответственно. Вычислить для каждого множества индексы нечеткости. Решение: Запишем данное нечеткое множество в виде: 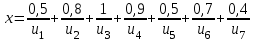 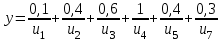 Множества можно изобразить графически, рисунок 3. 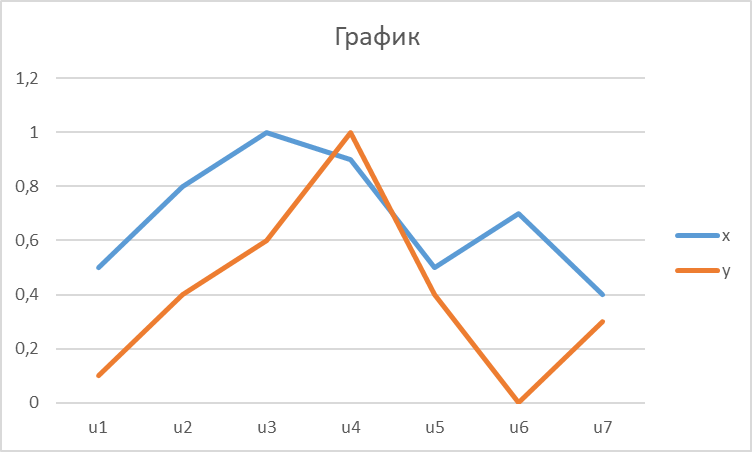 Рисунок 3 - График Найдем следующие множества и функции принадлежности для них: 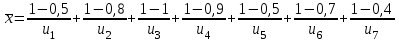 = =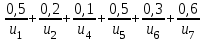 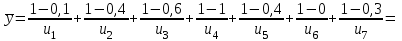 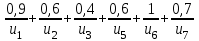 Представим в табличном виде:
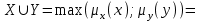 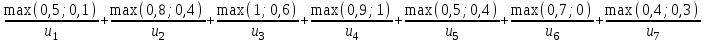 = =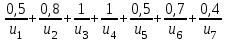 Представим в табличном виде:
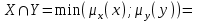 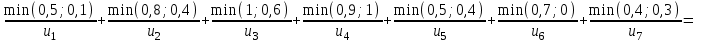 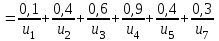 Представим в табличном виде:
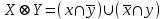 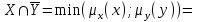 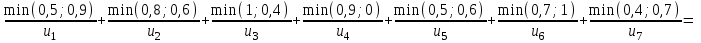 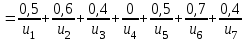 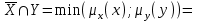 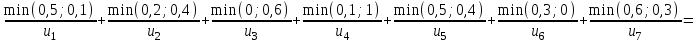 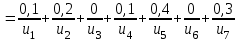 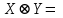 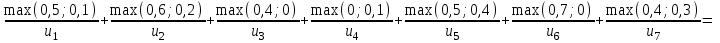 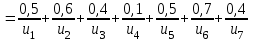 Представим в табличном виде:
Абсолютное евклидово расстояние 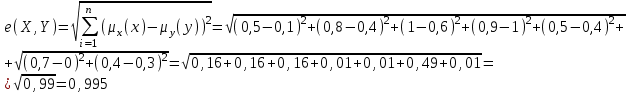 Относительное евклидово расстояние 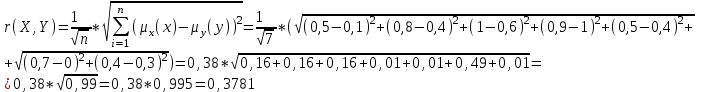 Расстояние по Хеммингу: 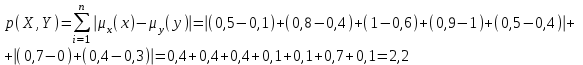 Для нахождения обычных множеств, нужно сравнить значения характеристической функции с 0,5. Если больше, то 1, и если меньше, то 0.
Индекс нечеткости по Хеммингу: 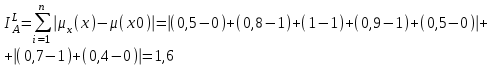 Линейные индексы: 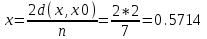 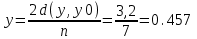 |

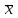 )
)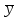 )
)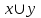 )
)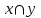 )
)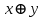 )
)