Задания контрольных работ гиму. Задача 1 3 Задача 2 6 Задача 3 7 Задача 4 10 Задача 5 11 Задача 6 13 Список литературы 15

• Название: Задача 1 3 Задача 2 6 Задача 3 7 Задача 4 10 Задача 5 11 Задача 6 13 Список литературы 15
• Дата: 26.04.2023
• Размер: 77.75 Kb.
• Имя файла: Задания контрольных работ гиму.docx
• Тип: Задача; #1092307

Вариант 5

Оглавление

Задача 5.1 3

Задача 5.2 6

Задача 5.3 7

Задача 5.4 10

Задача 5.5 11

Задача 5.6 13

Список литературы 15

Задача 5.1

За отчетный период деятельность группы предприятий характеризуется следующими данными на основании статистического и финансового учета:

№ п/п	Валовая продукция, млн. руб.	Среднесписочное число работающих, чел.	Среднегодовая стоимость основных производственных фондов, млн. руб.	Прибыль, тыс. руб.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16	367 473 982 228 1337 483 782 758 967 927 342 1298 1557 123 842 1358	152 217 521 130 345 231 346 204 409 488 203 528 362 133 400 332	397 468 1592 438 1247 673 762 588 907 1173 742 478 957 173 532 948	30 44 78 45 95 25 60 72 90 60 32 91 116 24 63 86

По данным таблицы произвести группировку предприятий по размеру основных фондов, выделив 4 группы (60%). Установить зависимость прибыли предприятия от численности работников, стоимости основных фондов и объема выпускаемой продукции (30%). Сделать выводы (10%).
Решение:

1. Величина интервала (h) при равных интервалах группировки определяется по формуле: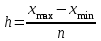

,

где х_max и x_min - максимальное и минимальное значение данного признака;

n – число групп.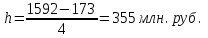


2. Составим рабочую таблицу (табл. 5.1.1):
Таблица 5.1.1 Рабочая таблица

Группы предприятий по размеру ОПФ, млн.руб.	№ п/п	Среднегодовая стоимость ОПФ, млн. руб.	Валовая продукция, млн. руб.	Среднесписочное число работающих, чел.	Прибыль, тыс. руб.
173-532	14	173	123	133	24
	1	397	367	152	30
	4	438	228	130	45
	2	468	473	217	44
	12	478	1298	528	91
Итого	5	1954	2489	1160	234
532-887	15	532	842	400	63
	8	588	758	204	72
	6	673	483	231	25
	11	742	342	203	32
	7	762	782	346	60
Итого	5	3297	3207	1384	252
887-1242	9	907	967	409	90
	16	948	1358	332	86
	13	957	1557	362	116
	10	1173	927	488	60
Итого	4	3985	4809	1591	352
1242-1597	5	1247	1337	345	95
	3	1592	982	521	78
Итого	2	2839	2319	866	173
Всего	16	12075	12824	5001	1011

На основании табл. 5.1.1 строим табл. 5.1.2:

Таблица 5.1.2 Аналитическая группировка предприятий по среднегодовой стоимости ОПФ

Группы предприятий по стоимости ОПФ, млн.руб.	Число предприятий	Валовая продукция, млн. руб.		Среднесписочное число работающих, чел.		Прибыль, тыс. руб.
		всего	в среднем на 1 предприятие	всего	в среднем на 1 предприятие	всего	в среднем на 1 предприятие
173-532	5	2489	497,8	1160	232,0	234	46,8
532-887	5	3207	641,4	1384	276,8	252	50,4
887-1242	4	4809	1202,3	1591	397,8	352	88,0
1242-1597	2	2319	1159,5	866	433,0	173	86,5
Итого	16	12824	801,5	5001	312,6	1011	63,2

Результаты проведенной аналитической группировки предприятий по средней стоимости ОПФ показывает, что распределение предприятий является неравномерным: преобладают предприятия, стоимость ОПФ которых составляет 173-532 млн.руб. и532-887 млн.руб. В каждую из указанных групп входит по 5 предприятий, доля которых составляет 31,3% в общей численности предприятий. Наименее распространена стоимость более 1242 млн.руб., что характерно для двух предприятий (или 12,5%).

Среднегодовая стоимость большей части предприятий (14 ед.) составляет менее 1242 млн.руб.

Отметим, что с ростом средней стоимости ОПФ увеличивается и средняя прибыль. Т.е. между стоимостью ОПФ и суммой прибыли имеется положительная зависимость, однако указанная тенденция не является строгой, т.к. всегда рост стоимости ОПФ сопровождается ростом прибыли. Т.е. чем больше размер предприятия, тем больше сумма прибыли.

Между суммой прибыли и валовой продукции, а также между прибылью и среднесписочным числом работающих наблюдается нестрогая положительная зависимость.

Задача 5.2

Имеются данные о дальности перевозок и грузообороте 5 грузовых автомашин за день. Определить среднюю дальность перевозки 1 тонны груза (80%).

№ автомобиля	Дальность перевозки 1 тонны груза, км	Грузооборот, т/км
1 2 3 4 5	14 7 17 10 16	68 43 58 133 63

Обоснуйте правильность выбора формулы для расчета (20%).
Решение:

Логическая формула расчета дальности перевозки грузов следующая: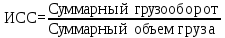



В данном случае известен числитель ИСС, а знаменатель находится как частное от деления грузооборота и дальности перевозки 1 тонны груза, т.е. это формула средней гармонической взвешенной: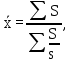



где s - дальность перевозки 1 тонны груза;

S – грузооборот.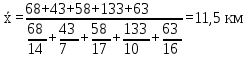

В среднем дальность перевозки 1 тонны груза составляет 11,5 км.

Задача 5.3

В целях контроля за соблюдением норм расхода сырья проведено выборочное обследование партии готовой продукции. При механическом способе отбора 2% изделий получены следующие данные о весе обследованных единиц:

Вес изделия, г	Число образцов, шт.
До 2000	13
от 2001 до 2050	22
от 2051 до 2100	67
от 2101 до 2150	12
свыше 2150	11
Итого	125

При условии, что к стандартной продукции относятся изделия с весом от 2001 до 2100 г, установите для всей партии:

1) с вероятностью 0,95 возможные пределы удельного веса стандартной продукции (50%);

2) с вероятность 0,997 возможные пределы среднего веса одного изделия в генеральной совокупности (50%).
Решение:

1) Рассчитаем долю стандартной продукции во всей партии: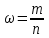

,

где m – число стандартной продукции во всей партии.

n – объем выборки.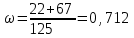


Предельная ошибка доли: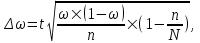



_{где t- коэффициент доверия (Р=0,95t=1,96);}

N – число единиц в генеральной совокупности.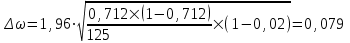



Доверительные пределы генеральной доли: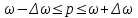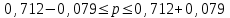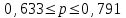







С вероятностью 95% можно утверждать, что в генеральной совокупности доля стандартной продукции может составить от 63,3% до 79,1%.

2. Определим средний вес одного изделия по формуле средней арифметической взвешенной: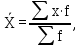



где х - середина интервала;

f - число образцов.
Таблица 5.3.1 – Расчетная таблица

Вес изделия, г	Середина интервала, Х	Число образцов, f	Х∙f
от 1951 до 2000	(1951+2000):2=1975,5	13	25681,5	8911	115848
от 2001 до 2050	2025,5	22	44561,0	1971	43370
от 2051 до 2100	2075,5	67	139058,5	31	2101
от 2101 до 2150	2125,5	12	25506,0	3091	37096
от 2151 до 2200	2175,5	11	23930,5	11151	122665
Итого		125	258737,5		321080

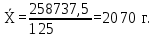В среднем вес одного изделия составляет 2070 г.

Рассчитаем дисперсию по формуле: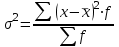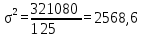





Предельная ошибка выборочной средней: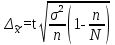

,

При Р=0,997 t=3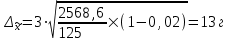


_{Границы генеральной средней:}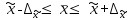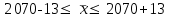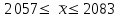







С вероятностью 99,7% можно утверждать, что для генеральной совокупности изделий средний вес одного изделия составит не менее 2057 г и не более 2083 г.

Задача 5.4

Имеются следующие данные о распределении строительных бригад области по производительности труда и себестоимости единицы продукции:

Себестоимость	Производительность			Итого
	высокая	средняя	низкая
Высокая	16	15	35		66
Средняя	23	34	24		81
Низкая	42	12	12		66
Итого	81	61	71		213

Рассчитайте коэффициент взаимной сопряженности Пирсона (80%). Сделайте вывод (20%).
Решение:

Рассчитаем коэффициент взаимной сопряженности Пирсона по формуле: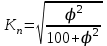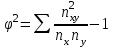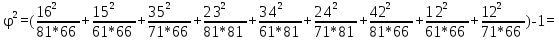






=0,176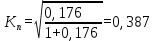


Коэффициент взаимной сопряженности Пирсона должен быть не меньше 0,5. Связь между себестоимостью и производительностью не подтверждается.

Задача 5.5

Имеются следующие данные о товарных запасах торгового предприятия (тыс. руб., сопоставимые данные):

Годы	На 1.01	На 1.04	На 1.07	На 1.10
2014	75	72	73	74
2015	70	73	86	85
2016	73	84	95	78
2017	98	-	-	-

Определите абсолютное (40%) и относительное (40%) изменение средней суммы товарных запасов в 2017 г. по сравнению с 2014, 2015 и 2016 гг. Интерпретируйте полученные результаты (20%).
Решение:

Рассчитаем среднюю сумму товарных запасов по формуле средней хронологической простой: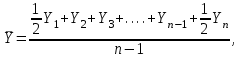



где Y₁ – начальный уровень ряда;

Y_n ^– последний уровень ряда;

n - число уровней ряда.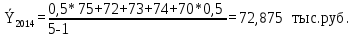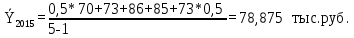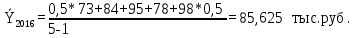






В 2016 г. величина средних товарных запасов составила 85,625 ытс.руб.

2. Абсолютный прирост: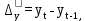



где y_t,t-1 – значение показателя в периоде t и t-1.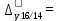
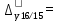85,625-72,875=+12,75 тыс.руб.

85,625-78,875=+6,75 тыс.руб.
Темп роста: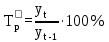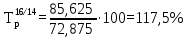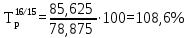





Результаты проведенных расчетов показывают, что в 2016 г. товарные запасы повышались. В целом за исследуемый период запасы увеличились на 12,75 тыс.руб. или на 17,5%.

Задача 5.6

Имеются данные о себестоимости и объеме продукции предприятия.

Определите:

1) агрегатный индекс себестоимости продукции (по модели Пааше) (30%);

2) агрегатный индекс физического объема продукции (по модели Ласпейреса) (30%);

3) общий индекс затрат на производство (30%).

Изделия	Себестоимость единицы, ден.ед.		Выработано продукции, ед.
	базисный период	отчетный период		базисный период	отчетный период
А	133	143		1200	1100
Б	92	82		3600	4200
В	107	115		5200	4700

Покажите взаимосвязь между индексами (10%).
Решение:

1) Рассчитаем агрегатный индекс себестоимости продукции по формуле: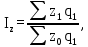



где z_0,1 – себестоимость единицы продукции в базисном и отчетном периодах соответственно.

q₁ – физический объем производства отчетного периода.
Сводим расчеты в табл. 5.6.1:
Таблица 5.6.1 - Расчетная таблица

Изделия	z0	z1	q0	q1	z0q0	z0q1	z1q1
А	133	143	1200	1100	159600	146300	157300
Б	92	82	3600	4200	331200	386400	344400
В	107	115	5200	4700	556400	502900	540500
Итого					1047200	1035600	1042200

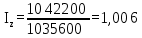В отчетном периоде по сравнению с базисным в целом по продукции себестоимость продукции увеличилась на 0,68%.

2) Агрегатный индекс физического объема продукции: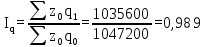



В отчетном периоде по сравнению с базисным в целом по продукции физический объем производства продукции уменьшился на 1,1% (98,9-100).

3) Общий индекс затрат на производство продукции: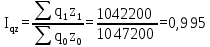



В отчетном периоде по сравнению с базисным в целом по продукции сумма затрат на производство продукции снизилась на 0,5% (99,5-100).

Покажем взаимосвязь между индексами: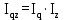

=0,989*1,006=0,995

Список литературы

1. 
   Батуева А.Д., Хохлова О.А.. Макроэкономическая статистика: Учебное пособие, Улан-Удэ, ВСГТУ, 2018.- 140с.
   
2. 
   Хохлова О.А.. Антохонова И.В. Социально-экономическая статистика (курс лекций). Учебное пособие: - Улан-Удэ.: Изд-во БГСХА, 2019. -187с.
   
3. 
   Курс социально-экономической статистики: Учебник /Под. ред. М.Г. Назарова. - М.: Финстатинформ, ЮНИТИ-ДАНА, 2020. –771с.
   
4. 
   Общая теория статистики: Учебник /А.И.Харченко, О.Э.Башина, В.Т.Бабурин и др.; Под ред. А.А.Спирина, О.Э.Башиной. – М.: Финансы и статистика, 2020. – 296с.
   
5. 
   Статистика: Курс лекций /Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др./ Под ред. В.Г.Ионина. – Новосибирск.: Изд-во НГАЭиУ - М.: ИНФРА-М, 2018. – 310с.