Задачи линейного программирования. _Готовое 84-04-3. Задача 1 3 Задача 2 6 Задача 3 9 Задача 4 15
 Скачать 109.17 Kb. Скачать 109.17 Kb.
|
|
[Титульный лист] Оглавление Задача 1 3 Задача 2 6 Задача 3 9 Задача 4 15 Задача 1На сортировочную станцию прибывают составы с интенсивностью 0,9 состава в час. Среднее время обслуживания одного состава 0,7 часа. Определить показатели эффективности работы сортировочной станции: интенсивность потока обслуживаний, среднее число заявок в очереди, интенсивность нагрузки канала (трафик), вероятность, что канал свободен, вероятность, что канал занят, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе (табл. 4.2). Таблица 4.2 Исходные данные для решения задачи 1
Решение. Сортировочную станцию можно рассматривать как одноканальную СМО с неограниченным ожиданием (т. е. с очередью). Таким образом, параметры системы: число каналов n = 1, число мест в очереди m = 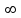 . .Интенсивность входящего потока λ = 0,4 состава в час, среднее время обслуживания одной заявки 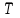 об = 0,6 ч, интенсивность потока обслуживаний об = 0,6 ч, интенсивность потока обслуживаний 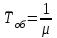 , (4.1) , (4.1)μ = 1/0,6 = 1,67. Таким образом, нагрузка системы 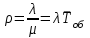 , (4.2) , (4.2)ρ = 0,4/1,67 = 0,24, или ρ = 0,4 ∙ 0,6 = 0,24. Среднее число составов, ожидающих обслуживания,  , (4.3) , (4.3)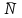 оч = 0,242/(1 – 0,24) = 0,076. оч = 0,242/(1 – 0,24) = 0,076.Так как ρ < 1, то очередь составов на сортировку не может бесконечно возрастать, значит, предельные вероятности существуют. Вероятность того, что станция свободнаp0, рассчитывается по следующей формуле: pk = ρk(1 – ρ); k = 0,1,2… p0 =1 – ρ.(4.4) p0 = 1 – 0,24 = 0,76, тогда вероятность того, что станция занята pзан = 1 – 0,76 = 0,24. Среднее число заявок (составов) в системе (на сортировочной станции) рассчитывается по следующей формуле: 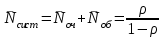 , (4.5) , (4.5)где 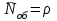 ; ; 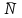 сист = 0,24/(1 – 0,24) = 0,316 или сист = 0,24/(1 – 0,24) = 0,316 или 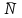 сист = 0,24 + 0,316 = 0,56. сист = 0,24 + 0,316 = 0,56.Среднее время пребывания заявки (состава) в очереди (в ожидании сортировки) 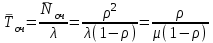 , (4.6) , (4.6)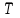 оч = 0,076/0,4 = 0,242/(0,4(1 – 0,24)) = 0,24/(1,67(1 – 0,24)) = 0,19. оч = 0,076/0,4 = 0,242/(0,4(1 – 0,24)) = 0,24/(1,67(1 – 0,24)) = 0,19.Среднее время пребывания заявки (состава) в системе (на сортировочной горке под обслуживанием в ожидании обслуживания) 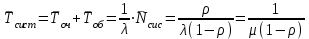 , (4.7) , (4.7)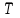 сист = 0,6 + 0,19 = 0,24/(0,4(1 – 0,24)) = 0,316/0,4 = 1/(1,67(1 – 0,24)) = 0,79. сист = 0,6 + 0,19 = 0,24/(0,4(1 – 0,24)) = 0,316/0,4 = 1/(1,67(1 – 0,24)) = 0,79.Вывод. Очевидно, что скорость обслуживания составов на сортировочной станции высокая, так как время на обслуживание (0,6 ч) превышает время на ожидание обслуживания (0,19 ч). | |||||||||||||||||||||||||||||||||||||||||||
