Задачи линейного программирования. _Готовое 84-04-3. Задача 1 3 Задача 2 6 Задача 3 9 Задача 4 15
 Скачать 109.17 Kb. Скачать 109.17 Kb.
|
Задача 4На три базы А1, А2, А3 производиться поставка однородного груза в количестве: 220 тонн на базу А1; 180 тонн на базу А2; 200 тонн на базу А3. Полученный груз требуется перевезти в пять пунктов в количестве: 60 тонн в пункт 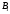 ; 180 тонн в пункт ; 180 тонн в пункт 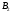 ; 160 тонн в пункт ; 160 тонн в пункт 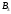 ; 50 тонн в пункт ; 50 тонн в пункт 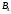 ; 150 тонн в пункт ; 150 тонн в пункт 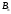 . Составьте оптимальный план перевозок. Стоимость перевозки груза в соответствующий пункт приведена в матрице C: . Составьте оптимальный план перевозок. Стоимость перевозки груза в соответствующий пункт приведена в матрице C: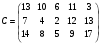 . . Решение: По условию задачи составим матрицу перевозок.
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 220 + 180 + 200 = 600 ∑b = 60 + 180 + 160 + 50 + 150 = 600 Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. Занесем исходные данные в распределительную таблицу.
Этап I. Поиск первого опорного плана. 1. Используя метод «минимального элемента», построим первый опорный план транспортной задачи. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел ai, или bj. Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены. Искомый элемент равен c23=2. Для этого элемента запасы равны 180, потребности 160. Поскольку минимальным является 160, то вычитаем его. x23 = min(180,160) = 160.
Искомый элемент равен c15=3. Для этого элемента запасы равны 220, потребности 150. Поскольку минимальным является 150, то вычитаем его. x15 = min(220,150) = 150.
Искомый элемент равен c22=4. Для этого элемента запасы равны 20, потребности 180. Поскольку минимальным является 20, то вычитаем его. x22 = min(20,180) = 20.
Искомый элемент равен c32=8. Для этого элемента запасы равны 200, потребности 160. Поскольку минимальным является 160, то вычитаем его. x32 = min(200,160) = 160.
Искомый элемент равен c34=9. Для этого элемента запасы равны 40, потребности 50. Поскольку минимальным является 40, то вычитаем его. x34 = min(40,50) = 40.
Искомый элемент равен c14=11. Для этого элемента запасы равны 70, потребности 10. Поскольку минимальным является 10, то вычитаем его. x14 = min(70,10) = 10.
Искомый элемент равен c11=13. Для этого элемента запасы равны 60, потребности 60. Поскольку минимальным является 60, то вычитаем его. x11 = min(60,60) = 60.
В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность пунктов удовлетворена, а план соответствует системе ограничений транспортной задачи. 2. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n - 1 = 7. Следовательно, опорный план является невырожденным. Значение целевой функции для этого опорного плана равно: F(x) = 13*60 + 11*10 + 3*150 + 4*20 + 2*160 + 8*160 + 9*40 = 3380 ус. ед. |
