Задачи линейного программирования. _Готовое 84-04-3. Задача 1 3 Задача 2 6 Задача 3 9 Задача 4 15
 Скачать 109.17 Kb. Скачать 109.17 Kb.
|
Задача 2Интенсивность потока пассажиров в кассах железнодорожного вокзала составляет λ = 1,42 чел. в мин. Средняя продолжительность обслуживания кассиром одного пассажира 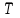 об = 1 мин. Определить минимальное количество кассиров n = nmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n = nmin (вероятность того, что в узле расчета отсутствуют покупатели, вероятность очереди, среднее число заявок находящихся в очереди, среднее время пребывания заявки в очереди, среднее число заявок, находящихся в системе, среднее время пребывания заявки в системе, доля занятых обслуживанием кассиров, абсолютная пропускную способность) (табл. 4.3). об = 1 мин. Определить минимальное количество кассиров n = nmin, при котором очередь не будет расти до бесконечности, и соответствующие характеристики обслуживания при n = nmin (вероятность того, что в узле расчета отсутствуют покупатели, вероятность очереди, среднее число заявок находящихся в очереди, среднее время пребывания заявки в очереди, среднее число заявок, находящихся в системе, среднее время пребывания заявки в системе, доля занятых обслуживанием кассиров, абсолютная пропускную способность) (табл. 4.3).Таблица 4.3 Исходные данные для решения задачи 2
Указание. Прежде чем использовать формулы предельных вероятностей, необходимо быть уверенным в их существовании, ведь в случае, когда время t →  , очередь может неограниченно возрастать. Доказано, что если ρ < 1, т. е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ ≥ 1, очередь растет до бесконечности. Очередь не будет возрастать до бесконечности при условии ρ / n < 1, т. е. при n > ρ. , очередь может неограниченно возрастать. Доказано, что если ρ < 1, т. е. среднее число приходящих заявок меньше среднего числа обслуженных заявок (в единицу времени), то предельные вероятности существуют. Если ρ ≥ 1, очередь растет до бесконечности. Очередь не будет возрастать до бесконечности при условии ρ / n < 1, т. е. при n > ρ.Решение. n > 1, m =  , т. е. имеем многоканальную систему с неограниченной очередью. По условию λ = 1,42 (1/мин). Показатель нагрузки системы определяется по формуле (4.2): ρ = 1,42∙1 = 1,42. , т. е. имеем многоканальную систему с неограниченной очередью. По условию λ = 1,42 (1/мин). Показатель нагрузки системы определяется по формуле (4.2): ρ = 1,42∙1 = 1,42. Очередь не будет возрастать до бесконечности при условии ρ / n < 1, т. е. при n > ρ = 1,42. Таким образом, минимальное количество контролеров-кассиров nmin = 2. Найдем характеристики обслуживания СМО при nmin = 2. Вероятность того, что в узле расчета отсутствуют покупатели, определяется по формуле 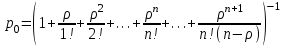 , (4.8) , (4.8)р0 = (1 + 1,42 + 1,422/2! + 1,423/(3!(3 – 1,42)))–1 = 0,061, т.е. в среднем 6,1% времени контролеры-кассиры будут простаивать. Вероятность того, что в узле расчета будет очередь, определяется по формуле 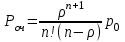 , (4.9) , (4.9)Роч = 1,423/(2!(2 – 1,42)) ∙ 0,061 = 0,625. Среднее число покупателей, находящихся в очереди, определяется по формуле: 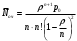 , (4.10) , (4.10)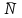 оч = 0,061 ∙ 1,423/(2 ∙ 2!(1 – 1,42/2)2) = 3,715. оч = 0,061 ∙ 1,423/(2 ∙ 2!(1 – 1,42/2)2) = 3,715. Среднее время ожидания в очереди определяется по формуле: 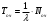 , (4.11) , (4.11)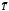 оч = 3,715/1,42 = 2,616 мин. оч = 3,715/1,42 = 2,616 мин.Среднее число покупателей в узле расчета определяется по формуле 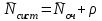 , (4.12) , (4.12)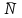 сист = 2,616 + 1,42 = 5,136. сист = 2,616 + 1,42 = 5,136.Среднее время нахождения покупателей в узле расчета определяется по формуле: 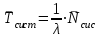 , (4.13) , (4.13)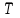 сист = 5,136/1,42 = 3,62 мин. сист = 5,136/1,42 = 3,62 мин.Среднее число контролеров-кассиров, занятых обслуживанием покупателей, определяется по формуле: 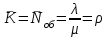 , (4.14) , (4.14)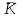 = 1,42. = 1,42.Коэффициент (доля) занятых обслуживанием контролеров-кассиров: 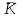 = ρ/n = 1,42/2 = 0,71. = ρ/n = 1,42/2 = 0,71.Абсолютная пропускная способность узла расчета А = 1,42 (1/мин), или 85,2 (1/ч), т. е. 85,2 покупателей в час. Вывод. Анализ характеристик обслуживания свидетельствует о значительной перегрузке узла расчета при наличии двух кассиров. | |||||||||||||||||||||||||||||||||||||||||||
