высшая математика. черновой. Задача 1 Элементы линейной алгебры, векторной алгебры и аналитической геометрии (
 Скачать 111.62 Kb. Скачать 111.62 Kb.
|
|
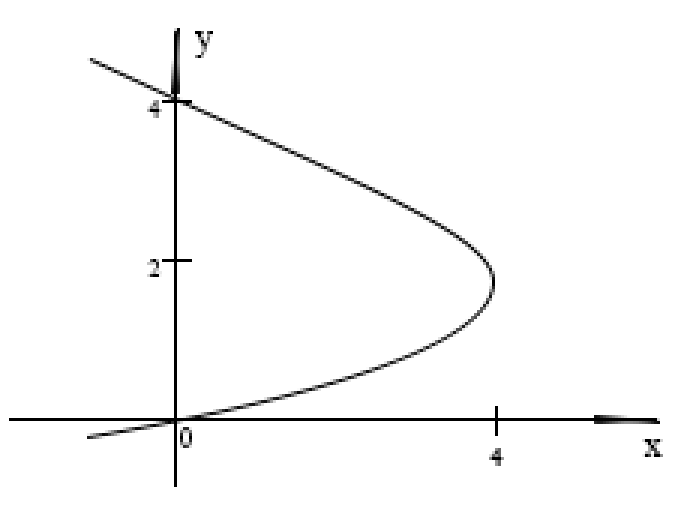
Курдесова Е.В ФЗО Задача 1 Элементы линейной алгебры, векторной алгебры и аналитической геометрии (Вариант 9 ) Записать систему линейных уравнений в матричной форме и решить методом Крамера 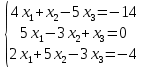  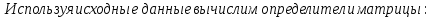 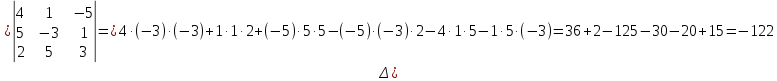 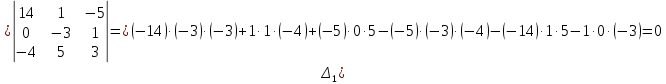 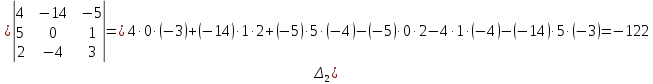 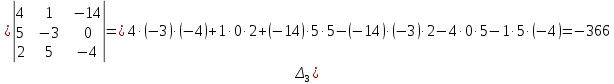 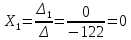 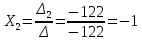 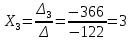 Задача 2 (59) Найти производные 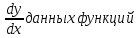 : :А) 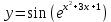 Б) 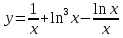 В) 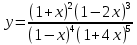 Г) 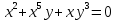 Решение: a) 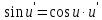 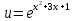 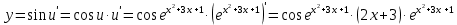 б) 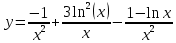 в) 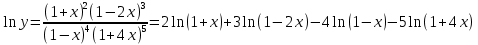 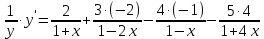 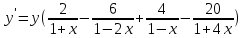 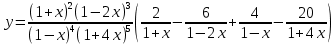 г) 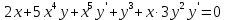 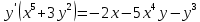 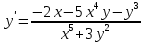 Задача 3 (89) Найти наибольшее и наименьшее значения функции y = f (x) на отрезке [a; b]. 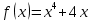 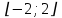 1. Находим и приравниваем к нулю производную 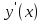 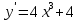 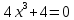 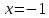 2. Находим критические точки, принадлежащие интервалу 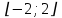 Интервалу 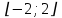 принадлежит только точка принадлежит только точка  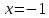 3. Вычисляем значения функции в критической точке и на концах отрезка 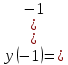 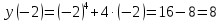 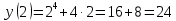 4. Из найденных значений выбираем наибольшее и наименьшее 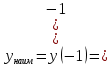 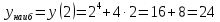 Задача 4 (99) Вычислить неопределенные интегралы: а) методом замены переменной; б) методом интегрирования по частям. a) 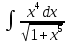 ; ;б) 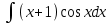 Решение: А)  Производим замену: Производим замену: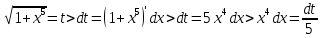 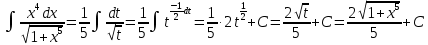 , где С=const , где С=constБ) Формула интегрирования по частям 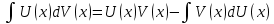 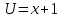 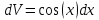 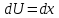 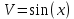 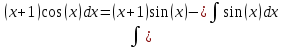 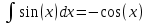 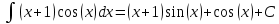 Задача 5 (119) Вычислить неопределенные интегралы от иррациональных и от тригонометрических функций. А) 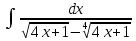 Б) 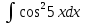 Решение: А) 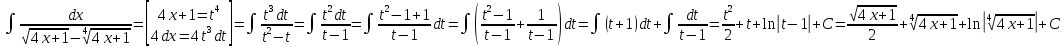 Б) 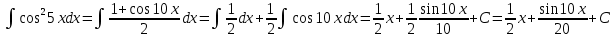 Задача 6 (129) Вычислить площадь фигуры, ограниченной данными линиями, и изобразить фигуру на чертеже. xy=4 x=4 y=4 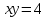 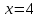 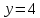 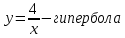 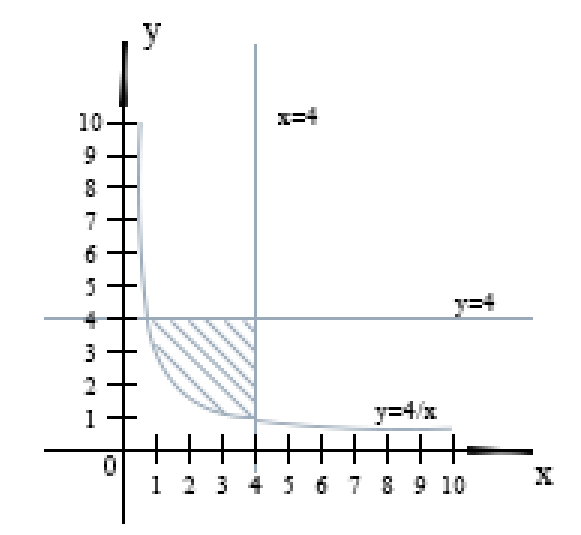 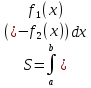 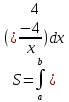  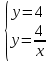 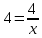 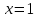 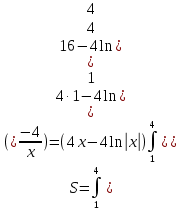 Задача 7 (159) Найти общее решение дифференциальных уравнений первого порядка. 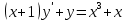 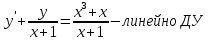 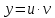 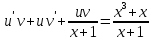 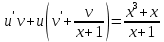 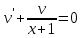 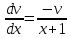 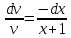 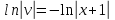 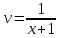 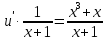 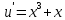 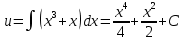 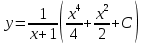 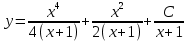 Задача 8 (179) Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям. 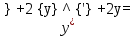 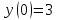 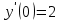 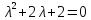 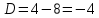 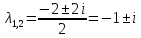 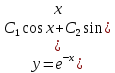 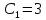 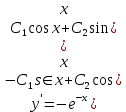 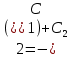 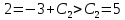 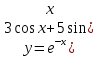 Задача 9 (189) Найти общее решение линейного дифференциального уравнения второго порядка 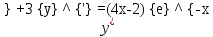 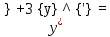 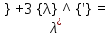 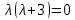 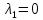 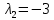 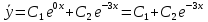  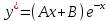 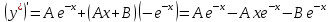 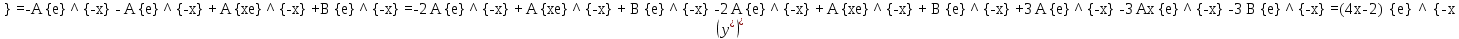 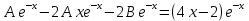 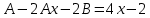 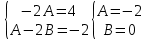 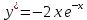 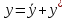 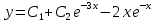 Задача 10 (79) Исследовать функцию y = f (x) и построить ее график. 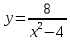 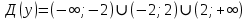 Асимптоты: 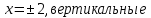 Т.к 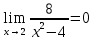 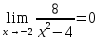 Наклонные асимптоты: 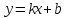 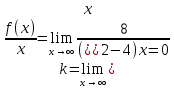 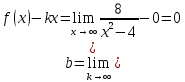 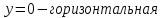 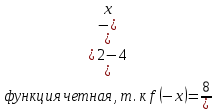  COx: 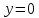 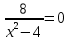 COy: 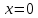 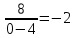 A(0;-2) Интервалы возрастающей, убывающей, точки экст. 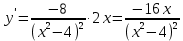 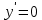 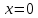 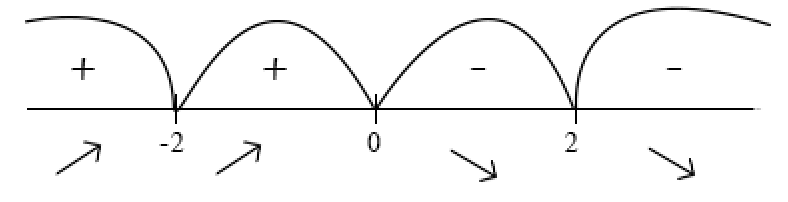 т.max A(0;-2) -т.max Интервалы выпуклости, вогнутости 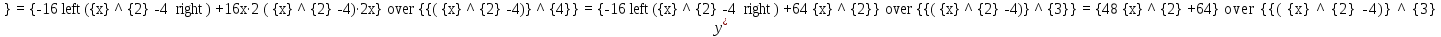 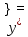 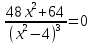 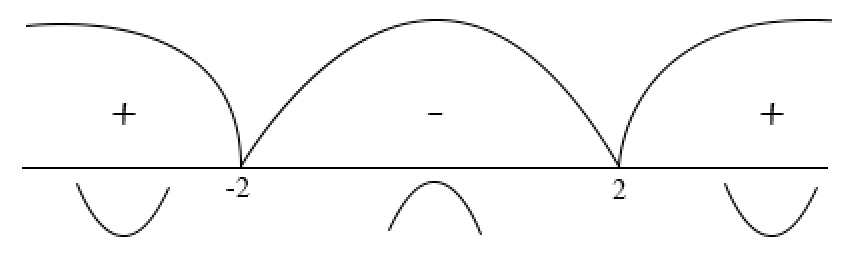 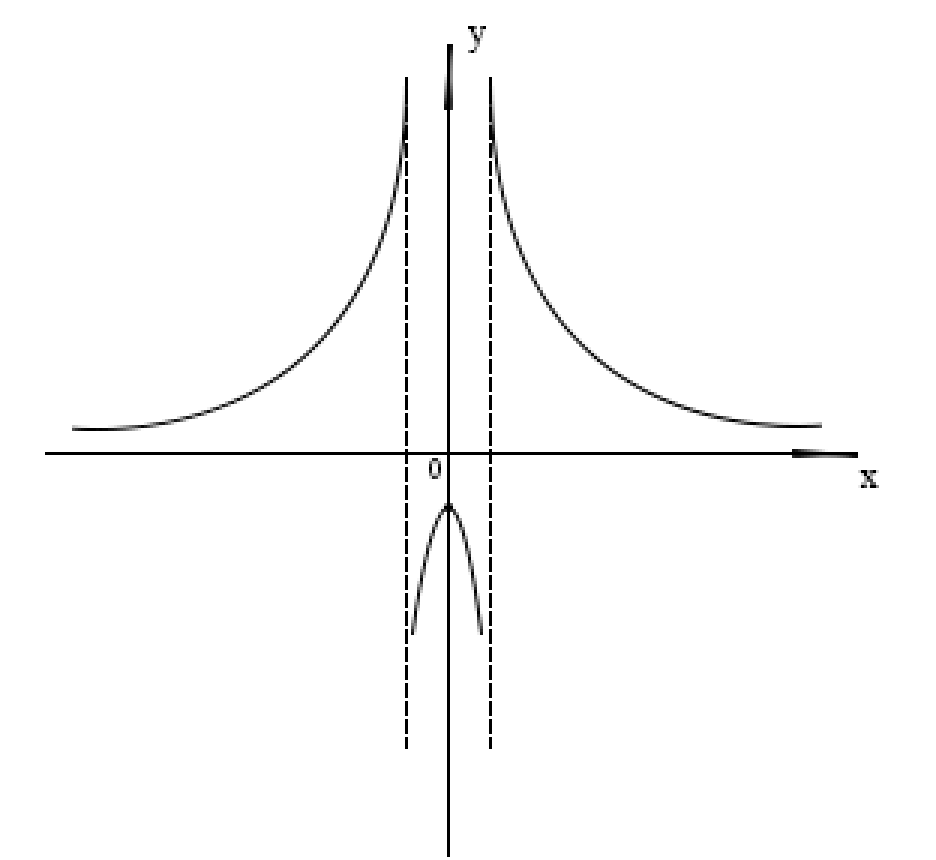 Задача 11 (109) Вычислить неопределенные интегралы. 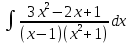 Используем метод разложения на простейшие. Разложим функцию на простейшие слагаемые: 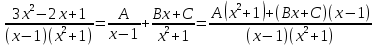 Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать: Приравняем числители и учтем, что коэффициенты при одинаковых степенях x, стоящие слева и справа должны совпадать: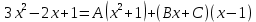 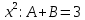 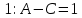 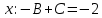 Решая ее, находим: Решая ее, находим: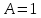 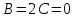 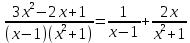 Вычисляем табличный интеграл: Вычисляем табличный интеграл: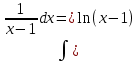 Интегрируем рациональную дробь (подводим под знак интеграла): 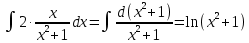 Ответ: Ответ: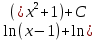 Задача 12 (139) Вычислить объем тела, образованного вращением фигуры вокруг оси Ox (задачи 131–136) или вокруг оси Oy (задачи 137– 140), ограниченной указанными линиями. Изобразить фигуру на рисунке. 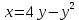 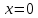 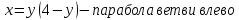
 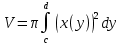 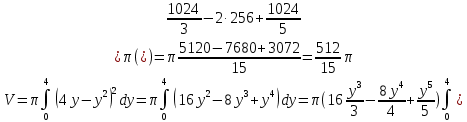 Задача 13 (199) Найти решение системы дифференциальных уравнений, удовлетворяющее заданным начальным условиям. 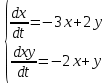 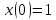 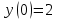 Решение: 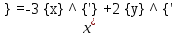 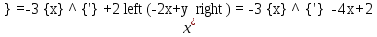 Из первого уравнения исходной системы 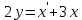 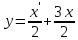 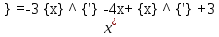 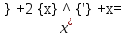 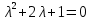 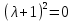 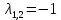 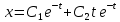 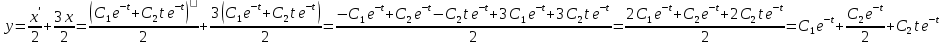 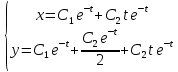 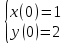 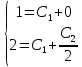 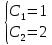 Частное решение: 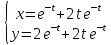 |
