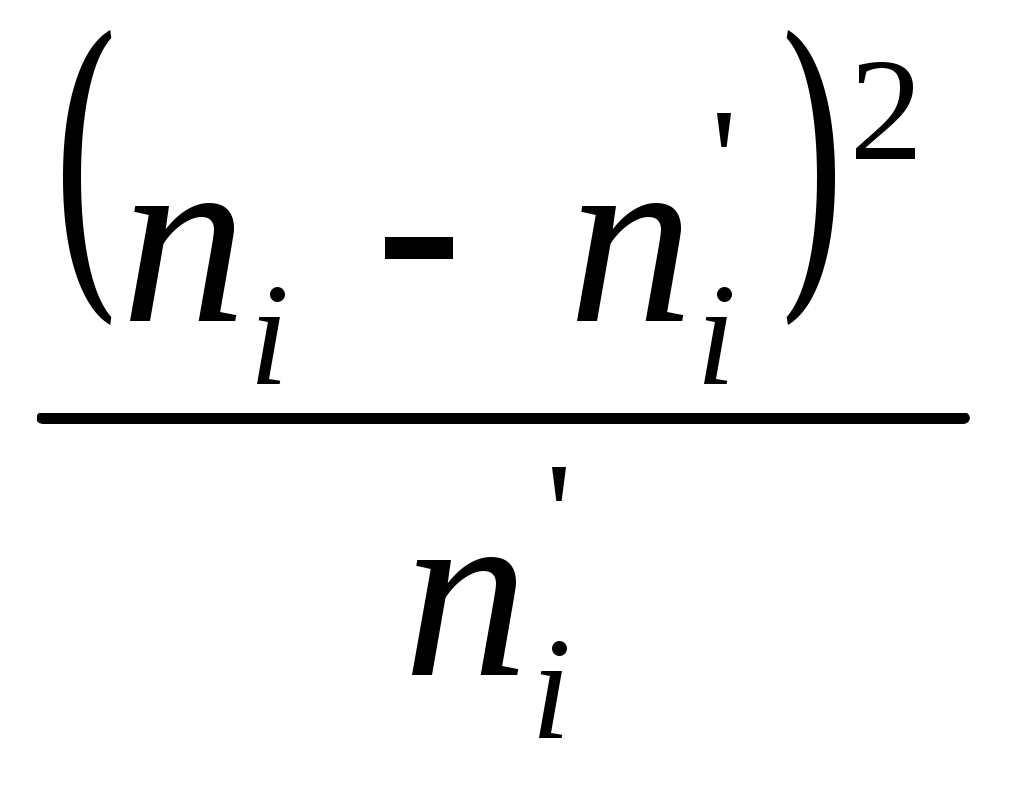Главная страница
Навигация по странице:

  • Задача 1 Исходные данные

  • Задача 2 Исходные данные

  • Сумма: 453 — 183 147

  • Задача 3

  • Задача 4

  • Задача 5

  • Задача 6

  • Задача 7

    		•

    Решение I Составим вариационный ряд. Задача 1 Исходные данные


    Скачать 308.5 Kb.
    НазваниеЗадача 1 Исходные данные
    Дата09.04.2023
    Размер308.5 Kb.
    Формат файлаdoc
    Имя файлаРешение I Составим вариационный ряд.doc
    ТипЗадача
    #1048194

    Пример решения контрольной работы по математической статистике
    Задача 1
    Исходные данные: студенты некоторой группы, состоящей из 30 человек сдали экзамен по курсу «Информатика». Полученные студентами оценки образуют следующий ряд чисел:

    4
    4
    3
    3
    2
    5
    2
    3
    3
    4

    3
    4
    4
    2
    5
    2
    3
    3
    4
    4

    3
    3
    4
    4
    2
    5
    5
    2
    3
    3


    Решение:

    I. Составим вариационный ряд


    x
    mx
    wx
    mxнак
    wxнак

    2
    6
    0,2
    6
    0,2

    3
    11
    0,37
    17
    0,57

    4
    9
    0,3
    26
    0,87

    5
    4
    0,13
    30
    1

    Итого:
    30
    1
    —
    —


    II. Графическое представление статистических сведений.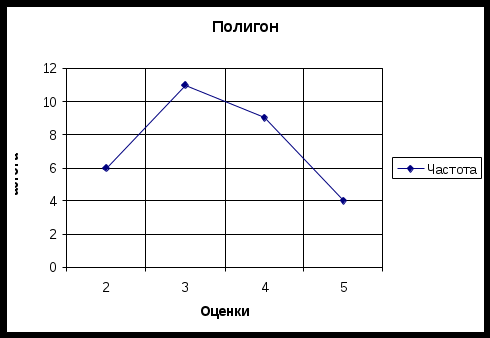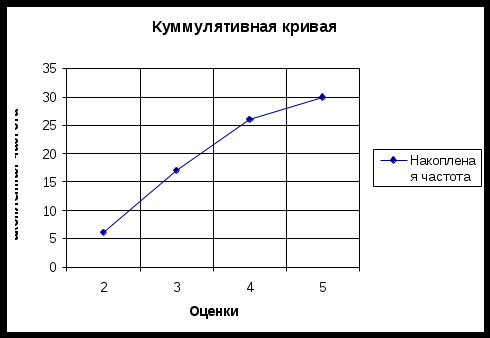





    III. Числовые характеристики выборки.

    1. Среднее арифметическое



    2. Среднее геометрическое



    3. Мода

    4. Медиана

    222222333333333 | 334444444445555



    5. Выборочная дисперсия



    6. Выборочное стандартное отклонение



    7. Коэффициент вариации



    8. Ассиметрия



    9. Коэффициент ассиметрии



    10. Эксцесс



    11. Коэффициент эксцесса


    Задача 2
    Исходные данные: студенты некоторой группы написали выпускную контрольную работу. Группа состоит из 30 человек. Набранные студентами баллы образуют следующий ряд чисел


    18
    10
    17
    13
    15
    15
    14
    17
    20
    19

    15
    15
    14
    13
    16
    16
    12
    11
    13
    14

    19
    20
    15
    16
    15
    16
    14
    16
    13
    12


    Решение

    I. Так как признак принимает много различных значений, то для него построим интервальный вариационный ряд. Для этого сначала зададим величину интервала h. Воспользуемся формулой Стэрджера



    Составим шкалу интервалов. При этом за верхнюю границу первого интервала примем величину, определяемую по формуле:



    Верхние границы последующих интервалов определим по следующей рекуррентной формуле:

    , тогда









    Построение шкалы интервалов заканчиваем, так как верхняя граница очередного интервала стала больше или равна максимальному значению выборки .

    Далее строим интервальный вариационный ряд:








    12
    4
    0,13
    4
    0,13

    14
    8
    0,27
    12
    0,4

    16
    11
    0,37
    23
    0,77

    18
    3
    0,1
    26
    0,87

    20
    4
    0,13
    30
    1

    Итого:
    30
    1
    --
    --


    II. Графическое отображение интервального вариационного ряда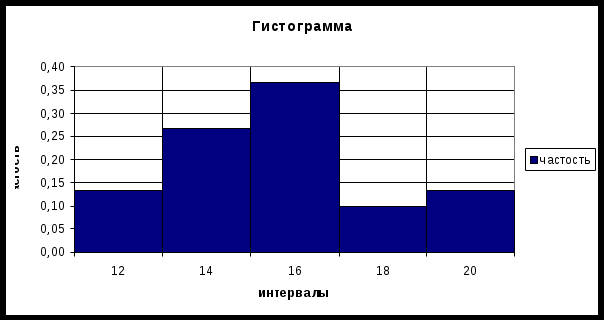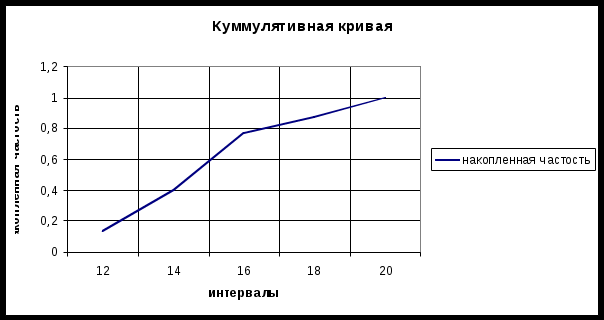



    III. Числовые характеристики выборки

    Для определения числовых характеристик выборки составим вспомогательную таблицу


    № п/п










    1
    10
    -5
    25
    -125
    625

    2
    11
    -4
    16
    -64
    256

    3
    12
    -3
    9
    -27
    81

    4
    12
    -3
    9
    -27
    81

    5
    13
    -2
    4
    -8
    16

    6
    13
    -2
    4
    -8
    16

    7
    13
    -2
    4
    -8
    16

    8
    13
    -2
    4
    -8
    16

    9
    14
    -1
    1
    -1
    1

    10
    14
    -1
    1
    -1
    1

    11
    14
    -1
    1
    -1
    1

    12
    14
    -1
    1
    -1
    1

    13
    15
    0
    0
    0
    0

    14
    15
    0
    0
    0
    0

    15
    15
    0
    0
    0
    0

    16
    15
    0
    0
    0
    0

    17
    15
    0
    0
    0
    0

    18
    15
    0
    0
    0
    0

    19
    16
    1
    1
    1
    1

    20
    16
    1
    1
    1
    1

    21
    16
    1
    1
    1
    1

    22
    16
    1
    1
    1
    1

    23
    16
    1
    1
    1
    1

    24
    17
    2
    4
    8
    16

    25
    17
    2
    4
    8
    16

    26
    18
    3
    9
    27
    81

    27
    19
    4
    16
    64
    256

    28
    19
    4
    16
    64
    256

    29
    20
    5
    25
    125
    625

    30
    20
    5
    25
    125
    625

    Сумма:
    453
    —
    183
    147
    2991


    1. Среднее арифметическое



    2. Среднее геометрическое



    3. Мода

    4. Медиана
    10 11 12 12 13 13 13 13 14 14 14 14 15 15 15 |15 15 15 16 16 16 16 16 17 17 18 19 19 20 20



    5. Выборочная дисперсия



    6. Выборочное стандартное отклонение



    7. Коэффициент вариации



    8. Ассиметрия


    9. Коэффициент ассиметрии



    10. Эксцесс



    11. Коэффициент эксцесса



    Задача 3

    Условие: цена деления шкалы амперметра равна 0,1 А. Показания округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.

    Решение.

    Ошибку округления отсчета можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между двумя соседними целыми делениями. Плотность равномерного распределения

    ,

    где — длина интервала, в котором заключены возможные значения Х; вне этого интервала В данной задаче длина интервала, в котором заключены возможные значения Х, равна 0,1, поэтому



    Ошибка отсчета превысит 0,02 если она будет заключена в интервале (0,02; 0,08). Тогда



    Ответ: р=0,6

    Задача 4

    Исходные данные: математическое ожидание и стандартное отклонение нормально распределенного признака Х соответственно равны 10 и 2. Найти вероятность того, чтов результате испытания Х примет значение, заключенное в интервале (12, 14).

    Решение.

    Воспользуемся формулой



    Подставив , , , получим

    .

    По таблице находим: , . Искомая вероятность

    Задача 5

    Исходные данные: непрерывный признак Х распределен по показательному закону, заданному плотностью вероятности при и при . Найти вероятность того, что в результате испытания Х попадет в интервал .

    Решение.

    Используем формулу



    Учитывая, что , по условию, ; ; , получим



    Задача 6

    Исходные данные: найти доверительный интервал для оценки с надежностью неизвестного математического ожидания нормально распределенного признака генеральной совокупности, если генеральное стандартное отклонение , выборочная средняя , объем выборки .

    Решение.

    Требуется найти доверительный интервал



    Все величины, кроме , известны. Найдем из соотношения



    По таблице находим .

    Подставив , , , , окончательно получим доверительный интервал



    Задача 7

    Исходные данные: используя критерий Пирсона, при уровне значимости установить, случайно или значимо расхождение между эмпирическими частотами и теоретическими частотами , которые вычислены, исходя из гипотезы о нормальном распределении генеральной совокупности Х:
    8
    16
    40
    72
    36
    18
    10



    6
    18
    36
    76
    39
    18
    7


    Решение.

    Найдем наблюдаемое значение критерия Пирсона: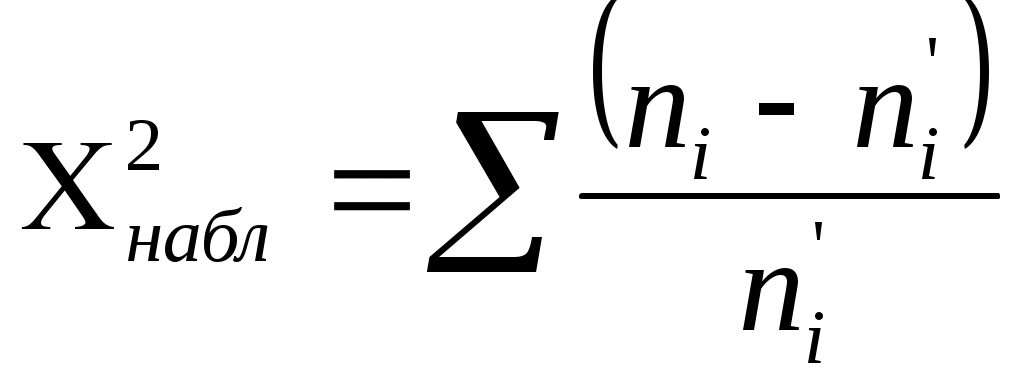



    Для этого составим расчетную таблицу










    1
    8
    6
    2
    4
    0,667

    2
    16
    18
    -2
    4
    0,222

    3
    40
    36
    4
    16
    0,444

    4
    72
    76
    -4
    16
    0,211

    5
    36
    39
    -3
    9
    0,231

    6
    18
    18
    0
    0
    0

    7
    10
    7
    3
    9
    1,286



    200












    По таблице критических точек распределения , по уровню значимости и числу степеней свободы находим критическую точку . Так как , то нет оснований отвергнуть гипотезу о нормальном распределении генеральной совокупности. Другими словами, расхождение между эмпирическими и теоретическими частотами незначимо (случайно).

    написать администратору сайта