Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Южно-Уральский государственный университет» Политехнический институт Факультет «Автотранспортный» Кафедра «Автомобильный транспорт» Задача № 1 КАЧЕСТВЕННЫЙ АНАЛИЗ РАБОТЫ ПОДШИПНИКОВ КОЛЕНЧАТОГО ВАЛА ДВС Проверил: /Задорожная Е.А./ 2023 г. Автор работы: студент группы П-416 /Ганиев Э.В. / 2023 г.
Исходные данные:
Вариант Кn43244
Диаметр опоры D = 74,5 мм
Диаметральный установочный зазор ∆ = 0,092 мм
Относительный эксцентриситет. χ = 0,8
Число оборотов коленчатого вала ДВС n= 1100,1500,1900,2500,3200 об/мин
Коэффициент динамической вязкости масла .........𝜇 = 0,0061 Па ∙ с
Безразмерная скорость поступательного движения
шипа в подшипнике 𝑑χ/dt = 0,2
........................................................................................ B = 25,7 мм
Система координат показана на рис.1.
Основная цель расчетов. Восстановить внешнюю силу, действующую на шип для двух случаев нагружения: статического и динамического. Определить влияние оборотов коленчатого вала на расчетные характеристики.
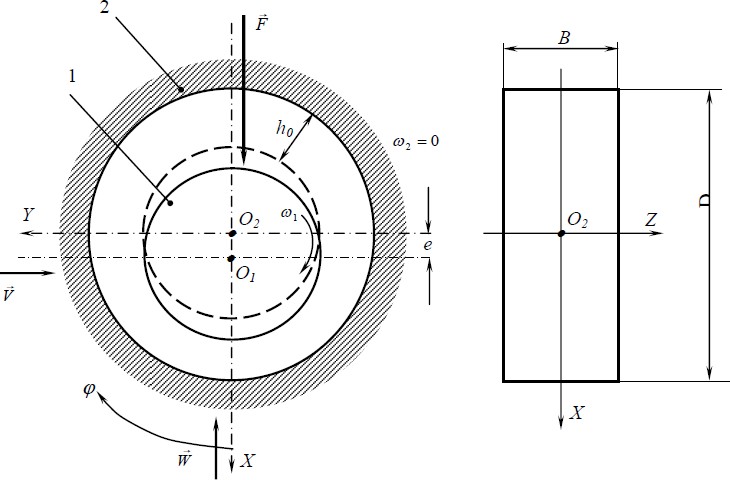
Рисунок 1 – Модель короткой опоры: B – ширина опоры, D – диаметр подшипника 2 ; 1 – шип, O1O2 – линия центров, e – эксцентриситет, W,V – проекции главного вектора сил гидродинамического давления слоя смазки на шип, O2XYZ – система координат, ϕ– угловая координата, h0 – радиальный зазор
Порядок расчета:
Расчет безразмерных входных параметров методики
Относительная длина опоры:
α = B/(2D) = 25,7/(2*74,5) = 0,1724
Угловая скорость:
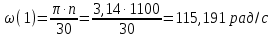
Относительная величина зазора:
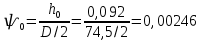
Масштаб угловой скорости:
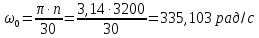 , ,
где n берется при режиме максимальной мощности Nmax, (n=3200 об/мин)
Безразмерная угловая скорость:
Безразмерная величина динамической вязкости: 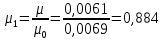 где µ 0 – вязкость масла при 100 С o; Скоростные параметры при δ = 0: G1 = ω1(1) = 0,343; E = 2·dχ/dt = 2· 0,2 = 0,4; Относительный эксцентриситет: 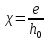 Масштаб для давления: 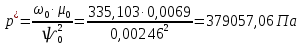
Расчет гидродинамических характеристик смазочного слоя проводится при варьировании n = 1100; 1500; 1900; 2500; 3200 для случая статического нагружения E = 0 и для случая динамического нагружения при E=0,4
А. Установить границы несущей области смазочного слоя (в градусах):
Для Е = 0, 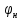 и и 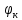 рассчитываются по формулам: рассчитываются по формулам:
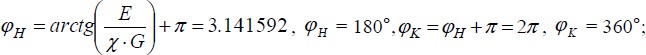
Для Е = 0,4:
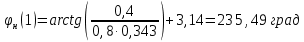
𝜑к (1) = 𝜑н (1) + 𝜋 = 235,49 + 180 = 415,49 град
Б. Рассчитать распределение давлений по угловой координате φ в центральном сечении опоры z = 0:
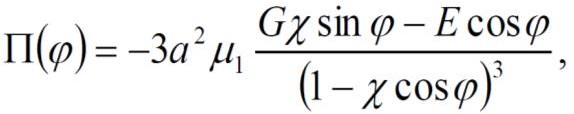
Изменяя 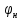 < <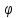 < < 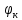 c шагом 10o. Расчетные значения заносим в таблицу 1 и 2. c шагом 10o. Расчетные значения заносим в таблицу 1 и 2.
Таблица 1 – Результаты расчетов, при Е=0
n=1100
|
n=1500
|
n=1900
|
n=2500
|
n=3200
|
|
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
|
180
|
3,141593
|
-4,55827E-19
|
180
|
3,141593
|
-6,21582E-19
|
180
|
3,141593
|
-7,87337E-19
|
180
|
3,141593
|
-1,03597E-18
|
180
|
3,141593
|
-1,32604E-18
|
|
190
|
3,316126
|
0,000659338
|
190
|
3,316126
|
0,000899097
|
190
|
3,316126
|
0,001138857
|
190
|
3,316126
|
0,001498496
|
190
|
3,316126
|
0,001918074
|
|
200
|
3,490659
|
0,001380577
|
200
|
3,490659
|
0,001882605
|
200
|
3,490659
|
0,002384633
|
200
|
3,490659
|
0,003137675
|
200
|
3,490659
|
0,004016224
|
|
210
|
3,665191
|
0,002236484
|
210
|
3,665191
|
0,003049751
|
210
|
3,665191
|
0,003863018
|
210
|
3,665191
|
0,005082918
|
210
|
3,665191
|
0,006506136
|
|
220
|
3,839724
|
0,003324495
|
220
|
3,839724
|
0,004533402
|
220
|
3,839724
|
0,005742309
|
220
|
3,839724
|
0,00755567
|
220
|
3,839724
|
0,009671257
|
|
230
|
4,014257
|
0,004787478
|
230
|
4,014257
|
0,006528379
|
230
|
4,014257
|
0,008269279
|
230
|
4,014257
|
0,010880631
|
230
|
4,014257
|
0,013927208
|
|
240
|
4,18879
|
0,006848176
|
240
|
4,18879
|
0,009338422
|
240
|
4,18879
|
0,011828668
|
240
|
4,18879
|
0,015564037
|
240
|
4,18879
|
0,019921967
|
|
250
|
4,363323
|
0,009869578
|
250
|
4,363323
|
0,013458515
|
250
|
4,363323
|
0,017047453
|
250
|
4,363323
|
0,022430859
|
250
|
4,363323
|
0,0287115
|
|
260
|
4,537856
|
0,014464448
|
260
|
4,537856
|
0,019724248
|
260
|
4,537856
|
0,024984047
|
260
|
4,537856
|
0,032873746
|
260
|
4,537856
|
0,042078395
|
|
270
|
4,712389
|
0,021698435
|
270
|
4,712389
|
0,029588774
|
270
|
4,712389
|
0,037479114
|
270
|
4,712389
|
0,049314624
|
270
|
4,712389
|
0,063122719
|
|
280
|
4,886922
|
0,03346934
|
280
|
4,886922
|
0,045640009
|
280
|
4,886922
|
0,057810678
|
280
|
4,886922
|
0,076066682
|
280
|
4,886922
|
0,097365353
|
|
290
|
5,061455
|
0,053200488
|
290
|
5,061455
|
0,07254612
|
290
|
5,061455
|
0,091891752
|
290
|
5,061455
|
0,1209102
|
290
|
5,061455
|
0,154765056
|
|
300
|
5,235988
|
0,086997202
|
300
|
5,235988
|
0,118632548
|
300
|
5,235988
|
0,150267894
|
300
|
5,235988
|
0,197720913
|
300
|
5,235988
|
0,253082768
|
|
310
|
5,410521
|
0,145007523
|
310
|
5,410521
|
0,197737531
|
310
|
5,410521
|
0,25046754
|
310
|
5,410521
|
0,329562552
|
310
|
5,410521
|
0,421840067
|
|
320
|
5,585054
|
0,240330835
|
320
|
5,585054
|
0,327723866
|
320
|
5,585054
|
0,415116897
|
320
|
5,585054
|
0,546206444
|
320
|
5,585054
|
0,699144248
|
|
330
|
5,759587
|
0,374300984
|
330
|
5,759587
|
0,510410433
|
330
|
5,759587
|
0,646519882
|
330
|
5,759587
|
0,850684055
|
330
|
5,759587
|
1,08887559
|
|
340
|
5,934119
|
0,485102839
|
340
|
5,934119
|
0,661503871
|
340
|
5,934119
|
0,837904904
|
340
|
5,934119
|
1,102506452
|
340
|
5,934119
|
1,411208259
|
|
350
|
6,108652
|
0,394590116
|
350
|
6,108652
|
0,538077431
|
350
|
6,108652
|
0,681564746
|
350
|
6,108652
|
0,896795718
|
350
|
6,108652
|
1,147898519
|
|
360
|
6,283185
|
6,64595E-16
|
360
|
6,283185
|
9,06266E-16
|
360
|
6,283185
|
1,14794E-15
|
360
|
6,283185
|
1,51044E-15
|
360
|
6,283185
|
1,93337E-15
|
|
Таблица 2– Результаты расчетов, при E=0,4
n=1100
|
n=1500
|
n=1900
|
n=2500
|
n=3200
|
|
|
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
ϕ, град
|
ϕ,рад
|
П
|
|
|
235,4915
|
4,1101
|
2,141E-18
|
226,8476
|
3,9592
|
0,0000000
|
220,1009
|
3,8415
|
0,0000000
|
212,6192
|
3,7109
|
0,0000000
|
206,5651
|
3,6052
|
0,000000
|
|
|
245,4915
|
4,2846
|
2,815E-03
|
236,8476
|
4,1338
|
0,0025291
|
230,1009
|
4,0160
|
0,0024559
|
222,6192
|
3,8854
|
0,0025355
|
216,5651
|
3,7798
|
0,002765
|
|
|
255,4915
|
4,4592
|
7,573E-03
|
246,8476
|
4,3083
|
0,0065138
|
240,1009
|
4,1906
|
0,0061233
|
232,6192
|
4,0600
|
0,0061065
|
226,5651
|
3,9543
|
0,006482
|
|
|
265,4915
|
4,6337
|
1,595E-02
|
256,8476
|
4,4828
|
0,0130975
|
250,1009
|
4,3651
|
0,0118957
|
242,6192
|
4,2345
|
0,0114370
|
236,5651
|
4,1288
|
0,011798
|
|
|
275,4915
|
4,8082
|
3,126E-02
|
266,8476
|
4,6574
|
0,0244389
|
260,1009
|
4,5396
|
0,0213972
|
252,6192
|
4,4090
|
0,0197880
|
246,5651
|
4,3034
|
0,019806
|
|
|
285,4915
|
4,9828
|
6,035E-02
|
276,8476
|
4,8319
|
0,0447681
|
270,1009
|
4,7142
|
0,0376937
|
262,6192
|
4,5836
|
0,0334444
|
256,5651
|
4,4779
|
0,032418
|
|
|
295,4915
|
5,1573
|
1,177E-01
|
286,8476
|
5,0064
|
0,0826648
|
280,1009
|
4,8887
|
0,0667847
|
272,6192
|
4,7581
|
0,0566994
|
266,5651
|
4,6524
|
0,053109
|
|
|
305,4915
|
5,3318
|
2,343E-01
|
296,8476
|
5,1810
|
0,1560248
|
290,1009
|
5,0632
|
0,1207930
|
282,6192
|
4,9326
|
0,0979028
|
276,5651
|
4,8270
|
0,088430
|
|
|
315,4915
|
5,5064
|
4,761E-01
|
306,8476
|
5,3555
|
0,3025701
|
300,1009
|
5,2377
|
0,2247641
|
292,6192
|
5,1072
|
0,1737651
|
286,5651
|
5,0015
|
0,151106
|
|
|
325,4915
|
5,6809
|
9,679E-01
|
316,8476
|
5,5300
|
0,5993344
|
310,1009
|
5,4123
|
0,4303109
|
302,6192
|
5,2817
|
0,3182316
|
296,5651
|
5,1760
|
0,266422
|
|
|
335,4915
|
5,8554
|
1,873E+00
|
326,8476
|
5,7046
|
1,1831253
|
320,1009
|
5,5868
|
0,8373199
|
312,6192
|
5,4562
|
0,5989925
|
306,5651
|
5,3506
|
0,484687
|
|
|
345,4915
|
6,0300
|
3,138E+00
|
336,8476
|
5,8791
|
2,1986768
|
330,1009
|
5,7613
|
1,5994604
|
322,6192
|
5,6308
|
1,1379248
|
316,5651
|
5,5251
|
0,901051
|
|
|
355,4915
|
6,2045
|
3,996E+00
|
346,8476
|
6,0536
|
3,4717501
|
340,1009
|
5,9359
|
2,7898965
|
332,6192
|
5,8053
|
2,0871338
|
326,5651
|
5,6996
|
1,664277
|
|
|
365,4915
|
6,3790
|
3,473E+00
|
356,8476
|
6,2282
|
4,0682716
|
350,1009
|
6,1104
|
3,9443523
|
342,6192
|
5,9798
|
3,3894801
|
336,5651
|
5,8742
|
2,872748
|
|
|
375,4915
|
6,5536
|
2,048E+00
|
366,8476
|
6,4027
|
3,1947083
|
360,1009
|
6,2849
|
3,9368397
|
352,6192
|
6,1544
|
4,2659960
|
346,5651
|
6,0487
|
4,152218
|
|
|
385,4915
|
6,7281
|
8,925E-01
|
376,8476
|
6,5772
|
1,6809576
|
370,1009
|
6,4595
|
2,5567410
|
362,6192
|
6,3289
|
3,6138526
|
356,5651
|
6,2232
|
4,317094
|
|
|
395,4915
|
6,9026
|
3,091E-01
|
386,8476
|
6,7518
|
0,6309697
|
380,1009
|
6,6340
|
1,0890579
|
372,6192
|
6,5034
|
1,8980580
|
366,5651
|
6,3978
|
2,791703
|
|
|
405,4915
|
7,0772
|
7,851E-02
|
396,8476
|
6,9263
|
0,1612675
|
390,1009
|
6,8085
|
0,2915292
|
382,6192
|
6,6780
|
0,5683343
|
376,5651
|
6,5723
|
0,966296
|
|
|
415,4915
|
7,2517
|
-2,412E-16
|
406,8476
|
7,1008
|
0,0000000
|
400,1009
|
6,9831
|
0,0000000
|
392,6192
|
6,8525
|
0,0000000
|
386,5651
|
6,746833
|
0,000000
|
|
|
В. Построить графические зависимости П(φ) для каждого из наборов величин (n, Е), используя результаты расчетов, приведенные в таблицах 1 и 2. Графические зависимости представлены на рисунке 2 и 3.
|
 Скачать 0.56 Mb.
Скачать 0.56 Mb.
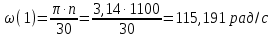
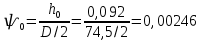
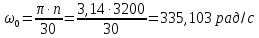 ,
,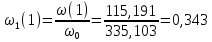
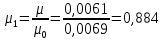
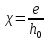
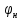 и
и 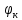 рассчитываются по формулам:
рассчитываются по формулам: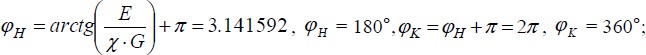
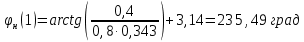
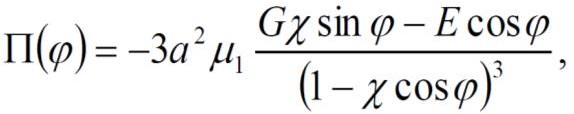
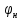 <
<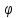 <
< 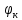 c шагом 10o. Расчетные значения заносим в таблицу 1 и 2.
c шагом 10o. Расчетные значения заносим в таблицу 1 и 2.