Контрольная работа Статистика - вариант 2. Задача 1 Какие из указанных ниже группировок являются типологическими
 Скачать 411.5 Kb.
|
|
Задача 1 Какие из указанных ниже группировок являются типологическими: а) населения по возрасту; б) работников по тарифному разряду; в) населения по общественным группам; г) населения, занятого по отраслям; д) производство средств производства и предметов потребления? Назовите виды группировок и основные их назначения. Все из указанных выше группировок являются типологическими. Для решения задач, возникающих в ходе научного статистического исследования, применяют следующие виды группировок. Типологическая группировка решает задачу выявления и характеристики социально-экономических типов. При этом виде в качестве группировочных выступают существенные признаки, которые и различают выделенные типы или группы по существу. Этот вид группировок в значительной степени определяется представлениями экспертов о том, какие типы могут встретиться в изучаемой совокупности. Структурные группировки характеризуют структуру совокупности по какому-либо одному не обязательно существующему признаку. Число интервалов в таких группировках должно быть оптимальным. На основе данной группировки можно изучать динамику структуры совокупности. К структурным группировкам относятся группировки хозяйств по объему продукции, населения по размеру среднедушевого дохода. Аналитическая группировка характеризует взаимосвязь между двумя и более признаками, один из которых рассматривается в качестве результата, а другой как фактор. Простая группировка представляет собой группировку по одному признаку. Сложная группировка — это группировка по двум или нескольким признакам. Комбинационная группировка, в основании которой лежат несколько признаков, т. е. группы, образованные по одному признаку, делятся на подгруппы — по второму, а последние — по третьему признаку и т. д. Данный вид группировки позволяет выявить и сравнить различия и связи между исследуемыми признаками, которые нельзя обнаружить на основе изолированных группировок по ряду группировочных признаков. Многомерная группировка основана на измерении сходства или различия между объектами, т. е. единицы, отнесенные к одному классу, различаются между собой меньше, чем единицы, отнесенные к различным классам. Задача многомерной группировки сводится к выделению или сгущению объектов в n-мерном пространстве. Задача 2 Определите динамику и структуру изменения объема продукции в квартальном разрезе и в целом за год двух предприятий по следующим исходным данным:
Проанализируйте полученные результаты. Решение. Структура производства продукции предприятия № 1 в квартальном разрезе:
Структура производства продукции предприятия № 2 в квартальном разрезе:
Таким образом, как на первом, так и на втором предприятии большая часть произведенной за год продукции выпущено в четвертом квартале. Объем производства продукции двух предприятий вместе за год составил: 460 + 630 = 1090 млрд. р. в том числе по кварталам: I квартал: 110 + 150 = 260 млрд. р. II квартал: 120 + 150 = 270 млрд. р. III квартал: 100 + 160 = 260 млрд. р. IV квартал: 130 + 170 = 300 млрд. р. Таким образом, структура объема производства выглядит следующим образом:
Динамика объема продукции по кварталам представлена в таблице:
Таким образом, объем производства в четвертом квартале превысил значение производства в первом квартале на 40 млрд.р. (или на 15,4%). Задача 3 Определите средний возраст работников и показатели вариации по следующим данным:
Проанализируйте полученные результаты. Решение. В условии задачи дается интервальный вариационный ряд распределения с открытыми интервалами. Чтобы определить средний объем продукции, нужно от интервального ряда перейти к дискретному, т.е. найти середину каждого интервала как полусумму нижней и верхней границ. При этом величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы - к величине интервала предпоследней группы. После вышесказанных преобразований исходная таблица будет выглядеть следующим образом:
Средний объем возраст работников по предприятию рассчитаем по формуле средней арифметической взвешенной:   лет.Для характеристики размеров колеблемости признаков в статистике используют ряд показателей. Рассчитаем следующие показатели: - дисперсия: 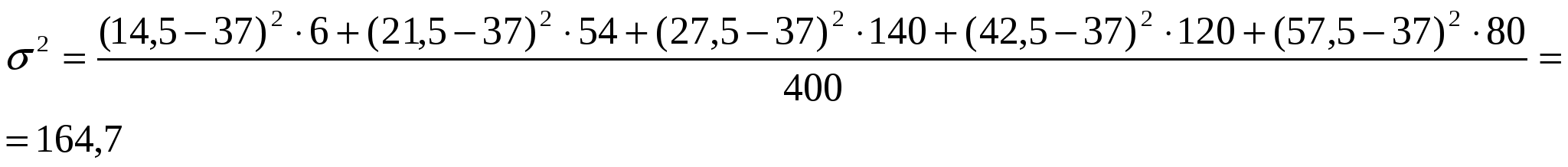 - среднее квадратическое отклонение: σ =  = 12,8.- коэффициент вариации рассчитывается по формуле:  Так как коэффициент вариации больше 33 %, это говорит о неоднородности изучаемой совокупности. Задача 4 На основании данных о распределении предприятий по среднегодовой численности работников одной из отраслей народного хозяйства: 1) определите, моду и медиану; 2) постройте гистограмму; 3) оцените характер асимметрии.
Решение. Перейдем от интервального ряда перейти к дискретному.
Таким образом, среднее число работников:  чел.Разновидностью средней являются мода и медиана. Эти величины также используются в качестве характеристик вариационного ряда. Мода (Мо) – варианта, встречающаяся в ряду распределения чаще всего, т.е. варианта, которой соответствует наибольшая частота. Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой расположена наибольшая частота, и будет модой. В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Вычисление моды производится по следующей формуле:  где  - начало (нижняя граница) модального интервала;  - величина интервала;  - частота модального интервала;  - частота интервала, предшествующего модальному;  - частота интервала, следующего за модальным.Таким образом, мода равна:  чел.Медиана  – варианта, находящаяся в середине ранжированного ряда распределения. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Серединная варианта и будет являться медианой. Расчет медианы для интервального ряда производится по формуле:  – начало (нижняя граница) медианного интервала; iMe – величина интервала;  – сумма всех частот ряда;  – сумма накопленных частот вариантов до медианного;  – частота медианного интервала.Для определения медианного интервала необходимо определять накопленную частоту каждого последующего интервала до тех пор, пока она не превысит 1/2 суммы накопленных частот (в нашем случае – 50.)
Таким образом, медианным является интервал с границами 1000 – 5000. Медиана равна:  чел.Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Т.к.  < Мо, Me< Мо следует сделать вывод о левосторонней асимметрии ряда. Это подтверждает построенная гистограмма: 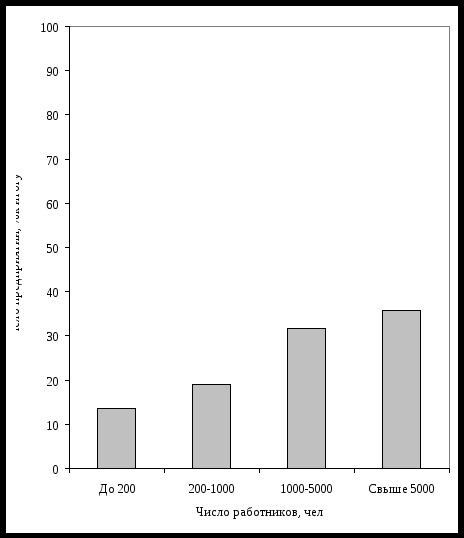 Рис. 4.1. Распределение предприятий по числу работников Задача 5 Рост выпуска продукции на предприятии за пять лет характеризуется следующими данными:
На основании этих данных исчислите: а) показатели ряда динамики (абсолютные приросты, темпы роста и темпы прироста, абсолютное значение одного процента прироста за весь период); б) средний уровень ряда; в) среднегодовой темп динамики (по абсолютным уровням ряда). Проанализируйте полученные результаты. Сделайте вывод о характере изменения выпуска продукции на данном предприятии по годам. Решение. В зависимости от задачи исследования абсолютные приросты (снижения,  ), темпы роста (снижения, Т) и темпы прироста (снижения,  ) могут быть рассчитаны с переменной базой сравнения (цепные) и постоянной базой сравнения (базисные).Абсолютные приросты: цепные ........................................  базисные......................................  Темпы роста: цепные.......................................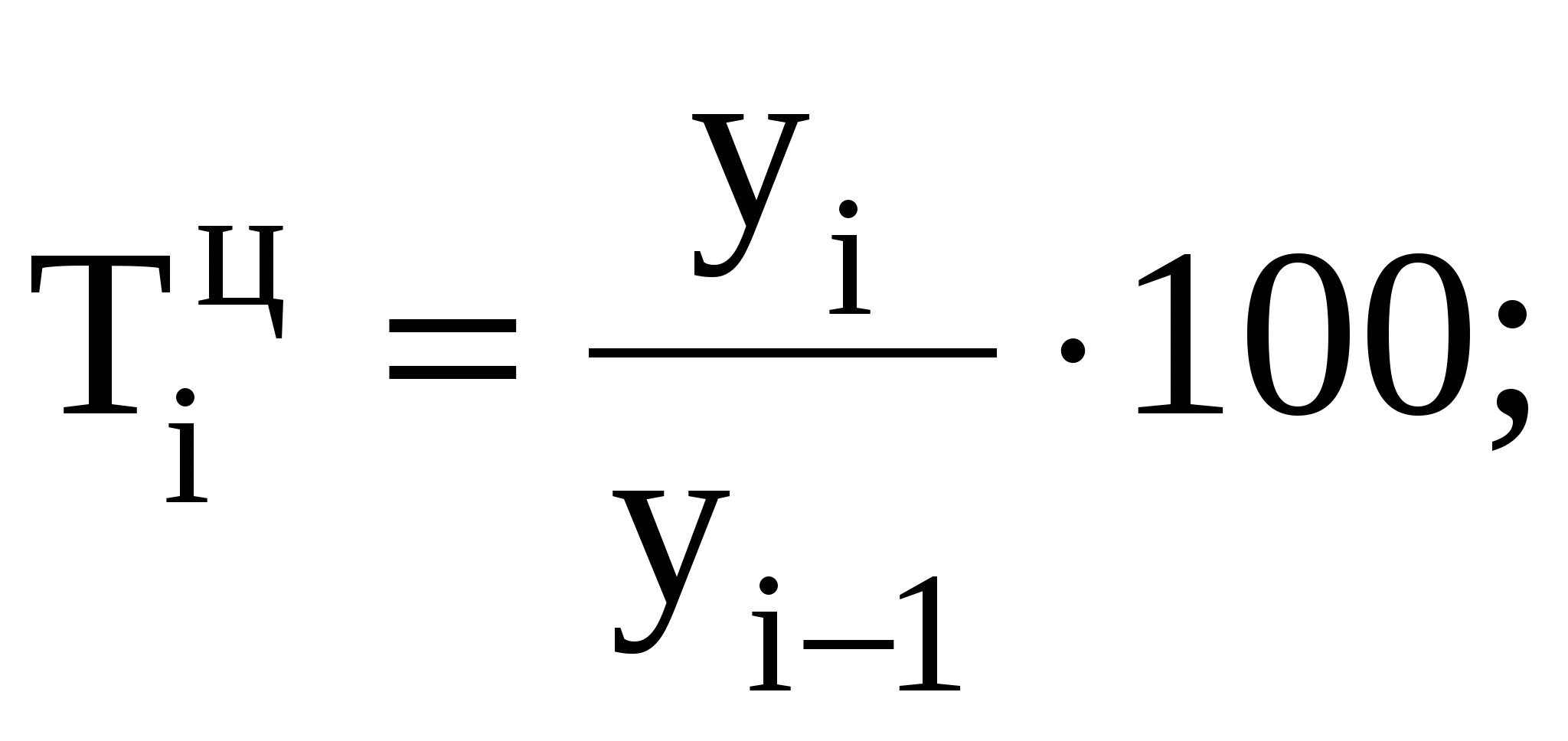....  базисные.......................................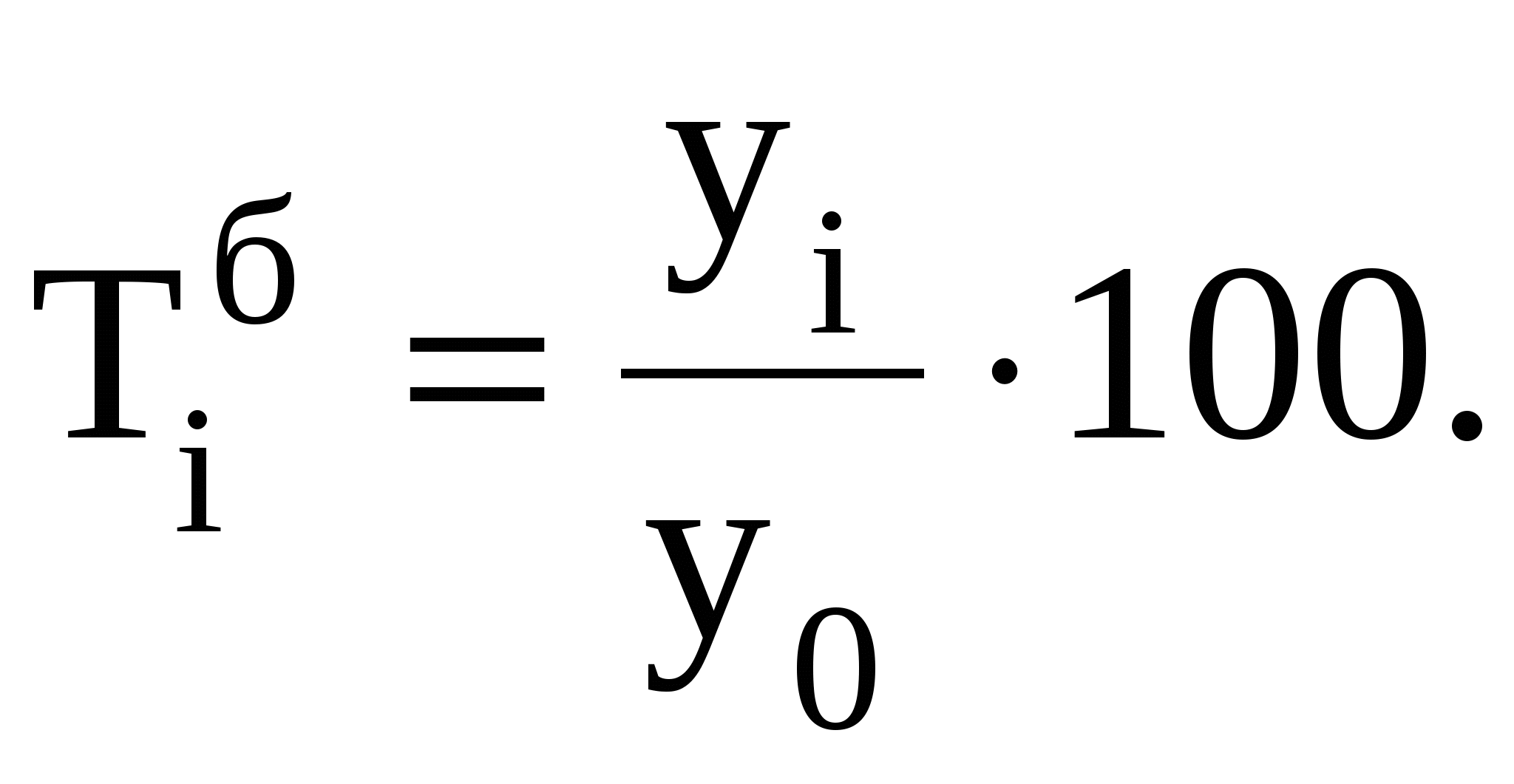...  Темпы прироста: цепные................................... 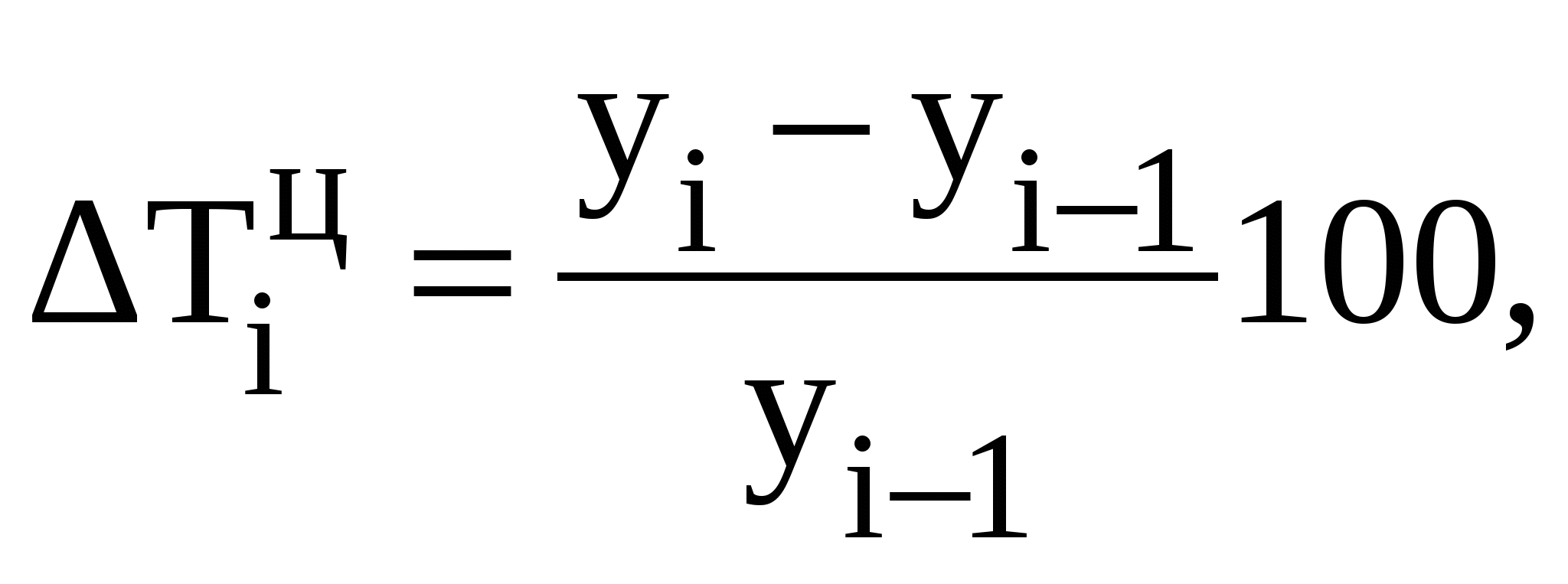 базисные.................................. 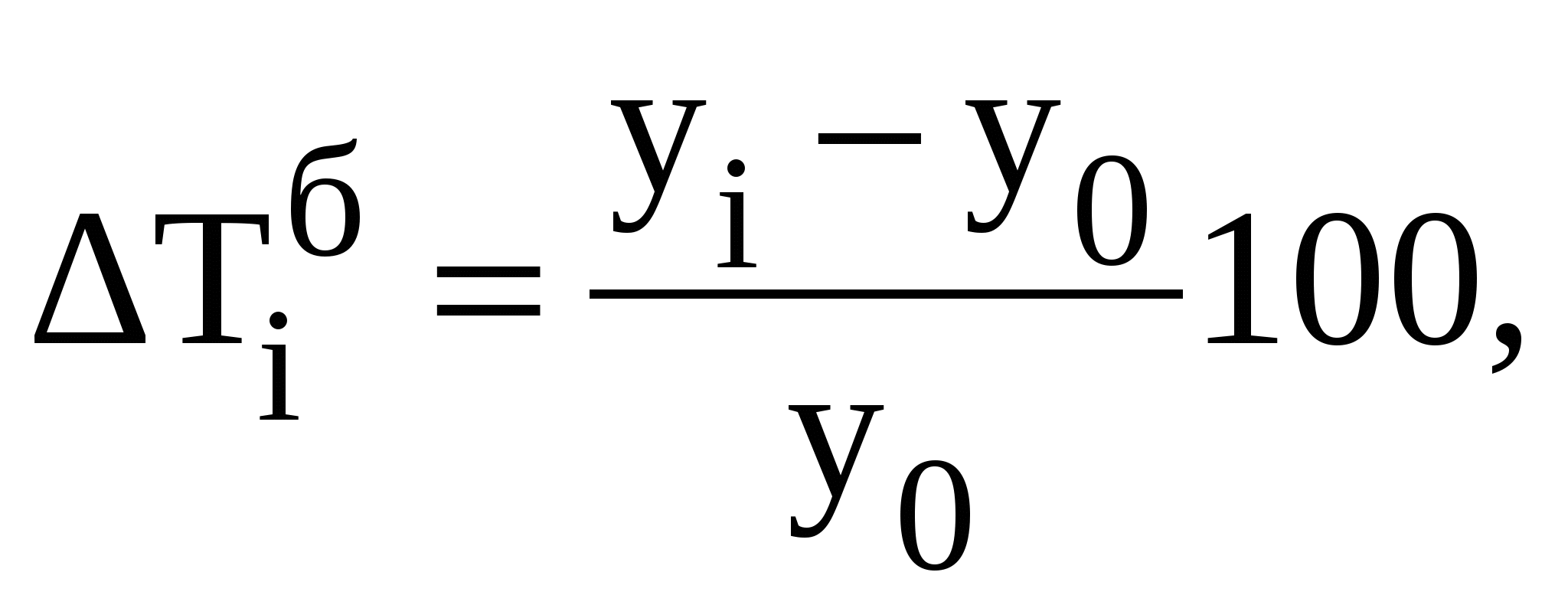  или  Абсолютное значение одного процента прироста (снижения) – это отношение абсолютного цепного прироста к соответствующему цепному темпу прироста, выраженному в процентах. Оно определяется по формуле: 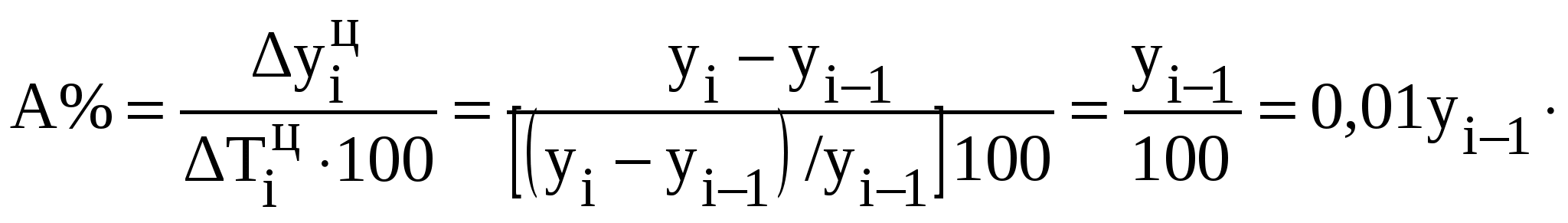 Результаты расчетов приведены в таблице:
Средний уровень ряда может быть исчислен по формуле средней арифметической простой:  млрд.р.Средний абсолютный прирост исчисляется двумя способами: 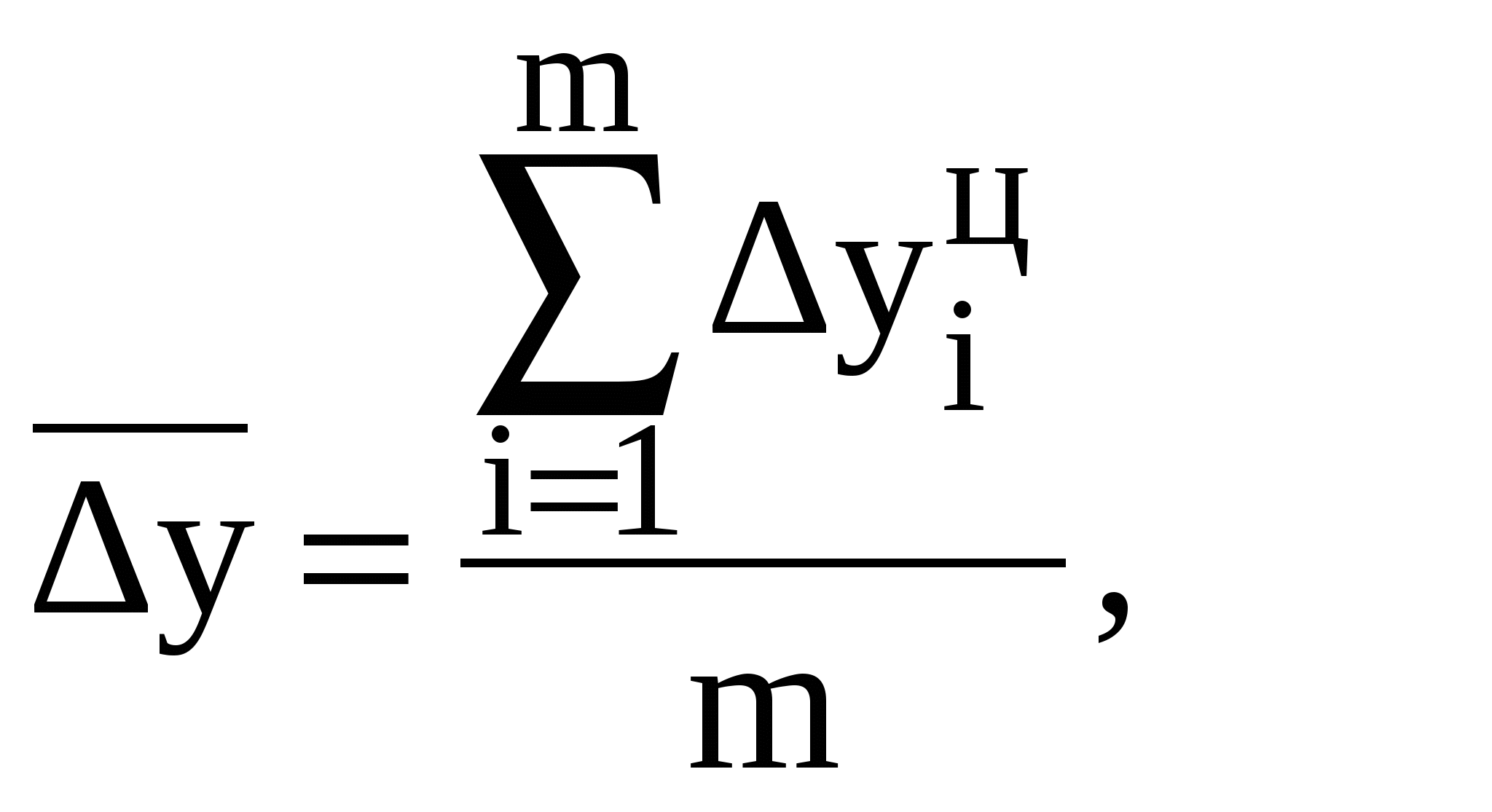 или  где  – цепные абсолютные приросты; m – число цепных абсолютных приростов.Среднегодовой абсолютный прирост производства продукции за анализируемый период равен:  (21,5 – 11,2) / 4 = 2,575 млрд.р.Изучив динамику производства продукции можно сделать следующие выводы. В целом за рассматриваемый период производство продукции увеличилось на 10,3 млрд.р. (или на 91,96 %). В среднем производство продукции за год увеличивалось на 2,575 млрд.р. Задача 6 На основании следующих данных рассчитайте общий индекс производительности труда по группе предприятий. Определите также количество работников, которое было высвобождено в результате роста производительности труда.
Решение. Общий индекс производительности труда рассчитаем по формуле:  Т.е. производительность труда увеличилась на 4%. Разность числителя и знаменателя рассчитанного индекса показывает экономию живого труда (количество высвобожденных работников) за счет роста производительности: ∆Т = 1640 – 1570 = 70 чел. Задача 7 Имеются следующие данные:
Определите: а) влияние динамики часовой выработки одного рабочего, продолжительности рабочего дня и рабочего месяца на динамику среднемесячной выработки; б) влияние каждого фактора в абсолютном выражении на функцию. Решение. Производительность труда одного работника за месяц (W) равна его среднечасовой выработке (а), умноженной на среднюю продолжительность дня (b) и на среднюю продолжительность рабочего месяца (с). W = cba. Система многофакторных индексов:   = . . Таким образом, производительность труда в базисном периоде составила: W0 = 100 . 7,7 . 20 = 15400 ед. в отчетном периоде: W1 = 120 . 7,8 . 22 = 20592 ед.  1,337 = 1,1 . 1,013 . 1,2 Абсолютное изменение выработки: ΔW = 20592 – 15400 = 5192 ед. Количество продукции (в абсолютном выражении) в расчете на одного рабочего, полученное за счет роста часовой выработки одного рабочего: ΔWа = (120 – 100)* 7,7 * 20 = 3080 ед. Количество продукции (в абсолютном выражении) в расчете на одного рабочего, полученное за счет снижения продолжительности рабочего дня: ΔWb = 120 * (7,8 – 7,7) * 20 = 240 ед. Количество продукции (в абсолютном выражении) в расчете на одного рабочего, полученное за счет снижения продолжительности рабочего месяца: ΔWс = 120* 7,8 * (22 – 20) = 1872 ед. Проверка: ΔW = ΔWа + ΔWb + ΔWс 5192 = 3080 + 240 + 1872 5192 = 5192 Задача 8 Изобразите данные задачи 2 с помощью столбиковых графиков, круговых графиков и ломаной кривой. Какой из этих графиков наиболее наглядно изображает динамику и структуру объема продукции в квартальном разрезе? Решение. Столбиковый график: 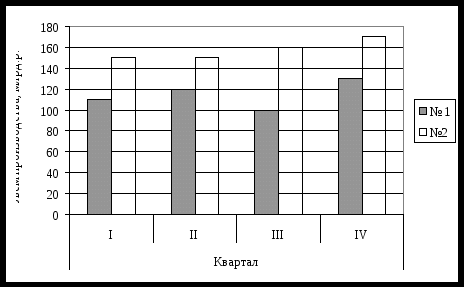 Круговой график: 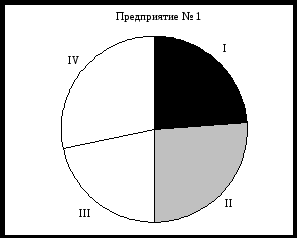 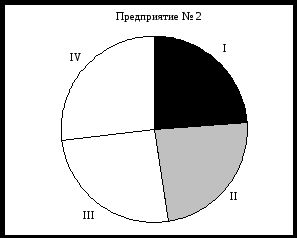 Ломаная кривая: 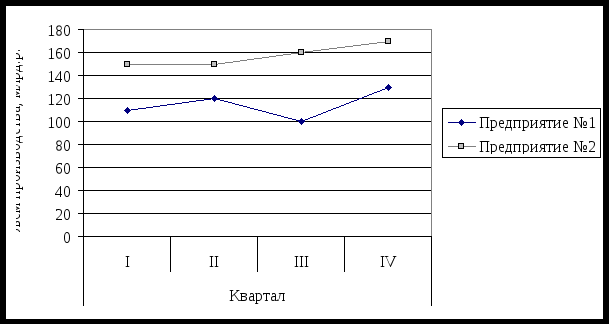 Таким образом, наиболее наглядным является график в виде ломаной кривой. Задача 9 При 20%-ной разработке (по способу случайной бесповоротной выборки) данных текущего учета населения города удельный вес жителей в возрасте свыше 60 лет составил 8%, удельный вес населения в возрасте до 16 лет - 14%, удельный вес рабочих (без членов их семей) - 18%. Определите с вероятностью 0,954: а) предельную ошибку выборки удельного веса каждой из групп жителей; б) пределы (доверительный интервал), в которых будет находиться доля каждой из указанных групп жителей; в) какова должна быть доля выборки (объем выборки), чтобы предельная ошибка в оценке доли по указанным группам жителей была не более 0,20 %. Общая численность населения города составляет 300 тыс. человек. Решение. Возможные границы генеральной доли определяется по формуле:  где w – выборочная доля (удельный вес единиц в выборке, обладающих исследуемым признаком; w = m/n)  – предельная ошибка выборочной доли (для бесповторного отбора).Так, удельный вес жителей в возрасте свыше 60 лет равен 0,08. w = 0,08. Предельная ошибка выборочной доли:  Тогда границы удельного веса данной группы:  0,031  р 0,129 Т.е. доля жителей в возрасте свыше 60 лет находится в пределах от 3,1% до 12,9%. Удельный вес населения в возрасте до 16 лет: w = 0,14. Предельная ошибка выборочной доли:  Тогда границы удельного веса данной группы: 0,078 р 0,202 Т.е. доля жителей в возрасте до 16 лет находится в пределах от 7,8% до 20,2%. Удельный вес рабочих: w = 0,18. Предельная ошибка выборочной доли:  Тогда границы удельного веса данной группы: 0,112 р 0,248 Т.е. доля рабочих находится в пределах от 11,2% до 24,8%. Необходимый объем выборки рассчитаем по формуле:  Объем выборки, чтобы предельная ошибка в оценке доли жителей в возрасте свыше 60 лет была не более 0,2%:  59 101 чел.Доля выборки = 59101 / 300000 . 100 = 19,7%. Объем выборки, чтобы предельная ошибка в оценке доли жителей в возрасте до 16 лет была не более 0,2%:  85 918 чел.Доля выборки = 85918 / 300000 . 100 = 28,6%. Объем выборки, чтобы предельная ошибка в оценке доли жителей в возрасте до 16 лет была не более 0,2%:  98 928 чел.Доля выборки = 98928 / 300000 . 100 = 33%. Задача 10 Имеются следующие данные о связи между произведенной продукцией (в отпускных ценах) и переработкой сырья по 12 предприятиям:
Составьте линейное уравнение регрессии, вычислите параметры и оцените тесноту корреляционной связи. Решение. Видно, что при росте размера предприятия возрастает фондоотдача, т.е. между этими показателями существует прямая корреляционная зависимость. Коэффициент парной корреляции определяет тесноту связи между результативным и факторным показателями:  Расчет показателя тесноты связи
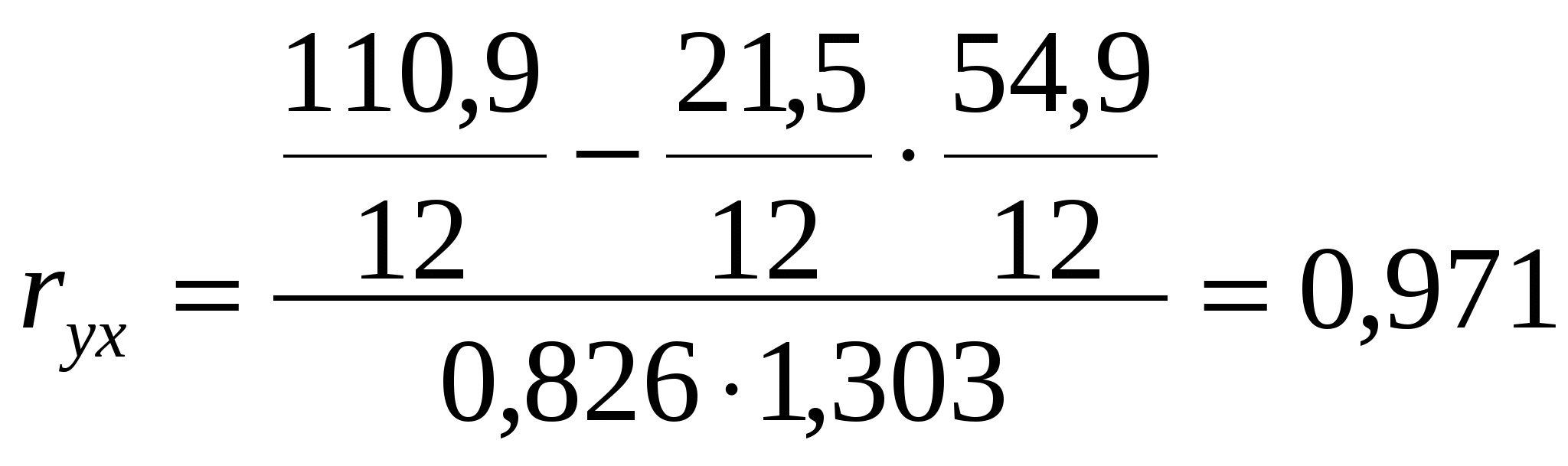 0,826 1,303 Т.к. 0<  <1, значит корреляция между x и y называется положительной, и она показывает, что с ростом одного показателя второй показатель возрастает. Связь между показателями довольно теснаяОпределим параметры a и bуравнения регрессии y = a + bх 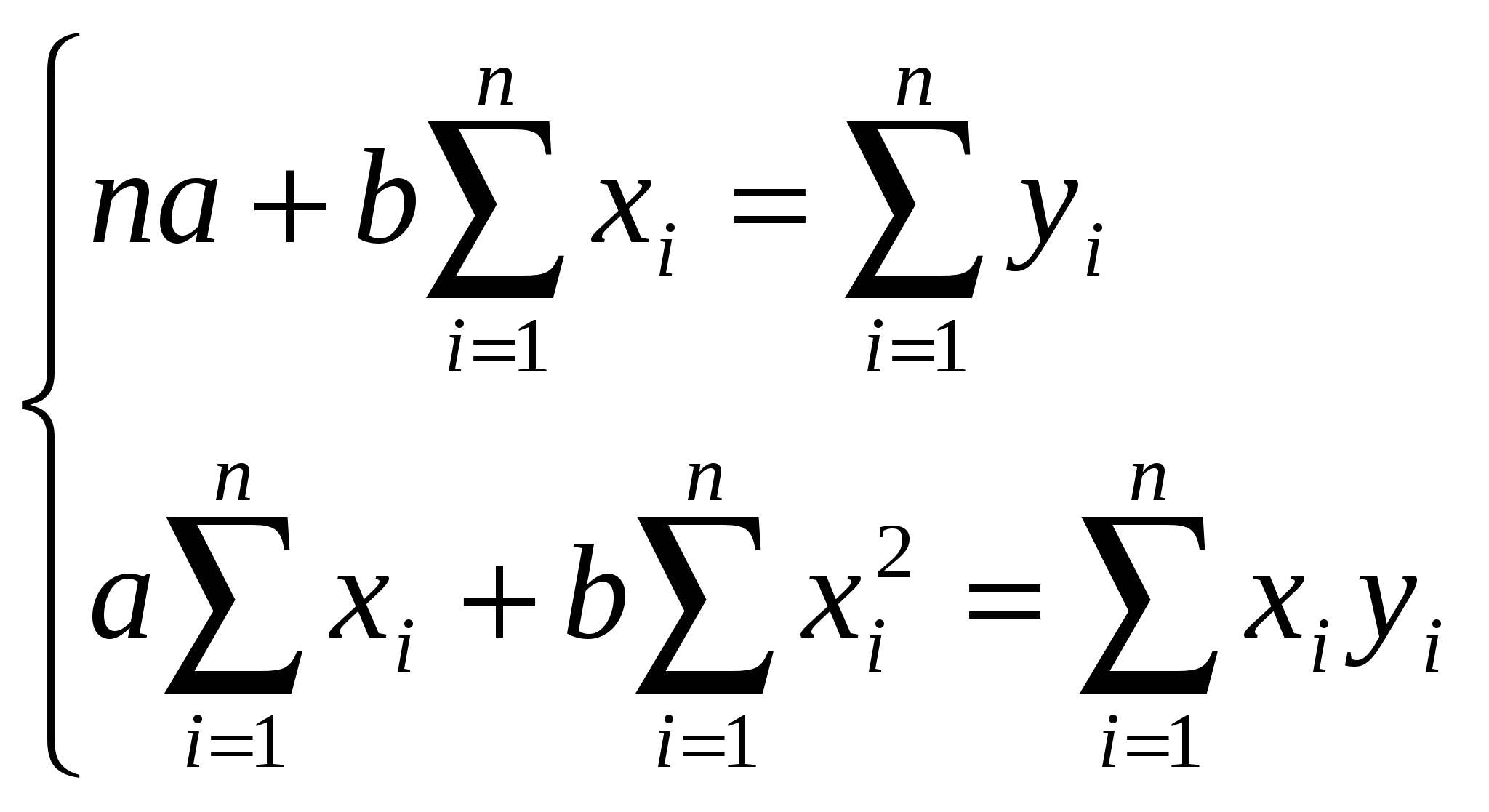 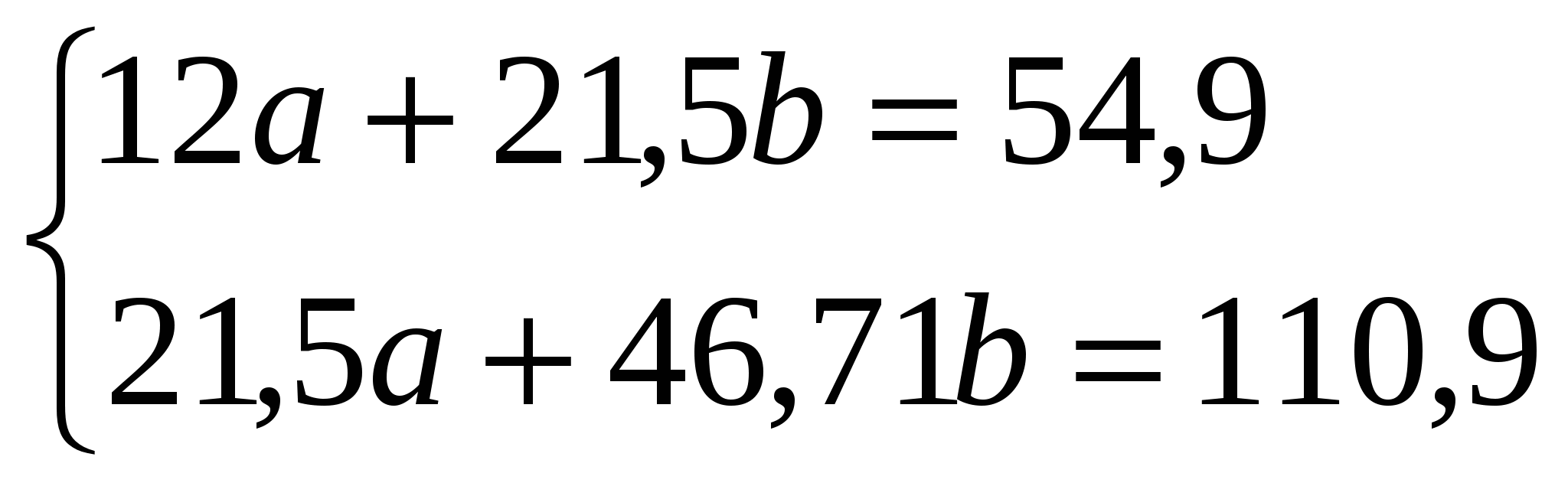 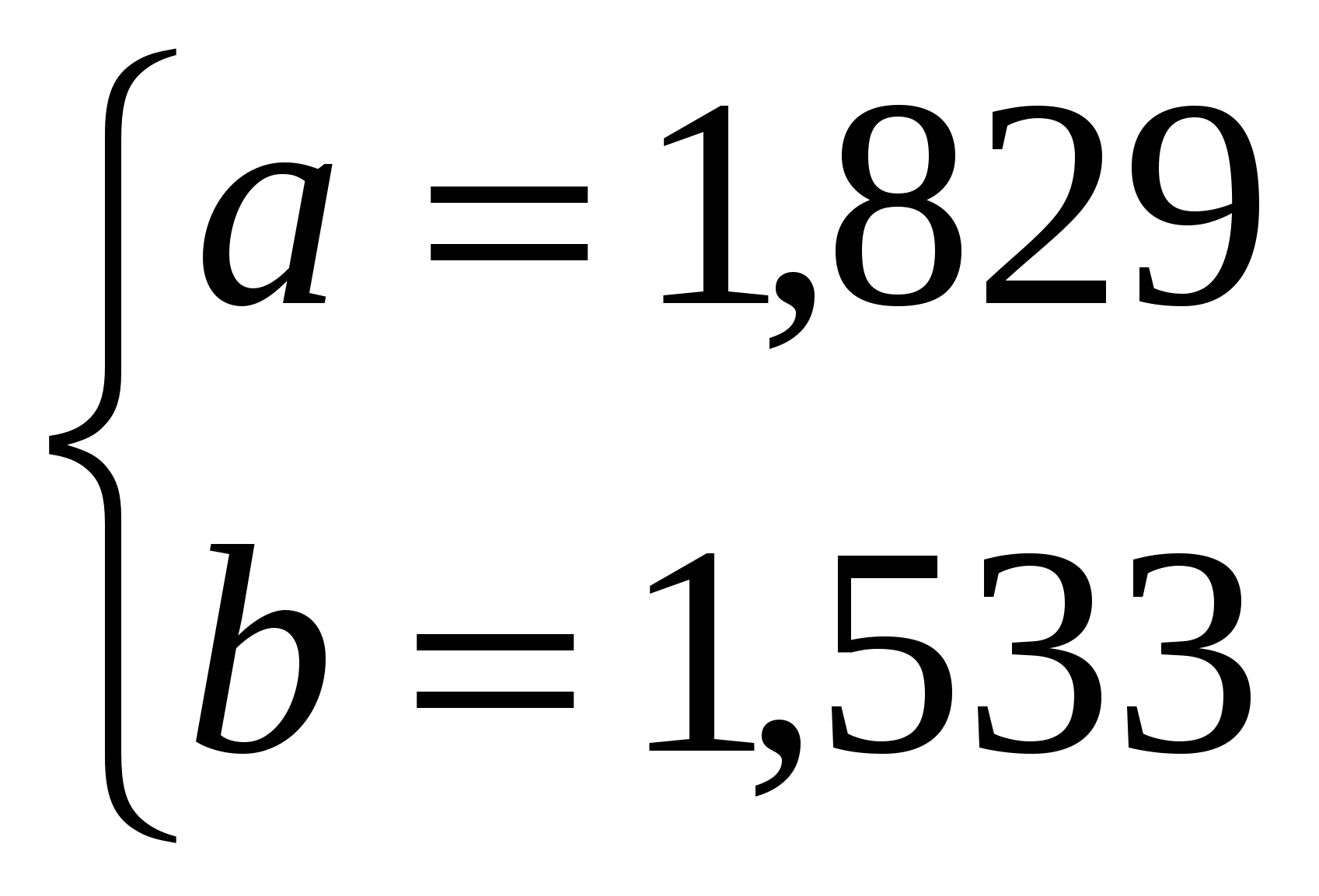 Уравнение регрессии y = 1,829 + 1,533х. Графики, соответствующие эмпирическому ряду данных и уравнению 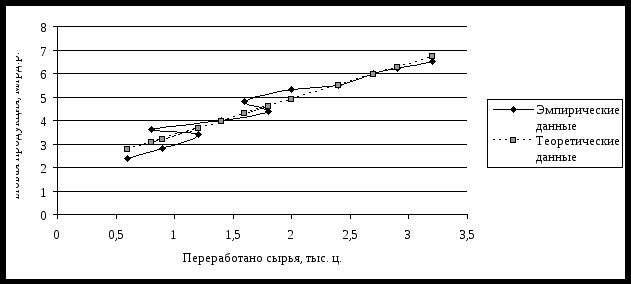 Проанализировав зависимость валовой продукции от количества переработанного сырья, можно сказать, что зависимость между этими показателями прямая и очень тесная. Это подтверждается значением коэффициента корреляции и при графическом анализе направления и тесноты связи. Список использованных источников
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
