Главная страница
Навигация по странице:

  • Раздел «СТАТИКА» Шелкунов Максим Андреевичгруппа 20 -- ТМВАРИАНТ №20Проверил: Старший преподаватель кафедры ТиОМП

  • Тихон Елена Михайловна Новополоцк, 2021ЗАДАЧА 1.1

  • Ответ

    		•

    РАсчетно графическая работа по Теоретической механике. теор мех РГР 1 вариант 20. Задача 1 определение опорных реакций балки


    Скачать 339.55 Kb.
    НазваниеЗадача 1 определение опорных реакций балки
    АнкорРАсчетно графическая работа по Теоретической механике
    Дата07.05.2021
    Размер339.55 Kb.
    Формат файлаdocx
    Имя файлатеор мех РГР 1 вариант 20.docx
    ТипЗадача
    #202512

    Министерство образования Республики Беларусь

    Учреждение образования

    «Полоцкий государственный университет»


    Кафедра технологии и оборудования

    машиностроительного производства


    Расчетно-графическая работа
    По дисциплине «ТЕОРЕТИЧЕСКАЯ МЕХАНИКА»
    Раздел «СТАТИКА»

    Шелкунов Максим Андреевич

    группа 20 -- ТМ

    ВАРИАНТ №20

    Проверил: Старший преподаватель кафедры

    ТиОМП

    Тихон Елена Михайловна
    Новополоцк, 2021

    ЗАДАЧА 1.1
    ОПРЕДЕЛЕНИЕ ОПОРНЫХ РЕАКЦИЙ БАЛКИ

    Балка АВ, нагруженная произвольной плоской системой сил, удерживается в равновесии при помощи неподвижной шарнирной опоры А и подвижной шарнирной опоры С. Определить реакции опор, если


    F1 ,кН
    F2 ,кН
    М,кН×м
    q, кН/м
    α

    14
    4
    6
    6
    30⁰



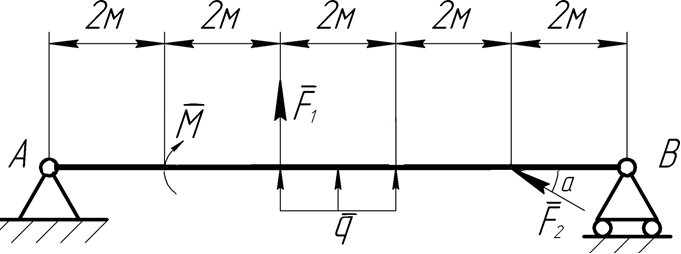    Решение.

    Для определения реакций опор рассмотрим равновесие балки АВ. Составим расчетную схему несвободной балки, находящейся в равновесии, заменяя опоры, возникающими в них силами реакций. Равномерно распределенную нагрузку интенсивностью q, заменим равнодействующей силой Q.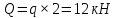



    Линия действия силы Q проходит через середину участка длиной 2 м, на котором эта нагрузка действует.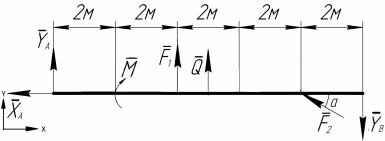



    Выбрав оси проекций Х и Y, составляем и решаем уравнения равновесия

    балки:

    Сумма проекций на ось X сил, действующих на балку, равна нулю,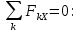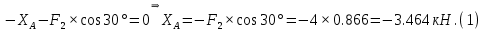





    Сумма проекций на ось Y сил, действующих на балку, равна нулю,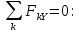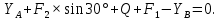



    (2)

    Сумма моментов всех сил относительно некоторого полюса равна нулю. За

    полюс примем опору А.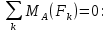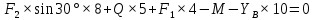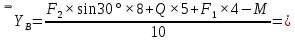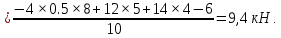









    Из уравнения (2)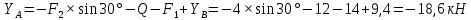

    .

    Ответ: , , .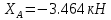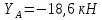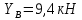

    Задача 1.3

    ОПРЕДЕЛЕНИЕ РЕАКЦИЙ ОПОР СОСТАВНОЙ БАЛКИ

    Определить реакции опор А и В составной конструкции, изображенной на рисунке и шарнирного соединения С.

    P1,

    кН
    P2,

    кН
    М,

    кН*м
    q,

    кН/м

    5
    12
    2
    3




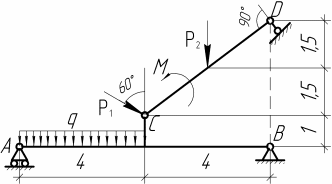    Решение. Разбиваем основную систему на две эквивалентные в месте их соединения шарниром С, заменяя связь уравновешивающимися парами сил. Равномерно распределенную нагрузку интенсивностью q, заменим равнодействующей силой Q.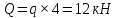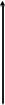



    X

    Y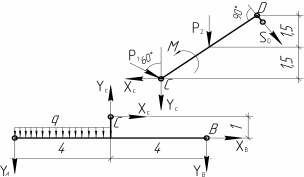


    Вычислим угол между осью OX и SD: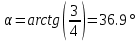



    Рассмотрим равновесие верхней части конструкции.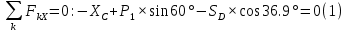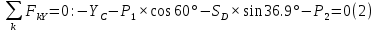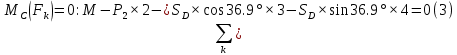







    Рассмотрим равновесие нижней части конструкции.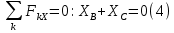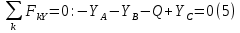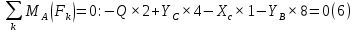







    Из 3-го уравнения выражаем :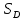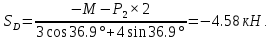



    Далее 1-го уравнений выражаем :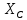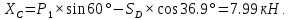



    Из 2-го уравнения выражаем :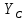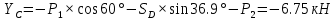



    Из 4-го уравнения выражаем :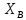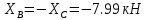



    Из 6-го уравнений выражаем :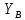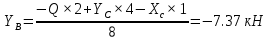



    Из 5-го уравнений выражаем :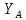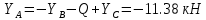


    Ответ: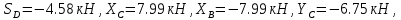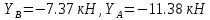

    .
    Задача 1.4.

    ПРИВЕДЕНИЕ СИСТЕМЫ СИЛ, НЕ ЛЕЖАЩИХ В ОДНОЙ ПЛОСКОСТИ, К ПРОСТЕЙШЕМУ ВИДУ
    Определитьглавныйвекториглавный моментзаданнойсистемысилотносительноцентраO.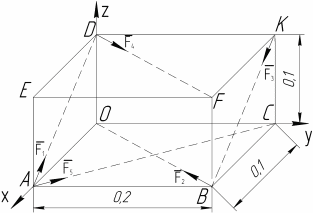



    a, м
    b, м
    c, м
    F1, Н
    F2, Н
    F3, Н
    F4, Н
    F5, Н

    0.1
    0.2
    0.1
    4
    8
    1
    15
    7

    Решение. Найдем необходимые углы: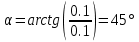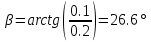



    Найдем главный вектор данной системы сил: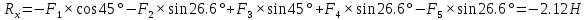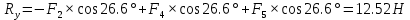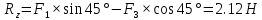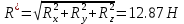









    Найдем главный момент данной системы сил: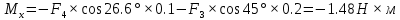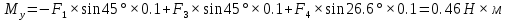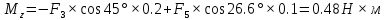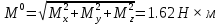









    Ответ: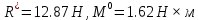

    написать администратору сайта