Задача 1 Определить величину и направление реакций связей для схем, приведенных на рис. Дано Q
 Скачать 293.37 Kb. Скачать 293.37 Kb.
|
|
Вариант 15 Задача № 1 Определить величину и направление реакций связей для схем, приведенных на рис. Дано: Q=13кН, α=450, β=400, схема - 10 Решение: Эта задача на равновесие плоской системы сходящихся сил. Для её решения необходимо выделить объект равновесия, т.е. тело или точку, где пересекаются линии действия всех сил. В нашем случае следует рассмотреть равновесие в точке A (рис.1). По условию задачи к данной точке прикладываем силу Q, с которой груз воздействует на объект равновесия, заменяя ее связь. Действие стержней АВ и АС заменяем их реакциями, и также прикладываем к точке А, предполагая, что стержни растянуты. 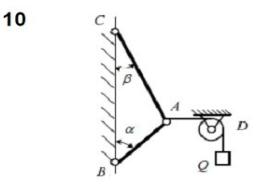 Рис.1 – Расчетная схема Освободившись от связей, переносим данные силы на координатную плоскость так, чтобы точка равновесия находилась в начале осей координат, и составляем уравнение равновесия плоской системы сходящихся сил относительно оси x и y через проекции её слагаемых на каждую из двух координатных осей (рис. 2). 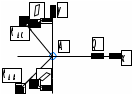 Рис.2 – Расчетная схема с реакциями Учитывая направление сил и угол наклона к каждой оси, составим уравнения проекций сил через уравнения равновесия плоской системы сходящихся сил: 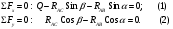 Решаем полученную систему 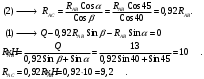 Усилия в стержнях АВ и АС от приложенной внешней силы получились соответственно 10 кН и 9,2 кН. То, что значения сил в стержнях получились со знаком «+», говорит о том, что мы угадали его направления. Задача № 2 Определить величину и направление реакций связей для схем, приведенных на рис. Дано: F1=24кН, F2=25кН, схема - 10 Решение: Эта задача на равновесие плоской системы сходящихся сил. Для её решения необходимо выделить объект равновесия, т.е. тело или точку, где пересекаются линии действия всех сил. В нашем случае следует рассмотреть равновесие в точке С (рис.1). По условию задачи к данной точке прикладываем силы F, с которой они воздействуют на объект равновесия. Действие стержней СА и СВ заменяем их реакциями, и также прикладываем к точке С, предполагая, что стержни растянуты. 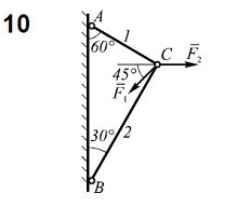 Рис.1 – Расчетная схема Освободившись от связей, переносим данные силы на координатную плоскость так, чтобы точка равновесия находилась в начале осей координат, и составляем уравнение равновесия плоской системы сходящихся сил относительно оси x и y через проекции её слагаемых на каждую из двух координатных осей (рис. 2).  Рис.2 – Расчетная схема с реакциями Учитывая направление сил и угол наклона к каждой оси, составим уравнения проекций сил через уравнения равновесия плоской системы сходящихся сил: 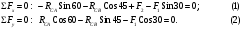 Решаем полученную систему 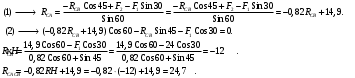 Усилия в стержнях СВ и СА от приложенной внешней силы получились соответственно -12кН и 24,7 кН. У сил, полученных со знаком «–» нужно поменять направление на противоположное, то есть стержень сжат. Задача № 3 Определить опорные реакции в балке Дано: F=24H, l=2,5м, схема - 15 Решение: В данной задаче будем рассматривать плоскую систему произвольно-расположенных сил. 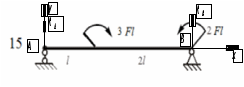 Рис.1 – Расчетная схема По условию задачи имеем одну шарнирно-подвижную опору и одну шарнирно-неподвижную. Условно покажем реакции опор, действующих на балку, на координатной плоскости (рис. 1), и составим систему уравнений моментов сил относительно опор, исходя из условия, что изгибающий момент численно равен алгебраической сумме моментов сил по одну сторону от рассматриваемого сечения, где момент относительно точки равен произведению силы на плечо действия этой силы по отношению к заданной точке: 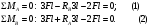 Если момент пытается повернуть балку относительно выбранной точки по часовой стрелке, то он берется со знаком «+», в обратном случае — со знаком «–». Решаем полученную систему 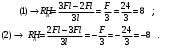 Значения, полученные со знаком «+», указывают что выбранные нами направления сил правильные. У сил, полученных со знаком «–» нужно поменять на противоположное. Теперь проведем проверку правильности решения по алгебраической сумме проекций всех внешних сил на ось перпендикулярную балке: 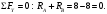 Реакции опор определены правильно. Задача № 4 В шарнирно-стержневой конструкции определить реакции в опоре и реакцию в стержне Дано: F=15H, l=3м, схема - 15 Решение: 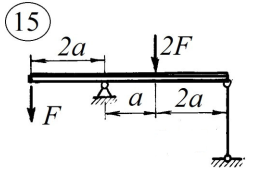 Рис.1 – Заданная схема Для решения задачи, покажем систему координат x-y и зададим произвольное направление реакций. 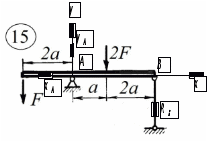 Рис. 2 – Расчетная схема В точке A реакция в опоре раскладывается на две составляющие — вертикальную xA и горизонтальную yA. Реакция в стержне RB всегда направлена вдоль самого стержня. Для определения трех реакций требуется три уравнения равновесия. Это будут два уравнения суммы моментов относительно точек в опорах и сумма проекций всех сил на ось x равные нулю. Составим их: 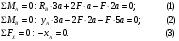 Из полученных уравнений выражаем и определяем искомые реакции опор  Выполним проверку найденных реакций, проецируя все силы на ось y. 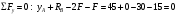 Равенство нулю суммы проекций всех сил и реакций показывает то, что реакции опор определены верно. Таким образом, заданная балка удерживается в равновесии под действием двух активных и трех реактивных сил. Задание № 5 Определить значение реакций в опорах Дано: F=25H, q=0,35Н/м, М=50Н/м, а=0,35м, b=1,2м, с=0,9м, схема – 15 Решение: В данной задаче будем рассматривать плоскую систему произвольно-расположенных сил. 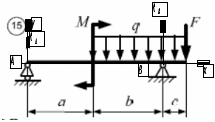 Рис.1 – Расчетная схема По условию задачи имеем одну шарнирно-подвижную опору и одну шарнирно-неподвижную. Условно покажем реакции опор, действующих на балку, на координатной плоскости (рис. 1), и составим систему уравнений моментов сил относительно опор, исходя из условия, что изгибающий момент численно равен алгебраической сумме моментов сил по одну сторону от рассматриваемого сечения, где момент относительно точки равен произведению силы на плечо действия этой силы по отношению к заданной точке: 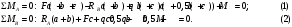 Если момент пытается повернуть балку относительно выбранной точки по часовой стрелке, то он берется со знаком «+», в обратном случае — со знаком «–». Решаем полученную систему 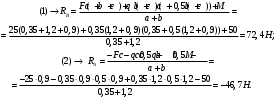 Значения, полученные со знаком «+», указывают что выбранные нами направления сил правильные. У сил, полученных со знаком «–» нужно поменять на противоположное. Теперь проведем проверку правильности решения по алгебраической сумме проекций всех внешних сил на ось перпендикулярную балке: 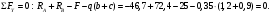 Реакции опор определены правильно. |
