задание. Задача 1 По предприятиям города имеются следующие данные за отчетный год предприятия
 Скачать 174.94 Kb.
|
|
Средняя прибыль: 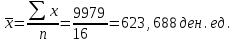 Дисперсия: 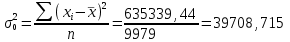 Так как число групп задано, определим величину интервалапо формуле: 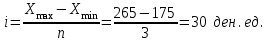 где Xmax, Хmin – максимальное и минимальное значение изучаемого признака; п – количество групп. Получим следующие интервалы: 1 группа: 175-205 ден.ед. 2 группа: 205-235 ден.ед. 3 группа: 235-265 ден.ед. Составим вспомогательную таблицу 2:
Получим группировку в таблице 3:
Межгрупповая дисперсия  измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних  от общей средней  . Показатель вычисляется по формуле , где  –групповые средние,  – общая средняя, –число единиц в j-ой группе, k – число групп.Для расчета межгрупповой дисперсии  построим вспомогательную таблицу. При этом используются групповые средние значения  из таблицы 3 (графа 4).Вспомогательная таблица 4 для расчета межгрупповой дисперсии:
Расчет межгрупповой дисперсии 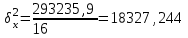 по формуле (11): Расчет эмпирического коэффициента детерминации 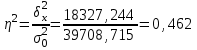 по формуле: или 46,2%Эмпирическое корреляционное отношение 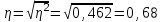 оценивает тесноту связи между факторным и результативным признаками и вычисляется по формуле: Значение показателя изменяются в пределах  . Чем ближе значение  к 1, тем теснее связь между признаками. Для качественной оценки тесноты связи на основе служит шкала Чэддока:Таблица 5 – Шкала Чэддока
46,2% вариации прибыли обусловлено вариацией вложений в уставные капиталы предприятий, а 53,8% – влиянием прочих неучтенных факторов. Согласно шкале Чэддока связь между признаками вложения в уставные капиталы предприятий и прибыль предприятий является заметной. Задача № 14 По группе промышленных предприятий имеются следующие данные:
Определить общую дисперсию объема продукции. Решение: Средний объем продукции определим по формуле средней арифметической взвешенной: 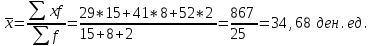 Определим межгрупповую дисперсию по формуле: 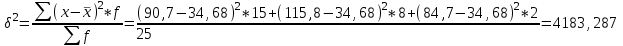 Средняя из внутригрупповых дисперсий – это средняя арифметическая взвешенная из дисперсий групповых: 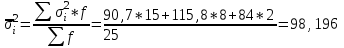 Общая дисперсия: 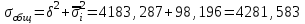 Задача № 32 Численность населения области характеризуется следующими данными (тыс. чел): 1. На начало года а) постоянное население 640 в т.ч. временно отсутствующие 40 б) временно проживающие 30 В течение года: а) родилось 8,1 в т.ч. постоянного населения 6,9 б) умерло 3,1 в т.ч. постоянного населения 2,5 в) прибыло на постоянное место жительства 17,0 г) возвратилось временно отсутствующих 35,0 д) выбыло из постоянного населения на постоянное жительство в другие населенные пункты 7,1 Определите: а) численность наличного населения области на начало и конец года; б) численность постоянного населения области на конец года; в) для постоянного населения коэффициенты, характеризующие естественное движение населения и его миграцию. Решение: а) Численность наличного населения на начало года найдём по формуле: 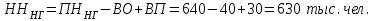 Численность наличного населения на конец года найдём по балансовой схеме: 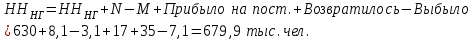 б)Численность постоянного населения области на конец года: 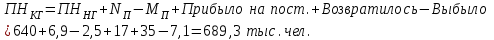 в)Среднегодовую численность постоянного населения найдем по формуле: 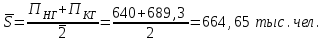 Коэффициент рождаемости: 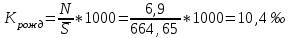 Коэффициент смертности: 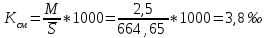 Коэффициент естественного прироста населения:  Коэффициент механического прироста населения: 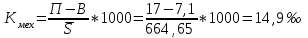 Коэффициент общего прироста населения: 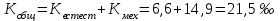 На 1000 человек населения приходится 10 чел родившихся. Число умерших за год в расчете на 1000 человек населения составило 4 человек. Наблюдается естественный прирост населения – 6 человек. Задача № 38 Имеются данные о списочной численности работников предприятия за март:
Определите: 1. Среднесписочную численность работников, среднеявочную, среднее число фактически работавших; 2. Коэффициенты использования среднесписочного числа и среднеявочного числа работников. Решение: Среднюю списочную численность работников за месяц определим путём деления суммы численности работников списочного состава за все календарные дни месяца на число календарных дней ( | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
в группе
