задание. Задача 1 По предприятиям города имеются следующие данные за отчетный год предприятия
 Скачать 174.94 Kb. Скачать 174.94 Kb.
|
|
Задача № 1 По предприятиям города имеются следующие данные за отчетный год:
Сгруппируйте предприятия по объему продукции, выделив три группы с равными интервалами. По каждой группе определить: - число предприятий; - в целом и в среднем на одно предприятие: объем продукции, фонд заработной платы; - размер заработной платы на 1 ден. ед. объема продукции. Решение оформить в виде статистической таблицы. Сформулировать вывод. Решение: Так как число групп задано, определим величину интервалапо формуле: 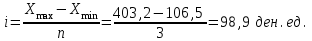 где Xmax, Хmin – максимальное и минимальное значение изучаемого признака; п – количество групп. Получим следующие интервалы: 1 группа: 106,5-205,4 ден.ед. 2 группа: 205,4-304,3 ден.ед. 3 группа: 304,3-403,2 ден.ед. Составим вспомогательную таблицу:
Составим итоговую группировку:
Расчеты показали, что наблюдается тенденция уменьшения количества предприятий при увеличении объема продаж, фонд заработной платы на одно предприятие увеличивается, при этом средняя заработная плата на 1 ден.ед. продукции уменьшается. Также группировка показывает прямую зависимость между объемом продажи и фондом заработной платы. Рост объема продаж приводит к увеличению фонда заработной платы. Задача № 4 За отчетный год потребление топлива на производственные нужды составило:
Определить: 1. Процент выполнения плана по общему расходу топлива, если коэффициенты пересчета в условное топливо следующие: уголь – 0,9 ; нефть - 1,3; газ – 1,2. 2. Долю фактически израсходованного каждого вида топлива в общем объеме потребления. Для определения общего потребления топлива используется условно-натуральный метод. Расходы по плану и фактически исчисляются в единицах условного топлива: 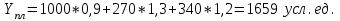 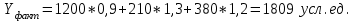 Процент выполнения плана по общему расходу топлива: 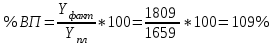
Фактический расход топлива превышает плановый на 9%. Наибольшую долю израсходованного топлива в общем объеме топлива занимает уголь – 59,7%, а наименьшую нефть – 15,1%. На долю расхода газа приходится 25,2%. Задача № 6 Численность экономически активного населения и безработных в двух регионах (в среднем за год) составили:
Определить относительные величины интенсивности и относительные величины, характеризующие изменение доли численности безработных в общей численности экономически активного населения. С помощью относительных величин дать сравнительную оценку безработицы в двух регионах. Решение: Показатель интенсивности – это отношение значений двух разнородных абсолютных величин для одного периода времени и одной территории или объекта: Рассчитаем коэффициенты занятости и безработицы в каждом регионе в каждом году по формулам: Коэффициент безработицы: 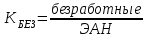 Коэффициент занятости населения: 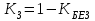 По 1 региону: 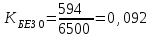 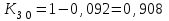 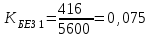 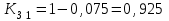 По 2 региону: 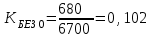 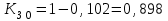 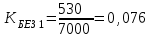 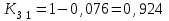 Определим изменение удельного вес численности безработных в общей численности экономически активного населения: По 1 региону: 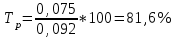 По 2 региону: 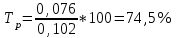 Относительная величина сравнения: 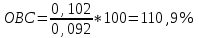 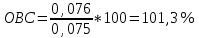 Во втором году по сравнению с первым коэффициент безработицы по 1 региону сократился на 18,4%, а по 2-му региону – 25,5%. Если провести сравнительную оценку безработицы двух регионов, то во втором регионе в 1-м году коэффициент безработицы был выше, чем в первом регионе на 10,9%, а во втором году на 1,3%. Положительным моментом является снижение безработицы во 2-м году по сравнению с 1-м годом в каждом регионе. Задача № 8 Имеется следующее распределение населения России по возрастным группам:
Рассчитать средний возраст населения России обычным способом и по способу моментов, моду и медиану, показатели вариации. Решение: Составим вспомогательную таблицу:
Средний возраст населения России определим по формуле средней арифметической взвешенной: 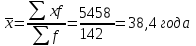 Дисперсия – это средний квадрат отклонений вариантов от их средней величины: 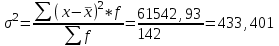 Среднее квадратическое отклонение равно корню квадратическому из дисперсии: 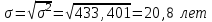 Коэффициент вариации: 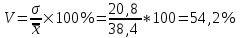 . .Значение моды для интервального ряда рассчитывается по формуле: Mo = XMo + h где XMo – нижнее значение модального интервала; mMo – число наблюдений; mMo-1 – то же для интервала, предшествующего модальному; mMo+1 – то же для интервала, следующего за модальным; h – величина интервала изменения признака в группах. Модальный интервал (20-30) – определяем по наибольшей частоте. 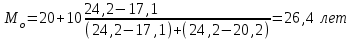 Медиана для интервального ряда: Me = XMe + hMe ∙ 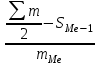 где ХМе – нижняя граница медианного интервала; hMe – его величина; Ʃm/2 – половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном и относительном выражении); SMe-1 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; mMe – число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо относительном выражении). Медианным является интервал 30-40, т.к. в этом интервале накопленная частота S, превышает половину общей суммы частот, в данном случае больше 71). 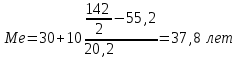 «Способ моментов» основан на математических свойствах дисперсии. Для рядов распределения с равными интервалами расчет дисперсии можно произвести по следующей формуле: 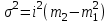 где i – размер интервала; m1 – момент первого порядка 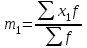 (х1 – упрощенные варианты; 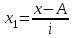 ); );m2 – момент второго порядка 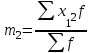 i=10 А=25 Построим вспомогательную таблицу:
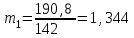 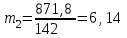 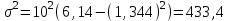 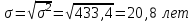 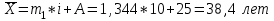 Средний возраст населения России составил 38,4 года. Чаще всего встречающийся возраст населения России составил 26,4 лет. Половина населения России старше 37,8 лет, а половина моложе 37,8 лет. . Каждое значение ряда отличается от среднего значения на 20,8 лет. Поскольку коэффициент вариации меньше 70%, но больше 30%, то вариация умеренная. Задача № 13 Имеются следующие данные по группе банков региона:
Для оценки влияния на прибыль банков суммы вложений в уставные капиталы других предприятий требуется: 1. Определить дисперсию прибыли банков региона; 2. Сгруппировать банки по сумме вложений в уставные капиталы других предприятий, выделив три группы, и исчислить: - для каждой группы внутригрупповую дисперсию прибыли; - межгрупповую и среднюю из внутригрупповых дисперсий прибыли; - долю средней из внутригрупповых дисперсий в общей дисперсии; 3. Сделать выводы. Решение: Составим вспомогательную таблицу 1:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||