математическое моделирование. Задача 1 Полигон с четырьмя станциями А, Б, в и г должен пропустить суточные объемы вагонопотоков N
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
Задача 1Полигон с четырьмя станциями А, Б, В и Г должен пропустить суточные объемы вагонопотоков NАГ и NБГ по заданному назначению в соответствии с нормативными показателями работы сортировочных парков на станциях А, Б и В. Требуется: 1. Составить план формирования поездов. 2. Выполнить вероятностный анализ плана и рассмотреть возможные его варианты с учетом случайного характера суточных объемов вагонопотоков NАГ и NБГ. Таблица 1 – Исходные данные
Решение Согласно условию, определяем критические значения вагонопотоков NАГ и NБГ:   Вывод: если N1 > N1кр = 190, то вагонопоток N1 пропускаем сквозным назначением до станции Г, минуя попутные технические станции Б и В; если N1 < 190, то N1 подлежит переработке на станциях Б и В. Аналогично, для потока N2: N2 > N2кр = 284, то N2 пропускается до станции Г сквозным назначением, минуя станцию В; при N2 < 284 поток N2 проходит переработку на станции В. 2. Устанавливаем всевозможные варианты плана формирования поездов, соответствующие следующим случайным событиям: А1: N1 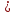 190, N2 > 284 вариант 1, 190, N2 > 284 вариант 1,А2: N1 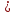 190, N2 < 284 вариант 2, 190, N2 < 284 вариант 2,А3: N1 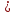 190, N2 > 284 вариант 3, 190, N2 > 284 вариант 3,А4: N1 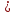 190, N2 < 284 вариант 4. 190, N2 < 284 вариант 4.3. Каждое из событий А1, А2, А3 и А4 равносильно одновременному наблюдению соответствующих двух независимых событий. Поэтому на основании теоремы умножения вероятностей независимых событий получаем: Р(А1) = Р(N1 > 190, N2 > 284) = P(N1 > 190) × P(N2 > 284), Р(А2) = Р(N1 > 190, N2 < 284) = P(N1 > 190) × P( N2 < 284), Р(А3) = Р(N1 < 190, N2 > 284) = P(N1 < 190) × P(N2 > 284), Р(А4) = Р(N1 < 190, N2 < 284) = P(N1 < 190) × P(N2 < 284). 4. Определяем вероятность реализации вариантов 1, 2, 3, 4 плана формирования поездов, как вероятности случайных событий А1, А2, А3, А4 согласно заданным законам распределения вероятностей вагонопотоков N1 и N2. Согласно нормальному закону распределения: Р(N1 190) = 1 – Р(N1 190) = 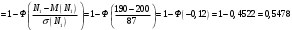 где Ф(x) – функция распределения стандартной нормальной случайной величины 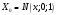 (функция Лапласа): (функция Лапласа): Значение функции Ф(х) взято в приложении 2 [Карпухин, В. Б. Теория и практика математического моделирования в задачах транспортной системы : учебное пособие / В. Б. Карпухин ; М-во транспорта Рос. Федерации, Рос. ун-т транспорта (МИИТ), Рос. Открытая акад. транспорта. – Москва : РУТ (МИИТ): РОАТ, 2021. – 111 с.]. В расчете вероятности Р(NАГ > 190) использована теорема сложения вероятностей противоположных событий: Р(Х > х) + Р(Х < х) = 1. Аналогично получаем вероятность выделения потока N2 в сквозное назначение при N2 > 284: Р(N2 284) = 1 – Р(N2 284) = 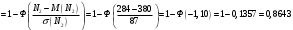 Замечание: при вероятностном анализе вагонопотоков кроме нормального закона распределения вероятностей, описываемого функцией Лапласа Ф(x), рассматриваются также законы показательного, Эрланга 2-, 3- и 4-го порядков и равномерного распределений. Используя полученные результаты, определяем: Р(А1) = Р(N1 > 190, N2 > 284) = 0,5478 0,8643 = 0,4735 P(А2) = P(N1 > 190, N2 < 284) = 0,5478 (1 – 0,8643) = 0,0743 P(А3) = P(N1 < 190, N2 > 284) = (1 – 0,5478) 0,8643 = 0,3908 P(А4) = P(N1 < 190, N2 < 284) = (1 – 0,5478) (1 – 0,8643) = 0,0614 5. События А1, А2, А3, А4 являются несовместными и составляют полную систему событий. На основании теоремы о вероятности суммы событий, составляющих полную систему, при суммировании вероятностей событий А1, А2, А3, А4 должна получится единица: Р(А1 + А2 + А3 + А4) = Р(А1) + Р(А2) + Р(А3) + Р(А4) = 0,4735 + 0,0743 + 0,3908 + 0,0614 = 1,0000 Полученный результат свидетельствует о правильности выполненного вероятностного анализа плана формирования поездов в соответствии с исходными данными. 6. Вариант 4, соответствующий событию А4, предусматривает организацию вагонопотока N1 через станции Б и В и вагонопотока N2 через станцию В c переработкой, без сквозного назначения. Однако в силу случайного характера вагонопотоков N1 и N2 их величины могут быть таковыми, что возможны два несовместных подварианта варианта 4: 4а: N1 + N2 < N2кр, N1 < N1кр, N2 < N2кр, 4б: N1 + N2 > N2кр, N1 < N1кр, N2 < N2кр, Если имеет место подвариант 4б, то открывается возможность сформировать на станции Б суммарный вагонопоток N1 + N2 > N2кр, который проходит сквозным назначением через попутную станцию В до станции Г. 7. Определяем вероятности Р(4а) и Р(4б) подвариантов 4а и 4б. 7.1. Согласно анализу события А4 с помощью рис. 1 имеем два случая. Случай 1: N1кр < N2кр. 1) Событие А4 равносильно наблюдению точки M(N1, N2) с координатами N1 < N1кр, N2 < N2кр в площади четырехугольника ON2кр M0 N1кр. 2) Прямая N1 + N2 = N2кр делит прямоугольник ON2кр M0 N1кр на две части: - трапецию ON2кр M2 N1кр, точки которой имеют координаты N1 < N1кр, N2 < N2кр, N1 + N2 < N2кр, что соответствует подварианту 4а; - треугольник N2кр M0 M2, точки которого также с координатами N1 < N1кр, N2 < N2кр, но N1 + N2 > N2кр, что соответствует подварианту 4б. 3) Для определения вероятности P(4а) используем тот же метод, который применили для определения вероятности P(А4), перемножая P(N1 < N1кр) на P(N2 < N2кр). С этой целью: а) Разобьём трапецию ON2крM2N1кр на несколько частичных трапеций (рис. 1). Чем их больше, тем точнее выразим вероятность наблюдения точки M(N1, N2) с координатами N1 < N1кр, N2 < N2кр, N1 + N2 < N2кр через сумму вероятностей их наблюдения в площадях частичных трапеций. На рис. 1 трапеция ON2кр M2 N1кр разбита на три частичные трапеции (минимальное рекомендуемое число). б) Частичные трапеции заменим равными по площади прямоугольниками - OM3 M4 M5 с основанием 0 N1 50, высотой 0 N2 259, 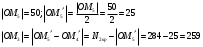 - M5 M6 M7 M8 с основанием 50 N1 100, высотой 0 N2 209, 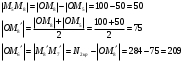 - M8 M9 M10 N1кр с основанием 100 N1 190, высотой 0 N2 139,  в) используя заданные (оба нормальные) законы распределения вероятностей вагонопотоков N1 и N2, по формуле  находим вероятности наблюдения точки M(N1, N2) с координатами N1 < N1кр, N2 < N2кр, N1 + N2 < N2кр в площадях прямоугольников OM3 M4 M5: P1(0 N1 50, 0 N2 259) = P(0 N1 50).   (0,0427 – 0,0107) (0,0823 – 0,0000) = 0,0026 (0,0427 – 0,0107) (0,0823 – 0,0000) = 0,0026M5 M6 M7 M8: P2(50 N1 100, 0 N2 209) = P(50 N1 100). 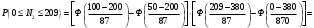  (0,1215 – 0,0427) (0,0244 – 0,0000) = 0,0019 (0,1215 – 0,0427) (0,0244 – 0,0000) = 0,0019M8 M9 M10 N1кр: 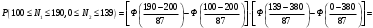  (0,4522 – 0,1251) (0,0026 – 0,0000) = 0,0009 (0,4522 – 0,1251) (0,0026 – 0,0000) = 0,0009г) Вероятность подварианта 4а равна P(4а) = P1 + P2 + P3 = 0,0026 + 0,0019 + 0,0009 = 0,0054 4) Вероятность P(4б) определяем либо по аналогии с определением вероятности P(4а), разбивая треугольник N2кр M0 M2 на частичные трапеции и треугольник и заменяя их равными по площади прямоугольниками, либо по теореме о вероятности суммы несовместных событий, поскольку события 4а и 4б несовместны. Имея по теореме P(4а) + P(4б) = P(A4), получим P(4б) = P(A4) – P(4а) = 0,0614 – 0,0054 = 0,0560 7.2. Случай 2: N1кр > N2кр. На рис. 1 вариант 4 соответствует наблюдению точки M(N1, N2), N1 < N1кр, N2 < N2кр в площади прямоугольника ON2крM1N1кр, подвариант 4а соответствует наблюдению точки M(N1, N2), N1 < N1кр, N2 < N2кр, N1 + N2 < N2кр в площади треугольника ON2кр (N2кр = N1), подвариант 4б соответствует наблюдения точки N1 < N1кр, N2 < N2кр, N1 + N2 > N2кр в площади трапеции (N2кр = N1) N2крM1N1кр. Вероятности варианта 4 и подвариантов 4а и 4б определяют по аналогии случая 1. 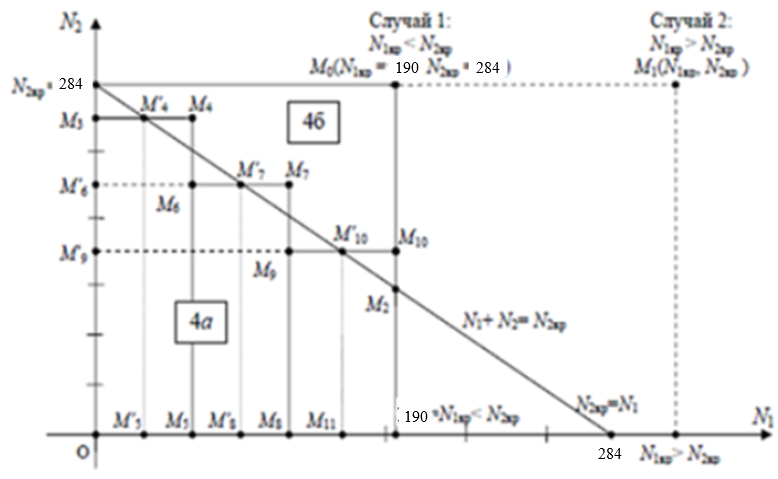 Рис. 1. Вариант 4, подварианты 4а и 4б 8. Схема полигона АГ и варианты плана формирования поездов представлены на рис. 2.  Рис. 2. Полигон АГ и варианты плана формирования поездов. ЗАДАЧА 2 На станции отправления формируются вагонопотоки на 2 назначения А и Б. Определить оптимальный ежесуточный объем вагонопотоков, обеспечивающий РЖД максимальную прибыль при доставке грузов к станциям назначения, если формирование осуществляется с помощью 3 технологических операций: 1) осмотр 1 вагона назначения А требует t11 – 0,15 часа, назначения Б t12 – 0,4 часа, 2) формирование 1 вагона в вагонопоток назначения А t21 – 0,23 часа, назначения Б t22 – 0,34 часа, 3) погрузка 1 вагона назначения А t31 – 0,4 часа, назначения Б t32 – 0,16 часа. Прибыль от доставки груза 1 вагоном на станцию назначения А составляет с1 – 10, на станцию назначения Б с2 – 12 денежных единиц. вагонопоток х1 = 46, х2 = 35 прибыль назначения СА = 460, СБ = 420 общая прибыль на РЖД С = 880 РЕШЕНИЕ 1.Математическая модель стандартного вида для данной задачи. Суммарная прибыль 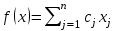 (2.1) (2.1)Общее время проведения i-ой технологической операции 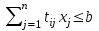 (2.2) (2.2)где b – заданное время формирования объема вогонопотоков, b= 24часа Максимальное значение целевой функции  (2.3) (2.3)Запишем уравнения математической модели для конкретной задачи согласно уравнениям (2.1), (2.2), (2.3). 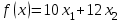 (2.4) (2.4) (2.5) (2.5) (2.6) (2.6)2. Введем балансовые переменные  . Обращая неравенства (2.5) в равенства . Обращая неравенства (2.5) в равенства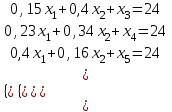 (2.7) (2.7)На множестве неотрицательных решений системы уравнений (2.7) необходимо найти максимальное значение линейной функции (2.4). 3. Исследуем систему (2.7) на совместимость. Поскольку ранг матрицы А и расширенной матрицы А|B равны и меньше числа переменных n=5  то в соответствии с теоремой Кронекера-Капелли систему (2.7) является совместной и неопределенной, базисных переменных 3, свободных 2. 4. Для поиска оптимального решения симплексным методом представим выражения (2.4) и (2.7) в базисной допустимой форме согласно условиям: 1) в каждом из выражений (2.7) должна входить только одна базисная переменная с коэффициентом 1; 2) свободные члены системы уравнений (2.7) должны быть неотрицательными; 3) целевая функция (2.4) должна быть выражена только через свободные переменные. В качестве базисных переменных принимаем переменные  , а свободных - , а свободных - 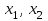 , тогда выражения (2.4) и (2.7) соответствуют условия базисной допустимой формы и позволяют получить 1-е базисное допустимое решение поставленной задачи при равенстве нулю свободных переменных: , тогда выражения (2.4) и (2.7) соответствуют условия базисной допустимой формы и позволяют получить 1-е базисное допустимое решение поставленной задачи при равенстве нулю свободных переменных: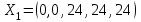 (2.8) (2.8) (2.9) (2.9)Решение (2.8) и (2.9) – опорное. 5. Перейдем к новой базисной допустимой форму и получим на её основе новое базисное допустимое решение 1) в системе (2.7) выразим базисные переменные через свободные переменные  (2.10) 2) пусть 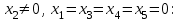  тогда min(60; 70,59; 150) = 60 = Х2min при х3 = 0. Получаем новые свободные переменные х1 = 0 и х3 = 0 и новые базисные переменные    . .3) Из уравнения (2.10в) выразим х2через х1 и х3  и подставим в (2.10б), (2.10а) и (2.4) 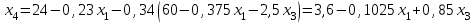   получим новую базисную форму 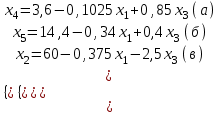 (2.11) (2.11) (2.12) (2.12)4) из уравнения (2.11) и (2.12) получим 2 е базисное решение при х2 = 0 и х5 = 0 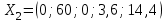 (2.13) (2.13) (2.14) (2.14)Вывод: из (2.12) видно, что при увеличении  целевая функция увеличивается, при увеличении целевая функция увеличивается, при увеличении 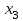 – уменьшается, поэтому принимаем – уменьшается, поэтому принимаем 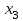 =0, =0,  0 и находим допустимое значение 0 и находим допустимое значение  . .6. От базисной допустимой формы (2.11), (2.12) перейдем к новой базисной форме 1) пусть  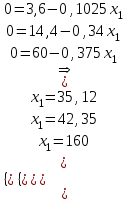 тогда min(160; 35,12; 42,35) = 35,12 = Х1min при х4 = 0. Получаем новые свободные переменные х3 = 0 и х4 = 0 и новые базисные переменные 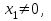  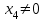 . .3) Из уравнения (2.11а) выразим х1 через х3 и х4   и подставим в (2.11б), (2.11в) и (2.12)  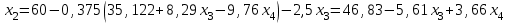  получим новую базисную форму  (2.14) (2.14) (2.15) (2.15)4) из уравнения (2.14) и (2.15) получим 3 е базисное решение при х3 = 0 и х5 = 0  (2.16) (2.16) (2.17) (2.17)Вывод: из (2.15) видно, что при увеличении х3 и х5 уменьшается  . Симплекс процесс завершен. . Симплекс процесс завершен.Графическое решение задачи представлено на рис. 2.1.  Рис. 1.1. Графическое решение задачи |
