математическое моделирование. Задача 1 Полигон с четырьмя станциями А, Б, в и г должен пропустить суточные объемы вагонопотоков N
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
ЗАДАЧА 4 Задана матрица транспортной сети G(X,U,C(U)). Построить диаграмму и найти максимальный поток и минимальный разрез. Исходные данные:
РЕШЕНИЕ Транспортная сеть – сеть, характеризуемая следующими признаками: 1) имеет только одну вершину входа, называемую источником, 2) имеет только одну вершину выхода, называемую стоком, 3) Каждой дуге uj 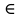 U соответствует некоторое неотрицательное целое число с(uj) ≥ 0, с(uj) U соответствует некоторое неотрицательное целое число с(uj) ≥ 0, с(uj)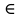 С(U), называемое пропускной способностью дуги. С(U), называемое пропускной способностью дуги.Транспортная сеть является связанным графом без контуров и петель. Связанный граф – граф, в котором для любых двух его вершин существует маршрут (путь), соединяющий эти вершины. Задача определения максимального потока является одной из основных при анализе и синтезе транспортной сети, решается с помощью понятия «разрез сети » на основе теоремы Форда-Фалкерсона: в любой транспортной сети величина максимального потока от источника к стоку равна пропускной способности минимального разреза. Ориентированным разрезом транспортной сети G(X,U,C(U)) называется множество дуг 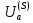 c началом в подмножестве вершин А и с концом в подмножестве вершин В c началом в подмножестве вершин А и с концом в подмножестве вершин ВПропускной способностью или величиной разреза С( 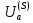 ) называется сумма пропускных способностей дуг ) называется сумма пропускных способностей дуг  разреза транспортной сети. разреза транспортной сети.Построим граф транспортной сети в соответствии с заданной матрицей (рис. 3.1). 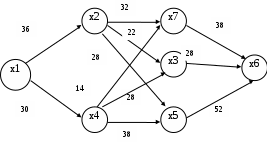 Рис. 3.1. Граф транспортной сети По графу составим возможные пути от вершины входа к вершине выхода S1 = [(х1;х2)36; (х2,х7)32] S2 = [(х1;х2)36; (х2;х3)22; (х3;х6)28; (х6;х7)38] S3 = [(х1;х2)36; (х2;х5)28; (х5;х6)52; (х6;х7)38] S4 = [(х1;х4)30; (х4;х7)14] S5 = [(х1;х4)30; (х4;х3)28; (х3;х6)28; (х6;х7)38] S6 = [(х1;х4)30; (х4;х5)38; (х5;х6)52; (х6;х7)38] Находим максимальный поток и минимальный разрез с помощью алгоритма Форда-Фалкерсона. Составим матрицу С пропускной способности дуг заданной транспортной системы (Таблица 3.1). Таблица 3.1. Матрица С
Рассмотрим путь S1. Пропускная способность пути S1. P1 = min(36;32)=32. В матрице С из значений дуг пути S1 вычтем Р1=32 получив матрицу С1 (Таблица 3.2). Таблица 3.2. Матрица С1
Рассмотрим путь S2(C1)= [(1;2)4; (2;3)22; (3;6)28; (6;7)38]. P2(C1)=min(4;22;28;38)=4. Преобразуем матрицу С1 в С2 вычтя P2=4 из значений дуг пути S2(C1). Таблица 3.3. Матрица С2
Рассмотрим путь S4(C2)= [(1;4)30; (4;7)14]. P3(C2)=min(30;14)=14. Преобразуем матрицу С2 в С3 вычтя P3=14 из значений дуг пути S3(C2). Таблица 3.4. Матрица С3
Рассмотрим путь S5(C3)= [(1;4)16; (4;3)28; (3;6)24; (6;7)34]. P4(C3)=min(16;28;24;34)=16. Преобразуем матрицу С3 в С4 вычтя P4=16 из значений дуг пути S4(C3). Таблица 3.5. Матрица С4
Элементы первой строки равны нулю, процесс завершен. Максимально возможный поток Pmax = P1+P2 + P3+P4 = 32+4+14+16=66. Вычтем из элементов матрицы С элементы матрицы С4 получив матрицу С5. Таблица 3.6. Матрица С5
Построим граф варианта движения, реализующего величину максимального потока (Рис.3.2). 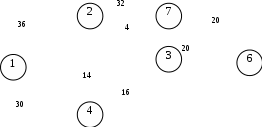 Рис. 3.2. Граф варианта движения, реализующего величину максимального потока 4. Рассмотрим всевозможные разрезы на графе варианта движения и убедимся в том, что согласно теореме Форда-Фалкерсона величина максимального потока от источника к источнику равна пропускной способности минимального разреза транспортной сети с17=43. Поток в транспортной сети удовлетворяет требуемый условиям: 1) для любой дуги значение потока не превышает пропускной способности, 2) в каждой вершине соблюдается условие непрерывности потока. В 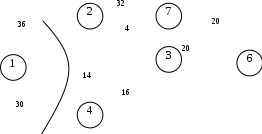 еличина разреза: 36+30=66. еличина разреза: 36+30=66.Рис. 3.3. Минимальный разрез 5. Проверим результаты расчета, выбрав другой путь: S6 = [(х1;х4)30; (х4;х5)38; (х5;х6)52; (х6;х7)38] Р’1=min(30;38;52;38)=30 Преобразуем матрицу С в С’1 Таблица 3.8. Матрица С’1
Рассмотрим путь S3 (C’1)= [(х1;х2)36; (х2;х5)28; (х5;х6)22; (х6;х7)8]. P’2(C’1)=min(36;28;22;8)=8. Преобразуем матрицу С’1 в С’2 вычтя P’2=8 из значений дуг пути S3(C’1). Таблица 3.9. Матрица С’2
Рассмотрим путь S1(C’2)= [(х1;х2)28; (х2,х7)32]. P’3(C2)=min(28;32)=28. Преобразуем матрицу С’2 в С’3 вычтя P’3=28 из значений дуг пути S’1(C’2). Таблица 3.10. Матрица С’3
Остальные пути пройти невозможно. Решение найдено. Максимально возможный поток Pmax = P’1+P’2 + P’3= 30+8+28=66. Вычтем из элементов матрицы С элементы матрицы С’3 получив матрицу С’4. Таблица 3.9. Матрица С’4
Вывод: Результаты расчета совпали с величинами максимального потока и минимального разреза при выполнении условия сохранения потока в промежуточных вершинах. ЗАДАЧА 5 В депо по ремонту вагонов работает n=2 бригад. В среднем в течение дня поступает в ремонт λ=10 вагонов и при семичасовом рабочем дне каждая из бригад ремонтирует µ=2,5 вагонов. Рассматривая депо как систему массового обслуживания, требуется: 1. Проверить исходные данные на адекватность условиям применения математической модели системы массового обслуживания. 2. В случае неадекватности принять решение по управлению параметрами работы депо с целью приведения в соответствие с условиями применения описывающей математической модели, а именно, выбрать необходимый уровень значений n, λ, µ. 3. Рассчитать характеристики эффективности 1) среднее время ремонта 1-го вагона, 2) среднее время ожидания начала ремонта для каждого вагона, 3) среднюю длину очереди. РЕШЕНИЕ 1. Проверим исходные данные на адекватность условиям математической модели системы массового обслуживания. Имеем СМО с неограниченной очередью. По условию: λ = 10 (ваг/смену), μ = 2,5, n = 2. 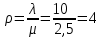 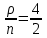 >1, следовательно, очередь будет расти до бесконечности. >1, следовательно, очередь будет расти до бесконечности.Исходные данные не адекватны условиям модели СМО. В этом случае необходимо принять решение по управлению системой массового обслуживания, т.е. назначить такие значения параметров 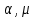 и n, которые обеспечивают необходимые условия применения математической модели. и n, которые обеспечивают необходимые условия применения математической модели.2. Примем решение по управлению параметрами работы депо с целью приведения в соответствии с условиями применения описывающее матмодель, а именно, увеличим число ремонтных бригад с 2-х до 5-ти. Получим новые исходные данные: n=5, =10, =2,5 тогда 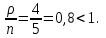 3. Рассчитаем характеристики интенсивности. 3.1) среднее время ремонта 1-го вагона. 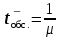 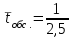 =0,4 рабочего дня или =0,4 рабочего дня или 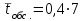 =2,8 час. =2,8 час.3.2) среднюю длину очереди. 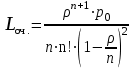 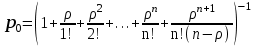 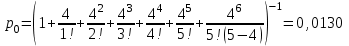 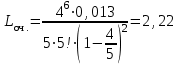 вагона вагона3.3) среднее время ожидания начала ремонта для каждого вагона. 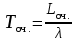 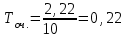 рабочего дня или рабочего дня или 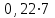 =1,55 час. =1,55 час.Ответ: 1) Среднее время ремонта одного вагона равно 2 часа 48 минут; 2) Среднее время ожидания начала ремонта для каждого вагона равно 1 час 33 минуты; 3) Средняя длина очереди равна 2,22 вагона. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
