математическое моделирование. Задача 1 Полигон с четырьмя станциями А, Б, в и г должен пропустить суточные объемы вагонопотоков N
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Ответ: при объеме суточного вагонопотока 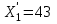 , включенного в назначение А, и , включенного в назначение А, и 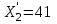 вагонов, включенного в назначение Б, РЖД получит максимальную прибыль вагонов, включенного в назначение Б, РЖД получит максимальную прибыль 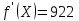 денежных единиц. денежных единиц.ЗАДАЧА 3 Имеются три пункта отправления однородного груза и пять пунктов его назначения. На пунктах отправления груз находится в количестве 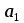 = 70, = 70, 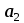 = 50, = 50, 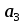 = 90 в пункты назначения требуется доставить соответственно = 90 в пункты назначения требуется доставить соответственно 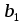 =10, =10,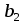 = 40, = 40, 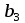 = 70, = 70, 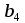 = 20, = 20, 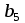 = 70 груза. Известна стоимость перевозки единицы груза из каждого пункта отправления в каждый пункт назначения (матрица D). = 70 груза. Известна стоимость перевозки единицы груза из каждого пункта отправления в каждый пункт назначения (матрица D). D = 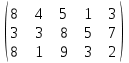 Найти такой план перевозок, при котором необходимо вывезти все запасы груза, полностью удовлетворить все потребности и обеспечить при этом минимум общих затрат на перевозку. Задачу решить методом потенциалов. РЕШЕНИЕ Проверим необходимое и достаточное условие разрешимости задачи 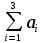 = = 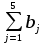 a1+a2+a=70+50+90=210 b1+b2+b3+b4+b5=10+40+70+20+70=210 Условия баланса соблюдены. Транспортная задача закрытого типа, т.к. 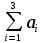 = = 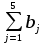 = 210. = 210.Составим распределительную таблицу.
Первоначальное распределение поставок составим, используя метод «наименьших затрат». На каждом шаге делаем поставку в клетку с наименьшей стоимостью перевозки единицы груза среди всех неотмеченных клеток. В ячейку (1,4) с минимальной стоимостью 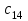 =1 назначим min(70, 20)=20. Четвертый столбец выходит из рассмотрения. =1 назначим min(70, 20)=20. Четвертый столбец выходит из рассмотрения.В оставшейся части в ячейку (3, 2) назначим min(90,40)=40. Второй столбец выходит из рассмотрения. В ячейку (3,5) назначим min(70, 90-40)=50. Третья строка выходит из рассмотрения. В ячейку (2,3) назначим min(70,70-20)=50. Третий столбец выходит из рассмотрения. В ячейку (1,5) назначим min(70-50,70-20)=20. Пятый столбец выходит из рассмотрения. В ячейку (2,1) назначим min(10,50)=10. Первый столбец выходит из рассмотрения. В ячейку (1,3) назначим min(70-20-20,70)=30. Первая строка выходит из рассмотрения. В ячейку (2,3) назначим min(50-10,70-30)=40.
Проверим полученный опорный план на невырожденность. Количество заполненных клеток N должно удовлетворять условию N=n+m-1 . В нашем случае количество занятых клеток 7=j+i-1=3+5-1=7, значит опорный план невырожденный. Перемножим числа стоящие в одной клетке (для всех клеток) затем полученные произведения сложим. Получим значение суммарных затрат, для данного начального решения. F0=30*5+20*1+20*3+10*3+40*8+40*1+50*2=720 ден.ед. Проверим полученный план на оптимальность. Признак оптимальности опорного решения. Если допустимое решение Х=( 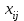 ), i=1,2,,…,m, j=1,2,…,n транспортной задачи является оптимальным, то существует потенциалы (числа) поставщиков ), i=1,2,,…,m, j=1,2,…,n транспортной задачи является оптимальным, то существует потенциалы (числа) поставщиков 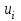 , i=1,2,,…,m и потребителей , i=1,2,,…,m и потребителей 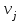 , j=1,2,…,n, удовлетворяющие следующим условиям: , j=1,2,…,n, удовлетворяющие следующим условиям: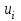 + +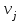 = =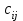 при при 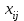 >0, >0, 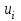 + +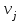 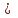 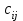 при при 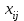 =0. =0. Для заполненных клеток составим систему: 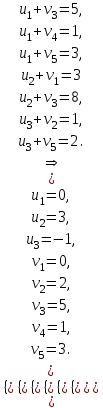 Расчеты представим в таблице:
Тогда для пустых клеток имеем: 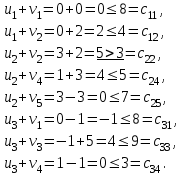 Критерий оптимальности не выполнен, так как есть клетка, для которой 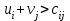 . . Для клетки (2,2) строим цикл пересчета. В клетку (2, 2) назначим min(40,20,40)=20.
F1=50*5+20*1+10*3+20*3+20*8+20*1+70*2=680 ден.ед. Аналогично проверим найденный план на оптимальность. Найдем потенциалы занятых клеток (представлены в таблице). Для свободных клеток найдем суммы потенциалов. 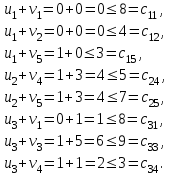 Критерий оптимальности выполнен. F*=680 ден.ед. Оптимальный план:
Ответ: Составлен оптимальный план перевозки грузов при котором общая стоимость перевозки всех грузов из пунктов отправления в пункты назначения является минимальной и равна 680 денежных единиц. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
