Апаркина. Задача 1 Рассчитайте эффект финансового рычага Исходные данные представлены в таблице
 Скачать 89.2 Kb. Скачать 89.2 Kb.
|
|
При увеличенииувеличится на 51%, а при уменьшении уменьшится на 51 %. Таблица – Результаты расчета при изменении цены капитала на 10 % как в сторону увеличения, так и в сторону уменьшения
При увеличении уменьшается на 2%, а при уменьшении увеличивается на 2%. Для предприятия первое значение имеет изменение цены. Задача №4 Рассматриваются два проекта А и Б относительно возможностей инвестирования. Известны прогнозные оценки значений дохода от каждого из этих проектов и соответствующие значения вероятностей. Статистическим методом оценить степень риска каждого из этих проектов и выбрать один из них для инвестирования. Мерой величины риска в статистическом методе признается колебание результатов. Мерой колебания результатов некоторого ряда под влиянием разных факторов вероятности служит целая группа статистических величин: дисперсия, среднеквадратичное отклонение, коэффициент вариации. Критерием выбора из нескольких инвестиционных проектов является минимум по коэффициент вариации. Таблица - Исходные данные
Найдем среднюю прибыль (  ) по проекту А и проекту Б. ) по проекту А и проекту Б.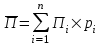 где  - средняя прибыль; - средняя прибыль;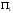 - прибыль; - прибыль;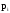 - вероятность получения прибыли. - вероятность получения прибыли.По проекту А  =400х0,3+500х0,4+2670х0,3+321х0,5+300х0,3=1371,50 =400х0,3+500х0,4+2670х0,3+321х0,5+300х0,3=1371,50По проекту Б  =2050х0,3+900х0,4+2179х0,3+700х0,5+2400х0,3=2698,70 =2050х0,3+900х0,4+2179х0,3+700х0,5+2400х0,3=2698,70Найдем дисперсию по проекту А и проекту Б. 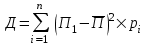 По проекту А Д (400-1371,5)2х0,3+(500-1371,5) 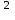 х0,4+(2670-1371,5) х0,4+(2670-1371,5)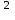 х0,3+(321-1371,5)2х0,5+(300-1371,5)2х0,3=4468232,17 х0,3+(321-1371,5)2х0,5+(300-1371,5)2х0,3=4468232,17По проекту Б Д (2050-2698,7)2х0,3+(900-2698,7)2х0,4+(2179-2698,7)2х0,3+(700-2698,7)2х0,5+(2400-2698,7)2х0,3=3525565,98 Найдем среднеквадратичное отклонение по проекту А и проекту Б σ = 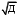 по проекту А  σ = 2113,82 σ = 2113,82по проекту Б  σ = 1877,65 σ = 1877,65Найдем коэффициент вариации по проекту А и проекту Б. Коэффициент вариации - это отношение среднего квадратического отклонения к средней арифметической. Он показывает степень отклонения полученных значений и рассчитывается по формуле 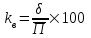 по проекту АКв= 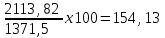 по проекту БКв= 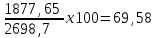 Коэффициент вариации – это относительная мера риска. Чем выше коэффициент вариации, тем выше уровень риска. Установлена следующая оценка коэффициентов вариации: до 10% - слабый уровень риска; 10-25% - умеренная уровень риска; свыше 25% - высокая уровень риска. Б принимаем. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
