Апаркина. Задача 1 Рассчитайте эффект финансового рычага Исходные данные представлены в таблице
 Скачать 89.2 Kb. Скачать 89.2 Kb.
|
|
Практическая часть Апаркина Задача №1 Рассчитайте эффект финансового рычага Исходные данные представлены в таблице Таблица – Расчет эффекта финансового рычага ОАО «ХХХ»
Определимизменениевеличины ЭФР за счет каждой с оставляющей данного показателя, последовательно заменяя базовый их уровень на фактический отчетного периода. ЭФРо = [(ВЕРо- Цнзко)х(1-Кн)х (ЗК /СК)] ЭФРо=[(31,30–3,28) х (1 – 0,2) х 3,05]= +68,38% ЭФРусловие1=[(24,55–3,28) х (1 – 0,2) х 3,05] = 51,89% ЭФРусловие2=[(24,55-3,56) х (1-0,2) х 3,05] = 51,22% ЭФРусловие3=[(24,55-3,56) х (1-0,22) х 3,05] = 49,94% ЭФРусловие4=[(24,55-3,56) х (1-0,22) х 4,33] = 70,89% Общиеизменение70,89 – 68,38 = 2,54 в том числе а) уровнярентабельностисовокупногокапитала 51,89-68,38=-16,49 б) средневзвешеннаяценазаемногокапитала 51,22-51,89=-0,67 в) уровняналоговогоизъятия 49,94-51,22=-1,28 г)плеча финансовогорычага 70,89-49,94 = +20,95 Сумма собственного капитала предприятия за сет заемного капитала увеличилась и составила 39289,68 тыс. руб. Следовательно в сложившийся ситуации выгодно использовать заемные средства в оборотепредприятия, так как в результатеэтогоповышается раз мер собственногокапитала. Задача №2 При выборе рациональной стратегии производства (оптовых закупок в сфере товарного обращения) в условиях неопределенности и риска можно использовать игровые модели. Применение игровых моделей предлагается на примере компании, которая имеет несколько каналов сбыта продукции определенного ассортимента. В розничной торговле с помощью этого примера можно определять объем оптовых закупок у поставщиков в зависимости от возможных колебаний платежеспособного спроса населения в районах реализации товара. В задаче есть три стратегии производства продукции (закупок в сфере обращения):S1, S2, S3. В зависимости от изменений рыночной конъюнктуры в связи с имеющимися возможностями реализации рассчитанные варианты среднегодовой прибыли, которые представлены в виде матрицы платежеспособного спроса, с учетом ожидаемого значения потерь в случае неудачного результата, связанных, например, с хранением нереализованной продукции, как следствие неиспользованных возможностей, нерационального распределения инвестиций, снижения оборотности оборотных средств, порчи или другими причинами. Значение матрицы определяются экспертным путем. Ниже приводятся платежные матрицы по вариантам, каждый элемент которых является среднегодовой прибылью (в млн. д.е. )в результате выбора одной из трех стратегий производства (закупок) при разных состояниях рыночной конъюнктуры. По условиям задачи требуется выбрать оптимальную стратегию производства (закупок). Для принятия решения в условиях неопределенности необходимо использовать: maxmaxкритерий; maxmin(критерий Вальда); minmax (критерий Сэвиджа); критерий пессимизма-оптимизма Гурвица (к=0,6); Для принятия решения в условиях риска необходимо использовать: критерий математического ожидания; критерий Лапласа Основываясь на полученных оценках выбрать оптимальную стратегию поведения предприятия на рынке. Таблица - Зависимость прибыли предприятия от состояния рыночной конъюнктуры и выбранной стратегии
Для принятия решения в условиях неопределенности необходимо использовать: maxmax критерий; Наилучшей признается стратегия, при которой достигается максимальная прибыль, равная: 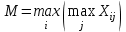 , ,Запись вида maxiозначает поиск максимума перебором столбцов, а запись вида maxj– поиск максимума перебором строк в матрице. Решение оформить в виде таблицы Таблица –Выбор стратегии по критерию maxmax
Следует заметить, что ситуации, требующие применения такого критерия, в общем, нередки, и пользуются им не только безоглядные оптимисты, но и игроки, вынужденные руководствоваться принципом «или пан — или пропал». Вывод: максимальное значение maxmax критерия получаем при S2 стратегии. maxmin (критерий Вальда); Еще называется «критерием пессимизма», т.к. при его использовании как бы предполагается, что от любого решения надо ожидать самых худших последствий и,следовательно, нужно найти такой вариант, при котором худший результат будет относительно лучше других худших результатов. Таким образом, он ориентируется на лучший из худших результатов. 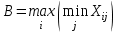 , ,Расчет состоит из 2 шагов. Находим худший результат каждой стратегии, т.е. величину minij и строим таблицу Таблица –Выбор стратегии по критерию maxmin (критерий Вальда)
Далее из худших результатов, представленных в столбце минимумов, выбираем лучший. Это перестраховочная позиция крайнего пессимиста. Такая стратегия приемлема, когда инвестор не столь заинтересован в крупной удаче, но хочет застраховать себя от неожиданных проигрышей. Выбор такой стратегии определяется отношением принимающего лица к риску. В соответствии с критерием maxmin (критерий Вальда) получаем стратегию S2 minmax (критерий Сэвиджа); Ориентирован не столько на минимизацию потерь, сколько на минимизацию сожалений по поводу упущенной прибыли. Он допускает разумный риск ради получения дополнительной прибыли. Пользоваться этим критерием для выбора стратегии поведения в ситуации неопределенности можно лишь тогда, когда есть уверенность в том, что случайный убыток не приведет фирму (проект) к полному краху: 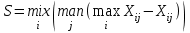 , ,Расчет данного критерия включает в себя 4 шага: Находим лучшие результаты каждого в отдельности столбца, т. е. тахХij. Это те максимумы, которые можно было бы получить, если бы удалось точно угадать возможные реакции рынка. Определяем отклонения от лучших результатов в пределах каждого отдельного столбца, т. е. maxХij - Хij. Получаем матрицу отклонений, которую можно назвать «матрицей сожалений», ибо ее элементы — это недополученная прибыль от неудачно принятых решений из-за ошибочной оценки возможной реакции рынка. Матрицу сожалений можно оформить в виде табл. Таблица – Матрицу сожалений
Для каждого варианта решения, т. е. для каждой строки матрицы сожалений, находим наибольшую величину. Получаем столбец максимумов сожалений в виде последнего столбца. Выбираем то решение, при котором максимальное сожаление будет меньше других. В соответствии с критериемminmax (критерий Сэвиджа) выбираем S1 стратегию. критерий пессимизма-оптимизма Гурвица; Критерий пессимизма-оптимизма Гурвнца при выборе решения рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом. То есть критерий выбирает альтернативу с максимальным средним результатом (при этом действует негласное предположение, что каждое из возможных состояний среды может наступить с равной вероятностью). Формально данный критерий выглядит так: 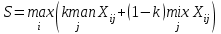 , ,где k — коэффициент пессимизма, который принадлежит промежутку от 0 до 1 в зависимости от того, как принимающий решение оценивает ситуацию. Если он подходит к ней оптимистически, то эта величина должна быть больше 0,5. При пессимистической оценке он должен взять упомянутую величину меньше 0,5. При k = 0 критерий Гурвица совпадает с критерием Вальда, а при k = 1 с критерием maxmax. Рассчитаем критерий Гурвица для условий нашего примера, придав упомянутому параметру значение на уровне 0,6. S1=0,6 х 63 +23 х (1-0,6)= 47 S2=0,6 х 92+(-4) х (1-0,6)=53,6 S3=0,6 х 28+(-8) х (1-0,6)=13,6 Стратегия S2,а если уровень равен 0,2,тогда: S1=0,2х 63+23 х (1-0,2)=31 S2=0,2х92 + (-4) х (1-0,2)=15,2 S3=0,2 х 28+(-8)х(1-0,2)=-0,8 Стратегия S1 при уровне 0,2. 5. критерий математического ожидания; Под ситуацией риск понимается такая ситуация, когда можно указать не только возможные последствия каждого варианта принимаемого решения, но и вероятности их появления. Критерий математического ожидания является основным критерием для принятия решения в ситуации риска. Ему соответствует формула: 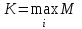 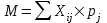 где 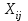 — выплата, которую можно получить в i-м состоянии «среды», — выплата, которую можно получить в i-м состоянии «среды», 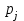 — вероятность j-гo состояния среды. — вероятность j-гo состояния среды.Таким образом, лучшей стратегией будет та, которая обеспечит инвестору (менеджеру) максимальный средний выигрыш. Воспользуемся данными нашего примера для иллюстрации критерия, добавив вероятности наступления возможных событий (табл.). Таблица – Критерий математического ожидания
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
