64вариант гидравлика. Задача 1 Решение
 Скачать 0.6 Mb. Скачать 0.6 Mb.
|
|
Задача № 1  Решение В общем случае для криволинейной стенки сила избыточного гидростатического давления определяется по двум составляющим, горизонтальной и вертикальной: Горизонтальная составляющая определяется по формуле: где ρ – плотность жидкости; g – ускорение свободного падения; hС – расстояние от центра тяжести площади вертикальной проекции стенки S до пьезометрической плоскости; S – площадь вертикальной проекции стенки. Вертикальная составляющая силы давления, воспринимаемой криволинейной стенкой, равна силе тяжести жидкости в объеме VВ, который ограничен стенкой, пьезометрической плоскостью и вертикальной проектирующей поверхностью, построенной на контуре стенки, и определяется по формуле: где ρ – плотность жидкости; g – ускорение свободного падения; VВ – сила тяжести жидкости в объеме. Рассмотрим крышку А (которая крепится группой болтов А). Прежде всего определим положение пьезометрической плоскости. Так как вакуумметр показывает «отрицательное» давление (меньше атмосферного), то пьезометрическая плоскость будет проходить ниже точки установки вакуумметра. Тогда Пьезометрическая плоскость проходит на 0,5 м ниже нижней образующей цилиндрической поверхности резервуара и сила давления воды для крышки А будет направлена внутрь сосуда. Определим горизонтальную составляющую (прижимающая нагрузка для группы болтов А). Определим вертикальную составляющую. Рассмотрим крышку В. Из аналогичных соображений определим горизонтальную составляющую. Определим вертикальную составляющую. Эта сила также направлена наружу сосуда (прижимающая нагрузка для группы болтов В). Рассмотрим крышку С. Сила давления на плоскую стенку в общем случае определяется по формуле: где ρ – плотность жидкости; g – ускорение свободного падения; hс – расстояние от центра тяжести площади вертикальной проекции стенки S до пьезометрической плоскости; S – смоченная площадь стенки. Эта сила направлена внутрь сосуда. Строим эпюру давления. 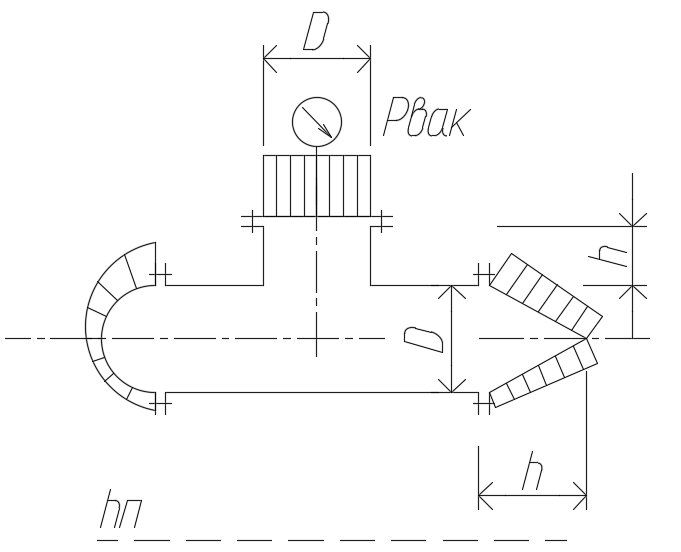 Задача № 2  Решение Запишем уравнение Бернулли для сечений 1-1 и 2-2. Сечение 1-1 совпадает со свободной поверхностью жидкости в левом резервуаре, а сечение 2-2 – в правом где z1, z2 – геометрический напор в соответствующих сечениях; р1, р2 – давление в соответствующих сечениях; υ1, υ2 – скорость потока жидкости в соответствующих сечениях; ρ – плотность жидкости; g – ускорение свободного падения; h1-2 – потери напора между сечениями 1-1 и 2-2. За плоскость сравнения примем плоскость, проходящую через сечение 2-2 Тогда: z1 = Н, z2 = 0; Примем, что резервуары достаточно велики, чтобы пренебречь изменением уровня в них. Тогда υ1=0; υ2=0; р1=р2=ратм=0 – т. е. избыточное давление равно нулю. Потери между сечениями 1-1 и 2-2 можно в общем виде определяются по формуле: h1-2 = где ζм – коэффициент местного сопротивления; λ – коэффициент потерь на трение по длине; l – длина участка трубопровода; d – диаметр участка трубопровода; V – скорость жидкости в трубопроводе; ρ – плотность жидкости. В данном случае удобно воспользоваться условием неразрывности потока где S - площадь поперечного сечения потока, в данном случае трубы. S = Тогда, пренебрегая местными потерями, можно записать В полученной формуле остается неизвестным коэффициент потерь на трение по длине λ, порядок нахождения которого зависит от режима течения. Режим течения определяется путем нахождения числа Рейнольдса. где ν – коэффициент кинематической вязкости воды. Так как диаметр неизвестен, то прямое определение числа Рейнольдса и, соответственно, коэффициента гидравлического трения не представляется возможным. Предположим, что режим течения турбулентный. Воспользуемся формулой Альтшуля, применимой для всей турбулентной области режимов течения: где Δ – эквивалентная абсолютная шероховатость. Тогда 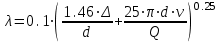 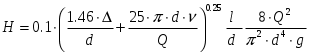 Подставляя численные значения, получим: Решая полученное уравнение методом последовательных приближений, получим d = 0,04 м. Также данное уравнение можно решить графоаналитческим способом, построив график зависимости H= f(d). Проверим предположение о режиме течения Так как Re>>2300, то режим течения турбулентный, и изначальное предположение верно. Задача № 3 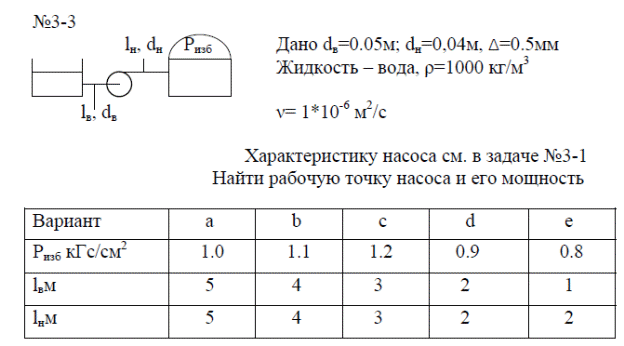 Решение В данной системе напор насоса расходуется на преодоление гидравлических сопротивлений в трубопроводах (всасывающем и напорном) и противодавления в приемном баке (разницей уровней в баках пренебрегаем). Следовательно, можно записать условие совместной работы насоса и сети: 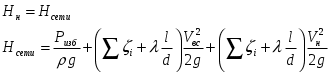 где ζм – коэффициент местного сопротивления.; λ – коэффициент потерь на трение по длине; l – длина участка трубопровода; d – диаметр участка трубопровода; V – скорость жидкости в трубопроводе; ρ – плотность жидкости. В данном случае удобно заменить в указанном выражении скорость расходом в трубопроводе, учитывая, что, по уравнению неразрывности где S – площадь поперечного сечения трубопровода. Тогда, пренебрегая местными сопротивлениями, можно записать: Зададимся Q=3 л/с=3∙10-3 м3/с Скорость во всасывающей линии 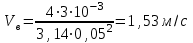 Число Рейнольдса определяется по формуле: где 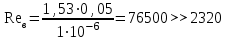 Определим 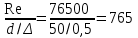 >500, это квадратичная область сопротивления, потому коэффициент гидравлического трения можно определять по формуле: >500, это квадратичная область сопротивления, потому коэффициент гидравлического трения можно определять по формуле: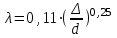 , где Δ– эквивалентная шероховатость стенок трубы , где Δ– эквивалентная шероховатость стенок трубы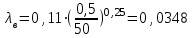 В напорной линии скорость будет еще выше, потому область сопротивления также квадратичная. 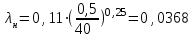 Воспользуемся характеристикой насоса задачи №3-1:  Все расчеты занесем в общую таблицу
На пересечении линий потребного напора и характеристики насоса находим рабочую точку насоса. 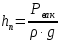 На пересечении характеристик насоса и сети получаем рабочую точку с параметрами Н≈ 13,8 м, Q ≈ 5 л/с, η ≈ 70 %. Определим мощность на валу насоса |
