контрольная микроэкономика. Вариант 5. Задача 1 в лотерее 1000 билетов, из них половина выигрышные. Куплено два. Какова вероятность того, что оба билета выигрышные
 Скачать 100.5 Kb.
|
|
Вариант 5 задача №1 В лотерее 1000 билетов, из них половина выигрышные. Куплено два. Какова вероятность того, что оба билета выигрышные? Решение А- событие, состоящее в том, что оба билета выигрышные 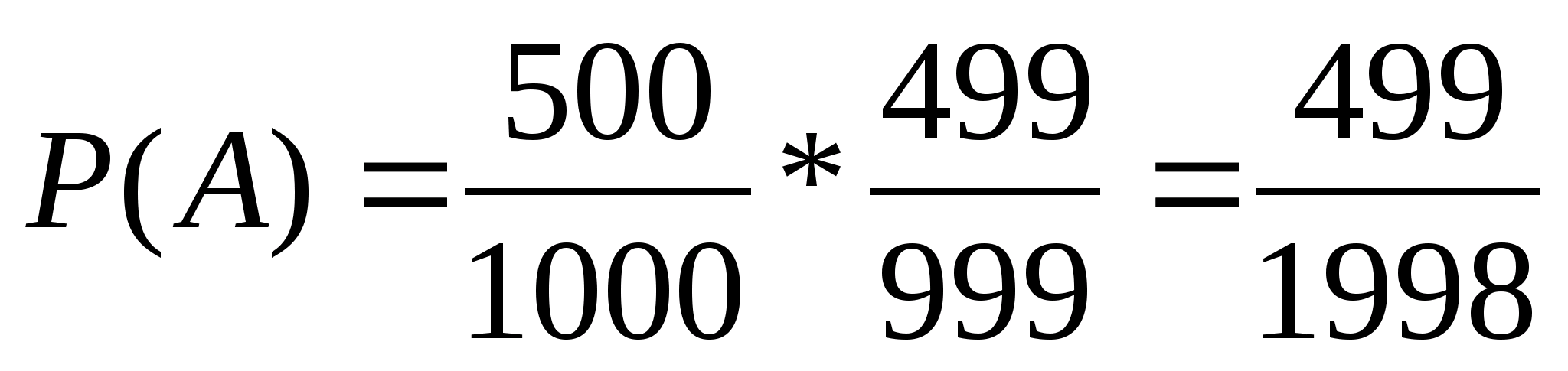 Электрический провод, соединяющий пункты А и В порвался в неизвестном месте. Чему равна вероятность того, что разрыв произошел не далее 500 метров от пункта А если расстояние между пунктами равно 2 км? В студии телевидения 3 телекамеры. Для каждой камеры вероятность того, что она включена в данный момент равна 0,7. Найти вероятность того, что в данный момент включена хотя бы одна камера. Возле остановки «Космос» останавливаются автобусы маршрутов №№ 16, 15, 11, 21, 9. Для рабочего попутным являются маршруты №№ 15, 21. Найти вероятность того, что к остановке первым подойдет автобус маршрута попутного для рабочего, если известно, что на линиях по маршрутам №№ 16, 15, 11, 21, 9 курсируют в этот день соответственно 15, 10, 8, 5, 12 автобусов. Вероятность того, что стрелок при стрельбе по мишени выбьет 10 очков равна 0,15; 9 очков - 0,2; 8 очков - 0,3; 7 очков - 0,35. Найти вероятность того, что стрелок выбьет более 7 очков. На десяти одинаковых карточках написаны буквы, составляющие слово «математика». Карточки тщательно перемешивают и вынимают 4, раскладывая их в ряд одну за другой. Какова вероятность, что появится слово «мама»? У сборщика имеется 3 коробки деталей, изготовленных заводом № 1, 4 - изготовленных заводом № 2. Вероятность того, что деталь завода № 1 стандартна равна 0,7, а для завода № 2 - 0,9. Наудачу извлечена деталь. Найти вероятность того, что вынутая деталь стандартна. Имеется три одинаковых по виду ящика. В первом ящике 20 белых шаров, во втором - 10 белых и 10 черных шаров, в третьем - 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Найти вероятность того, что шар вынут из первого ящика. Монету бросают 6 раз. Что вероятнее: герб выпадет не менее трех раз или не более трех раз? Предполагая, что вероятность поражения мишени при одном выстреле равна 0,6. Найти вероятности следующих событий: 1) при 12 выстрелах мишень будет поражена 7 раз; 2) при 200 выстрелах цель будет поражена не менее 110, но не более 130. Вариант 5 Производится 2 независимых выстрела с вероятностями попадания в цель соответственно 0,6 и 0,5. X - число попаданий в мишень. Для этой случайной величины: а) построить ряд распределения, многоугольник распределения, функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность поражения цели. Непрерывная случайная величина задана интегральной функцией: 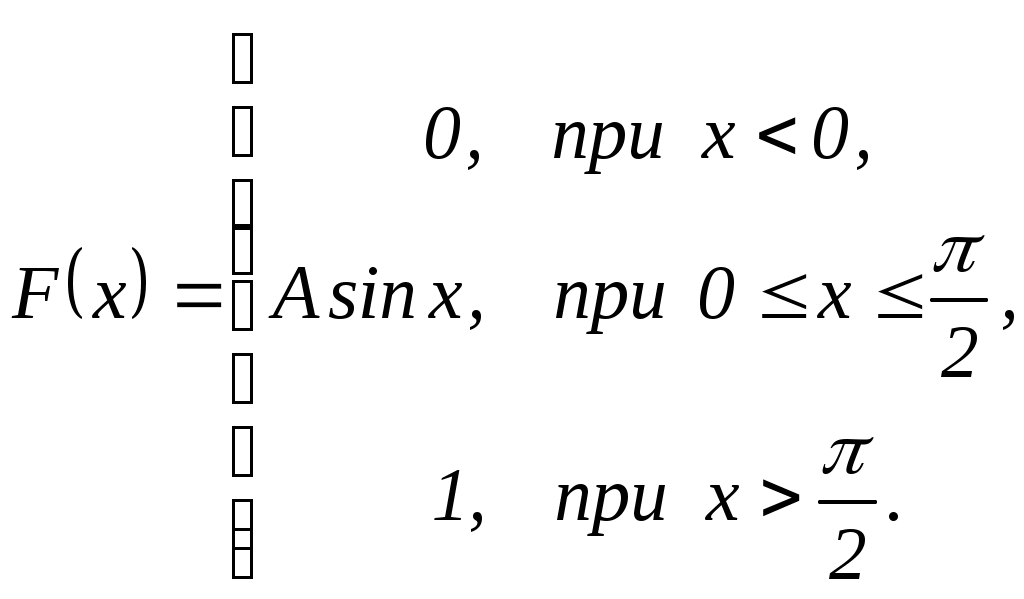 Найти а) коэффициент А; б) дифференциальную функцию  ; в) математическое ожидание, дисперсию, среднее квадратичное отклонение; г)  . Построить графики и  .Непрерывная случайная величина задана дифференциальной функцией: 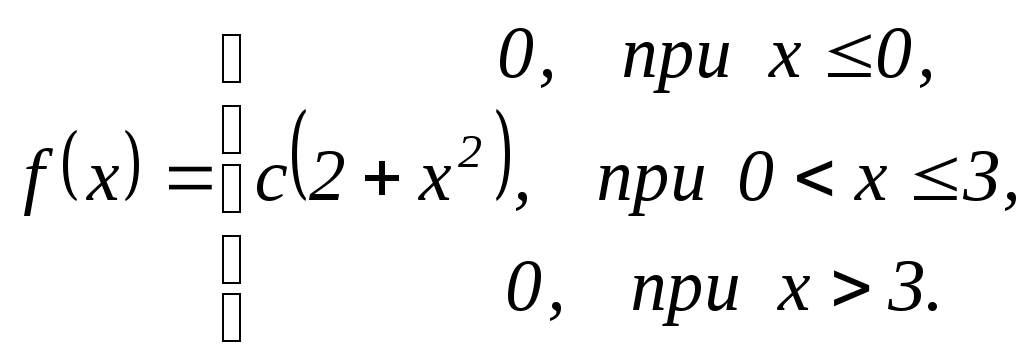 Найти а)параметр с; б) интегральную функцию распределения  ; в) математическое ожидание, дисперсию, среднее квадратичное отклонение; г)  . Построить графики и . Изобразить вероятность .Вычислить двумя способами  и  , если заданы законы распределения случайных величин:
Найти вероятность попадания в интервал  нормально распределенной случайной величины X, если известны ее математическое ожидание  и среднее квадратичное отклонение  .Найти закон распределения дискретной случайной величины Х, которая имеет только два возможных значения  и  , причём  . Математическое ожидание  , дисперсия  , возможное значение случайная величина Х принимает с вероятностью  .Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час, равно 3. Найти вероятность того, что за 2 часа поступит менее двух заявок, если число заявок распределено по закону Пуассона. |