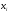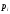Высшая математика. Теория вероятностей_17 вар.. Задача 17. В некотором цехе брак составляет 4% всех изделий. Случайная величина
 Скачать 133.65 Kb. Скачать 133.65 Kb.
|
|
Задача 9.17. В некотором цехе брак составляет 4% всех изделий. Случайная величина ξ – число бракованных изделий среди наугад взятых 3 изделий. Решение: Случайная величина ξ – бракованных изделий среди наугад взятых. Значения, которые может принимать данная случайная величина ξ: 0, 1, 2, 3. Отбор бракованных изделий независимы один от другого, вероятности отбора бракованных изделий равны между собой, поэтому применима формула Бернулли. Учитывая, что, по условию, 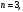 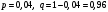 , получим: , получим: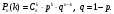 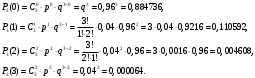 Проверяем полную вероятность: 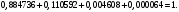 Тогда закон распределения случайной величины X:
Ответ:
Задача 10.17. На станцию метро в течение определенного времени суток направляется простейший поток пассажиров с плотностью 180 чел./ч. Найти вероятность того, что: а) за 2 мин на станцию войдут ровно 7 пассажиров; б) за 0,1 мин на станцию войдут хотя бы 2 пассажира; в) за 1 мин на станцию не войдет ни один пассажир. Решение: По условию 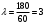 . События, состоящие в том, что на станцию зайдут пассажиры, независимы. Воспользуемся формулой Пуассона: . События, состоящие в том, что на станцию зайдут пассажиры, независимы. Воспользуемся формулой Пуассона: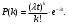 а) Найдем вероятность того, что за 2 мин на станцию войдут ровно 7 пассажиров 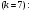 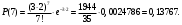 б) Найдем вероятность того, что за 0,1 мин на станцию войдут хотя бы 2 пассажира: 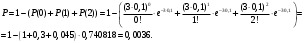 в) Найдем вероятность того, что за 1 мин на станцию не войдет ни один пассажир: 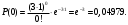 Ответ: а) 0,13767; б) 0,0036; в) 0,04979. Задача 11.17. Для непрерывной случайной величины ξ дана функция распределения 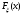 , содержащая параметр a. Найти: , содержащая параметр a. Найти:а) значение параметра a; б) плотность распределения 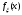 и построить графики функций и построить графики функций 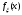 и и 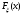 ; ;в) вероятность попадания НСВ ξ на отрезок [b; c]; г) основные числовые характеристики: 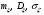 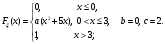 Решение: а) Постоянную aнайдем из условий: 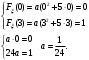 Функция распределения имеет вид: 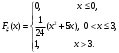 б) Найдем плотность распределения 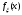 : :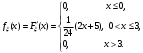 Построим 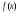 и и 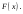 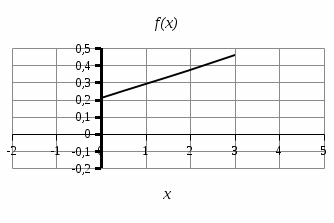  в) Вероятность того, что случайная величина X примет значение, принадлежащее отрезок [b; c] вычислим по формуле: 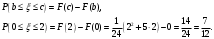 г) Математическое ожидание равно: 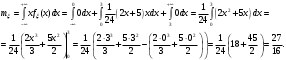 Дисперсия: 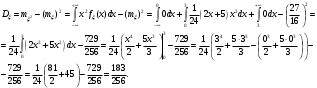 Среднеквадратическое отклонение: 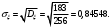 Задача 12.17. Автобусы некоторого маршрута идут строго по расписанию с интервалом движения 5 мин. Пусть случайная величина ξ – время ожидания автобуса пассажиром, подошедшим к остановке в некоторый момент времени, распределена равномерно. Требуется найти: а) плотность вероятности 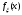 и функцию распределения и функцию распределения 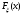 ; ;б) вероятность того, что пассажир будет ожидать очередной автобус менее 2 мин; в) среднее время ожидания автобуса и дисперсию времени ожидания. Решение: а) Плотность распределения случайной величины ξ, распределенной равномерно в интервале вычисляется по формуле: 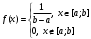 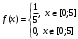 Функция распределения случайной величины ξ, распределенной равномерно в интервале вычисляется по формуле: 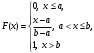 Подставим значения в формулу, получим: 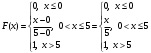 б) вероятность попадания случайной величины в интервал (4; 5) вычислим по формуле: 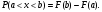 Вероятность того, что пассажир будет ожидать очередной автобус менее 2 мин, равна: 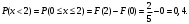 в) Математическое ожидание вычислим по формуле: 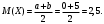 Дисперсию вычислим по формуле: 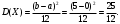 Задача 13.17. Испытываются два независимо работающий элементов. Длительность времени безотказной работы каждого элемента имеет показательное распределение с параметрами соответственно 0,01 и 0,02. Записать плотность вероятности 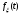 для каждого элемента и найти вероятность того, что в течение времени t = 50 (в часах): для каждого элемента и найти вероятность того, что в течение времени t = 50 (в часах):а) оба элемента будут работать; б) откажет хотя бы один элемент. Решение: Плотность вероятности случайной величины ξ, имеющей показательное распределение с параметром 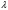 вычисляется по формуле: вычисляется по формуле: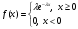 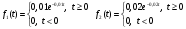 а) Найдем вероятность того, что в течение времени t = 50 (в часах) оба элемента будут работать: 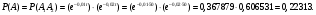 б) Событие B – хотя бы один элемент откажет. 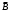 – ни один элемент не откажет. – ни один элемент не откажет.Искомая вероятность вычислим по формуле: 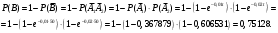 Задача 14.17. Расстояние, на котором обнаруживается радиолокационной станцией маловысотная цель, является случайной величиной ξ, подчиненной нормальному закону с параметрами m = 80 км и σ = 20 км. Требуется: а) записать выражение для плотности вероятности 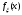 ; ;б) найти вероятность обнаружения цели на расстоянии, большем чем 65 км; в) найти вероятность того, что обнаружение цели произойдет на расстоянии от 65 до 90 км; г) определить максимальное расстояние, на котором цель обнаруживается с вероятностью не менее 0,785. Решение: а) Формула плотности нормального закона распределения имеет вид: 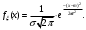 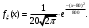 б) Вероятность попадания случайной величины в интервал (α; β) вычислим по формуле: 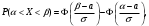 где 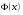 – функция Лапласа, которая находится по таблице значения функции Лапласа. – функция Лапласа, которая находится по таблице значения функции Лапласа. Искомая вероятность равна: 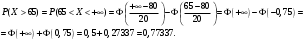 в) вероятность того, что обнаружение цели произойдет на расстоянии от 65 до 90 км равна: 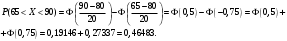 г) Найдем искомый интервал с помощью формулы: 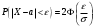 Учитывая, что неравенство 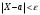 равносильно неравенству равносильно неравенству 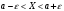 , получим , получим 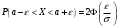 . .По условию эта вероятность равна 0,785, следовательно: 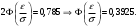 По таблице значений функции Лапласа находим 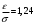 . Отсюда, . Отсюда, 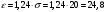 . Таким образом, искомый интервал имеет вид: . Таким образом, искомый интервал имеет вид: 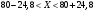 или или 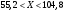 . . Значит максимальное расстояние, на котором цель обнаруживается с вероятностью не менее 0,785 равна 104,8 км. |