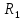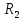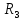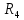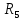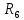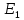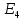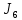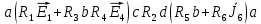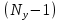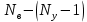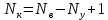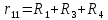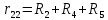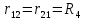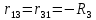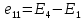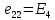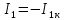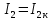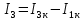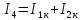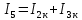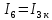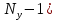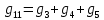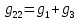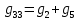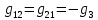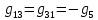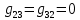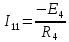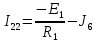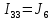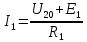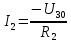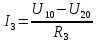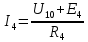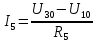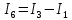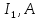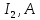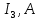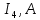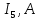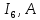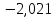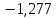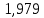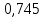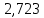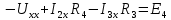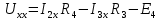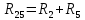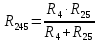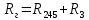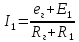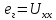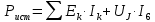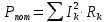КР №2.1. Задача 2. 1 Для электрической схемы, соответствующей номеру варианта и изображенной на рис. 1, выполнить следующее
 Скачать 306.94 Kb. Скачать 306.94 Kb.
|
Задача №2.1Для электрической схемы, соответствующей номеру варианта и изображенной на рис. 1, выполнить следующее: Начертить схему электрической цепи с обозначением узлов и элементов ветвей, соблюдая требования ЕСКД. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы. Определить токи во всех ветвях схемы методом контурных токов. Определить токи во всех ветвях схемы методом узловых потенциалов. Результаты расчета токов, проведенного двумя методами, свести таблицу и сравнить их между собой. Составить баланс мощностей в исходной схеме (схеме с источником тока), вычислив отдельно суммарную мощность источников и суммарную мощность нагрузок (сопротивлений). Определить ток I1 в заданной по условию схеме с источником тока, используя методом эквивалентного генератора. Таблица 1 – Исходные данные
Таблица 2 – Вариант схем для задачи
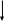                   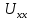 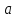 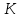 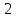 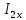 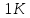 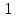 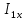  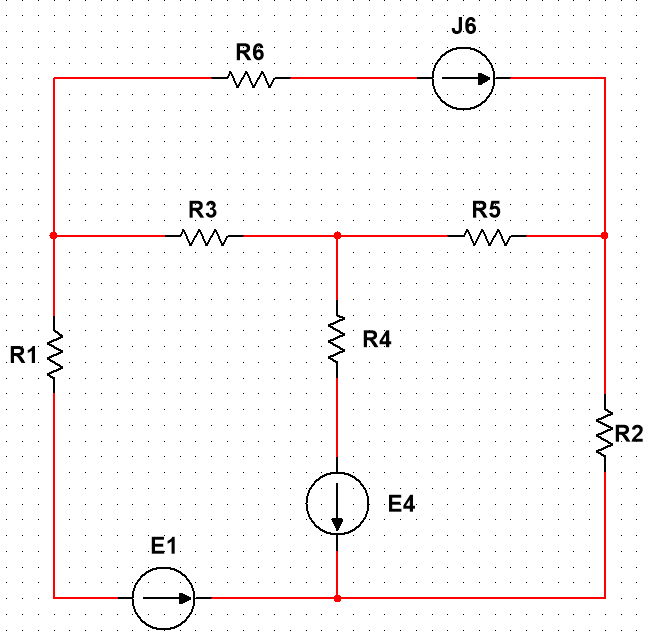 Рисунок 1 – Схема №1 Метод уравнений Кирхгофа Решение: а) Составим систему уравнения для схемы №1. Выберем условно положительное направление (УПН) в схеме №2. УПН выбираем произвольно. 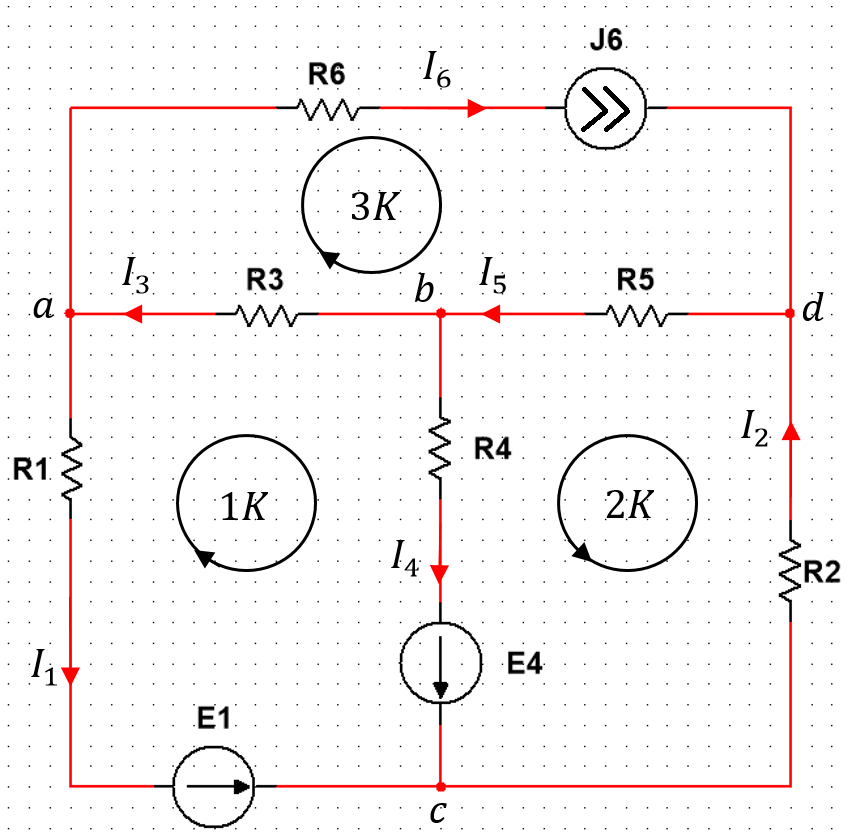 Рисунок 2 – Схема №1 с обозначенными токами, узлами и контурами Количество уравнений на основе первого закона Кирхгофа вычисляется по следующей формуле:
где: 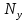 — число узлов. — число узлов.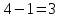 По второму закону Кирхгофа количество уравнений вычисляются по данной формуле:
где: 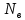 — число ветвей (ветвь с источником тока не учитывается). — число ветвей (ветвь с источником тока не учитывается).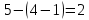 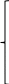 Составим систему уравнения по первому и второму закону Кирхгофа: Составим систему уравнения по первому и второму закону Кирхгофа: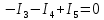 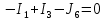 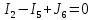 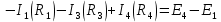 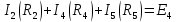 Решая полученную систему уравнений, известными из математики методами, можно было бы определить токи в ветвях. По условию решать систему уравнений не требуется. Расчет цепи методом контурных токов Количество уравнений для этого метода равно количеству уравнений, требуемых по второму закону Кирхгофа. Найдём токи в ветвях схемы методом контурных токов, для этого зададим произвольно направление токов в ветвях. Выберем произвольно направление обходов контуров. Количество необходимых уравнений вычисляется по формуле:
где: 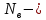 число ветвей (ветвь с источником тока не учитывается); число ветвей (ветвь с источником тока не учитывается);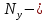 количество узлов. количество узлов.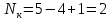 Для применения этого метода выделяем два независимых контура. (Независимыми контурами называются те контуры, у которых существует хотя бы одна ветвь, не входящая в остальные рассматриваемые контуры). 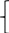 Составим систему уравнений для первого, второго и третьего контуров. Составим систему уравнений для первого, второго и третьего контуров. 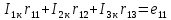 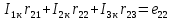 Определим собственные сопротивления контуров:
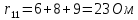 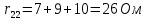 Теперь посчитаем общие сопротивления ветвей:
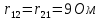 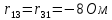 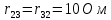 Рассчитаем необходимые значения э.д.с для решения системы уравнений:
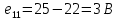 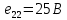 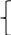 Подставим все значения сопротивлений и э.д.с: Подставим все значения сопротивлений и э.д.с: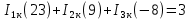 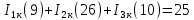 Решая полученную систему уравнений, известными из математики методами, мы получаем следующие ответы: 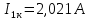 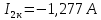 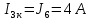 Рассчитываем действительные значения токов в ветвях:
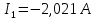 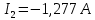 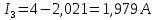 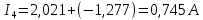 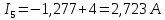 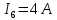 Расчет методом узловых потенциалов Количество уравнений необходимых для решения данной задачи определяется по следующей формуле:
где 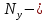 число узлов. число узлов.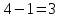 Для решения этим методом произвольно направляем токи в ветвях. Заземляем любой узел, например узел “с”, и составляем для оставшихся трех узлов уравнения по первому закону Кирхгофа. 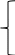 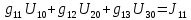 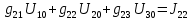  Далее необходимо рассчитать проводимости узлов. Собственная проводимость узла складывается из проводимостей ветвей, сходящихся в узле, и берётся со знаком плюс, проводимость же ветви, соединяющей узлы, берётся со знаком минус. Для начала рассчитаем собственные проводимости узлов:
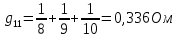 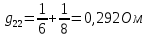 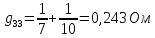 Теперь найдем проводимости ветвей, соединяющих узлы:
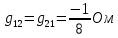 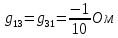 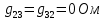 Следующим шагом находим значения задающих токов:
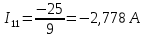 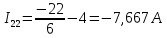 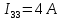 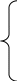 Подставляем найденные данные в систему уравнений: Подставляем найденные данные в систему уравнений: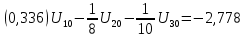 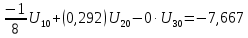 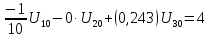 Решив систему уравнений, мы получим: 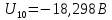 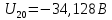 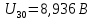 Зная напряжения узлов, можно без труда вычислить токи в ветвях. Рассчитаем токи в ветвях:
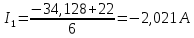 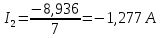 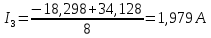 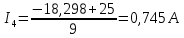 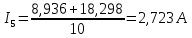 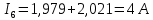 Сравнение результатов расчета Результаты расчетов обеими методами сводим в таблицу №3. Таблица 3 – Результаты расчетов
Расчет тока в ветви методом эквивалентного генератора Применяя метод эквивалентного генератора, определяем ток в одной ветви. Выберем 1ю ветвь. 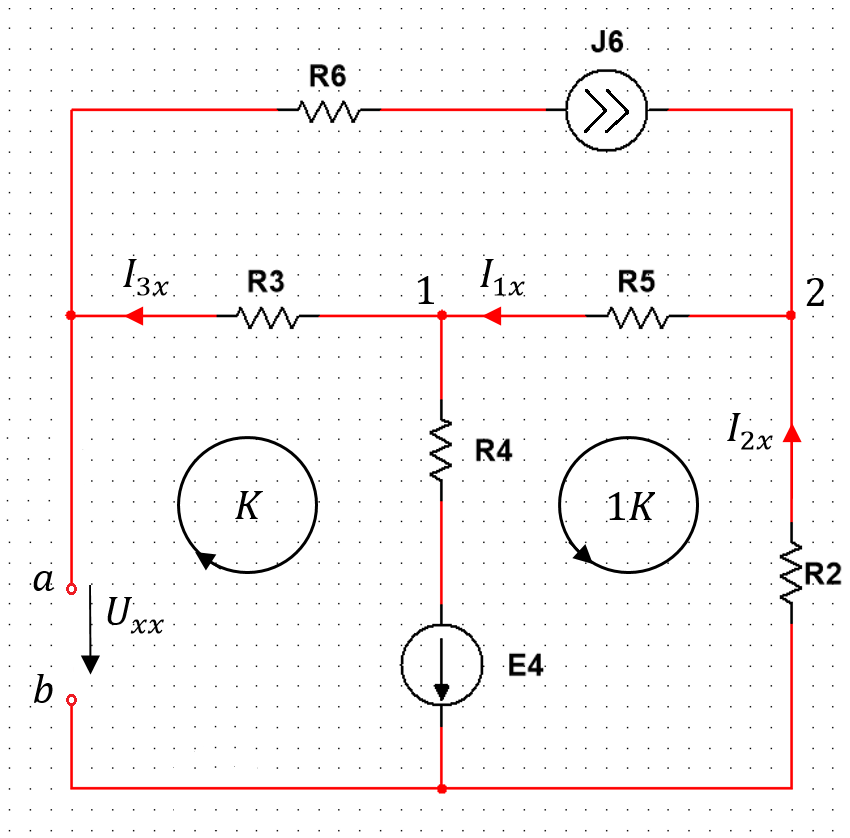 Рисунок 3 — Разомкнутая схема Разорвем ветвь и рассчитаем режим холостого хода, то есть определим напряжение на свободных зажимах. Это напряжение и будет являться значением эквивалентной ЭДС. Определим 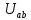 по выражению: по выражению:
Определим 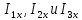 c помощью законов Кирхгофа. c помощью законов Кирхгофа.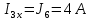 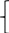 Составим систему уравнений: Составим систему уравнений: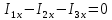 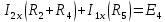 Решив систему уравнений, мы получаем следующие ответы: 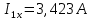 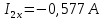 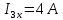 Определим 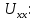 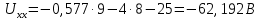 Сопротивление эквивалентного генератора равно сопротивлению между зажимами а и b, при условии, что все источники напряжения равны нулю (заменены внутренними сопротивлениями), а источники тока образуют разрыв цепи, как показано на рис. 4. 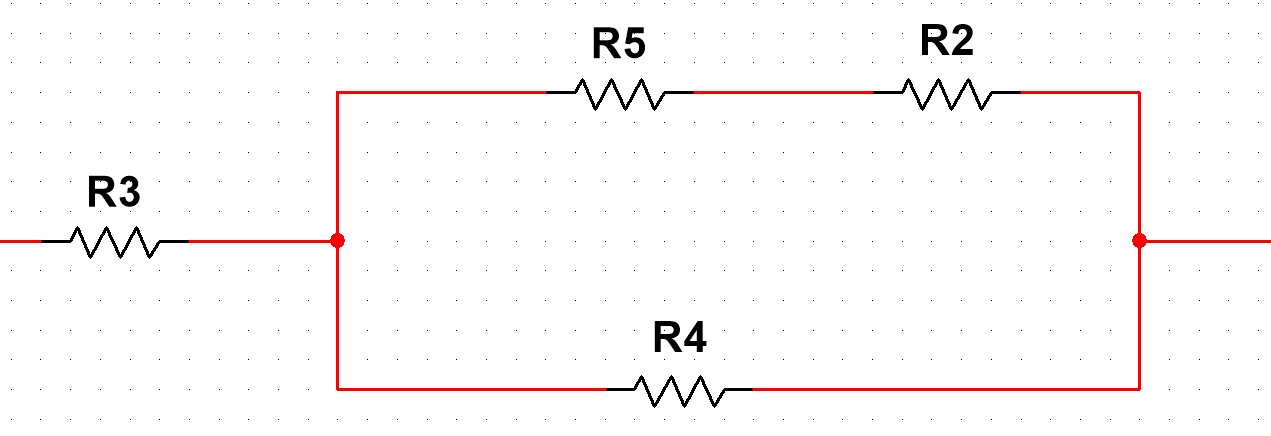 Рисунок 4 – Схема сопротивлений эквивалентного генератора Определим полное сопротивление генератора:
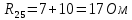 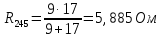 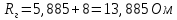 Для нахождения нужного нам тока упростим схему на рис. 5 и приведём её к следующему виду: 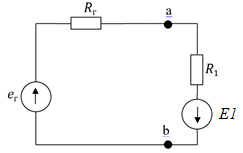 Рисунок 5 – Упрощенная схема Исходя из схемы, можно воспользоваться следующей формулой для расчёта нужного нам тока:
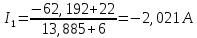 Значение этого тока совпадает с расчетами другими методами. Баланс мощностей Проверяем правильность решения задачи составлением баланса мощностей. Мощность, отдаваемая источниками энергии в цепь:
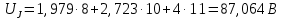 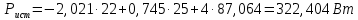 Мощность, потребляемая цепью, с учетом внутренних сопротивлений источников ЭДС:
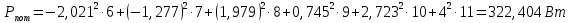 Баланс мощностей сходится, следовательно, токи определены, верно. Незначительным расхождением допускается пренебречь. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||