Главная страница
Навигация по странице:

  • Выигрыша (сокращение пробега) нет.

    		•

    Математические модели в транспортных системах. Математические модели в транспортных системах КР-2. Задача 2 Решить графическим методом задачу линейного программирования, при ограничениях 1,24х 1 0,8х 2 2,4


    Скачать 328.59 Kb.
    НазваниеЗадача 2 Решить графическим методом задачу линейного программирования, при ограничениях 1,24х 1 0,8х 2 2,4
    АнкорМатематические модели в транспортных системах
    Дата25.11.2020
    Размер328.59 Kb.
    Формат файлаdocx
    Имя файлаМатематические модели в транспортных системах КР-2.docx
    ТипЗадача
    #153569
    страница4 из 4
    1   2   3   4

    Подробноонахождениипотенциалов

      Поставщик  
    Потребитель
     QAi 

    B 1
    B 2
    B 3
    B 4
    B 5

    A 1
    10

    5
    8
    14
    7
    5

    0
      u1 = 0  

    A 2
    10
    5

    7
    11
    6
    10

    0
      u2 = 0  

    A 3
    10
    11
    9
    10

    5
    10

    0
      u3 = 0  

    A 4
    9
    12
    15

    8
    7
    10

    0
      u4 = 0  

    QBj
    v1 = 5
    v2 = 7
    v3 = 8
    v4 = 5
    v5 = 0






    Найдем оценки незадействованных маршрутов (cij - стоимость доставки).

    A1B2 :  
    Δ12 = c12 - ( u1 + v2 ) = 8 - ( 0 + 7 ) = 1

    A1B3 :  
    Δ13 = c13 - ( u1 + v3 ) = 14 - ( 0 + 8 ) = 6

    A1B4 :  
    Δ14 = c14 - ( u1 + v4 ) = 7 - ( 0 + 5 ) = 2

    A2B1 :  
    Δ21 = c21 - ( u2 + v1 ) = 10 - ( 0 + 5 ) = 5

    A2B3 :  
    Δ23 = c23 - ( u2 + v3 ) = 11 - ( 0 + 8 ) = 3

    A2B4 :  
    Δ24 = c24 - ( u2 + v4 ) = 6 - ( 0 + 5 ) = 1

    A3B1 :  
    Δ31 = c31 - ( u3 + v1 ) = 10 - ( 0 + 5 ) = 5

    A3B2 :  
    Δ32 = c32 - ( u3 + v2 ) = 11 - ( 0 + 7 ) = 4

    A3B3 :  
    Δ33 = c33 - ( u3 + v3 ) = 9 - ( 0 + 8 ) = 1

    A4B1 :  
    Δ41 = c41 - ( u4 + v1 ) = 9 - ( 0 + 5 ) = 4

    A4B2 :  
    Δ42 = c42 - ( u4 + v2 ) = 12 - ( 0 + 7 ) = 5

    A4B4 :  
    Δ44 = c44 - ( u4 + v4 ) = 7 - ( 0 + 5 ) = 2





    Нет отрицательных оценок. Следовательно, уменьшить общую стоимость доставки продукции невозможно.

    Ответ:

    X опт =


    10
    0
    0
    0
    5





    0
    5
    0
    0
    10

    0
    0
    0
    10
    10

    0
    0
    15
    0
    10


    Smin = 255 ден. ед.

    Задача 5

    Решить однопродуктовую задачу динамического программирования следующего вида:

    Вариант

    Затраты при распределении ресурса Х по вариантам

    Х = 0
    Х = 20
    Х = 40
    Х = 60



    1
    0
    20
    38
    69



    2
    0
    22
    41
    70



    3
    0
    19
    42
    71



    4
    0
    18
    43
    68




    Необходимо распределить ресурс общим объемом Q0 = 60 по вариантам (схемам) таким образом, чтобы получить минимальные суммарные затраты.

    Решение

    Задача 6

    Найти выигрыш (сокращение пробега) от объединения двух маршрутов 6 – 1 – 6 и 6 – 3 – 6 в один сборочно-развозочный, который выполняется на транспортной сети, приведенной в задаче 3.
    Решение

    Получаем следующую сеть: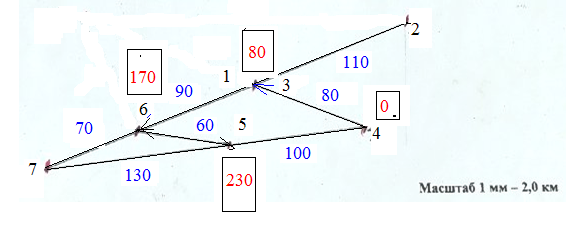


    Очевидно, что в нашем случае все останется без изменений, так как

    6 – 1 – 6 и 6 – 3 – 6 по 90 км.

    В итоге наименьший пробег:



    80 + 90 + 60 +100 = 330 км
    Выигрыша (сокращение пробега) нет.


    1   2   3   4

    написать администратору сайта