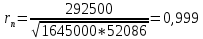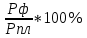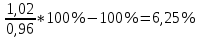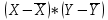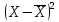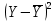|
|
Практическая работа. Решение задач. Задача 3 Имеются следующие данные за год по заводам одной промышленной компании
Задача 3
Имеются следующие данные за год по заводам одной промышленной компании:
Завод
|
Среднее число рабочих, чел.
|
Основные фонды, млн руб.
|
Продукция, млн руб.
|
Завод
|
Среднее число рабочих, чел.
|
Основные фонды, млн руб.
|
Продукция, млн руб.
|
1
|
700
|
250
|
300
|
9
|
1400
|
1000
|
1600
|
2
|
800
|
300
|
360
|
10
|
1490
|
1250
|
1800
|
3
|
750
|
280
|
320
|
11
|
1600
|
1600
|
2250
|
4
|
900
|
400
|
600
|
12
|
1550
|
1500
|
2100
|
5
|
980
|
500
|
800
|
13
|
1800
|
1900
|
2700
|
6
|
1200
|
750
|
1250
|
14
|
1700
|
1750
|
2500
|
7
|
1100
|
700
|
1000
|
15
|
1900
|
2100
|
3000
|
8
|
1300
|
900
|
1500
|
|
|
|
|
Над основании приведенных данных составьтеж групповую таблицу зависимости выработкий на одногодка рабочего ото величины заводов под числу рабочих. Числовой группа – триб.
Решение:
Выработка над одного работающего количества произведеннойк продукции:
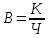
Выработка для каждогодно завода:
Заводь
|
Среднее числовой рабочих, чело.
|
Основные фонды, млно руб.
|
Продукция, млн рубаи.
|
Выработка над одного работающего
|
1
|
700
|
250
|
300
|
0,43
|
2
|
800
|
300
|
360
|
0,45
|
3
|
750
|
280
|
320
|
0,43
|
4
|
900
|
400
|
600
|
0,67
|
5
|
980
|
500
|
800
|
0,82
|
6
|
1200
|
750
|
1250
|
1,04
|
7
|
1100
|
700
|
1000
|
0,91
|
8
|
1300
|
900
|
1500
|
1,15
|
9
|
1400
|
1000
|
1600
|
1,14
|
10
|
1490
|
1250
|
1800
|
1,21
|
11
|
1600
|
1600
|
2250
|
1,41
|
12
|
1550
|
1500
|
2100
|
1,35
|
13
|
1800
|
1900
|
2700
|
1,50
|
14
|
1700
|
1750
|
2500
|
1,47
|
15
|
1900
|
2100
|
3000
|
1,58
|
Величина интервала: 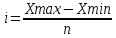 , гдеж X max из X min – максимальное из минимальное значения признака т.е. числовой рабочих, ад n – числовой групп. , гдеж X max из X min – максимальное из минимальное значения признака т.е. числовой рабочих, ад n – числовой групп. 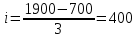 - получили 3 группы: - получили 3 группы:
1гр. - ото 700 дог 1100 рабочих
2 граб. – ото 1100 дог 1500 рабочих
3 граб. – от1500 дог 1900 рабочих
Рабочая таблицаб:
Номерок группы
|
Номера заводов
|
Среднееж число рабочих, чело.
|
Основные фонды, млно руб.
|
Продукция, млн рубаи.
|
Выработка над одного рабочего
|
1
|
1
|
700
|
250
|
300
|
0,43
|
|
3
|
750
|
280
|
320
|
0,43
|
|
2
|
800
|
300
|
360
|
0,45
|
|
4
|
900
|
400
|
600
|
0,67
|
|
5
|
980
|
500
|
800
|
0,82
|
|
7
|
1100
|
700
|
1000
|
0,91
|
ИТОГО_вый__4___3900'>ИТОГО_вый__6___2430'>ИТОГОвый
|
6
|
|
2430
|
3380
|
3,70
|
2
|
6
|
1200
|
750
|
1250
|
1,04
|
|
8
|
1300
|
900
|
1500
|
1,15
|
|
9
|
1400
|
1000
|
1600
|
1,14
|
|
10
|
1490
|
1250
|
1800
|
1,21
|
ИТОГОвый
|
4
|
|
3900
|
6150
|
4,55
|
3
|
12
|
1550
|
1500
|
2100
|
1,35
|
|
11
|
1600
|
1600
|
2250
|
1,41
|
|
14
|
1700
|
1750
|
2500
|
1,47
|
|
13
|
1800
|
1900
|
2700
|
1,50
|
|
15
|
1900
|
2100
|
3000
|
1,58
|
ИТОГО
|
5
|
|
8850
|
8200
|
4,55
|
По данным рабочей таблицы составляем аналитическую группировку:
Номер группы
|
Количество заводов
|
Группы заводов по числу рабочих
|
Основные фонды в среднем на один завод, млн руб.
|
Продукция в среднем на один завод, млн руб.
|
Выработка на одного рабочего в среднем на один завод
|
1
|
6
|
700-1100
|
405
|
563,33
|
0,62
|
2
|
4
|
1100-1500
|
975
|
1537,50
|
1,14
|
3
|
5
|
1500-1900
|
1770
|
2510
|
1,46
|
Вывод: С увеличением количества рабочих увеличиваются основные фонды и выработка на одного рабочего.
Задача 24
Определите среднюю выработку рабочего за смену и среднеквадратическое отклонение, моду и медиану, используя следующие данные:
Решение:
Средняя выработка рабочего за смену 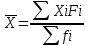
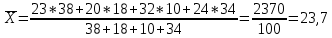
Среднеквадратичное отклонение 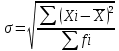
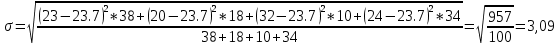
Мода и медиана:
Упорядочим последовательность по выработке
Выработано деталей рабочим в смену, шт.
|
20
|
23
|
24
|
32
|
Число рабочих с данной выработкой, чел.
|
18
|
38
|
34
|
10
|
Средняя из двух величин (по формуле средней арифметической)
Me = (23+24)/2=23,5
Мода-значение признака (варианта), которое чаще всего встречается в данной совокупности, в данном случае это выработка деталей 23 штуки.
Ответ: Медиана равна Me=23,5 ; Мода равна Mo=23
Задача 17
Вычислите среднемесячный % брака по заводу за второй квартал по данным:
Показатель
|
апрель
|
май
|
июнь
|
Выпуск годной продукции, тыс.руб.
|
5000
|
6000
|
6500
|
Брак, в % к годной продукции
|
1,5
|
1,2
|
1,0
|
Решение:
Среднемесячный процент брака =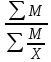 ; М=х*f; f ; М=х*f; f 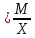
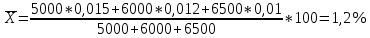
Ответ: Среднемесячный процент брака за второй квартал равен 1,2%
Задача 45
Вычислите коэффициент корреляции на основе следующих данных об объемах выпуска продукции и общих затратах на производство этой продукции:
Завод
|
Объем продукции, т
|
Затраты на производство, тыс. руб.
|
Завод
|
Объем продукции, т
|
Затраты на производство, тыс. руб.
|
1
|
2000
|
400
|
6
|
2800
|
545
|
2
|
2200
|
435
|
7
|
3000
|
582
|
3
|
2400
|
470
|
8
|
3100
|
600
|
4
|
2500
|
490
|
9
|
3150
|
603
|
5
|
2600
|
508
|
10
|
3250
|
617
|
Решение:
Коэффициент корреляции:
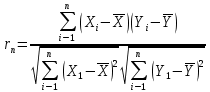 ; ;
Рабочая таблица:
Завод
|
Объем продукции, т
|
Затраты на производство, тыс. руб.
|
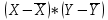
|
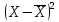
|
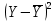
|
1
|
2000
|
400
|
87500
|
490000
|
15625
|
2
|
2200
|
435
|
45000
|
250000
|
8100
|
3
|
2400
|
470
|
16500
|
90000
|
3025
|
4
|
2500
|
490
|
7000
|
40000
|
1225
|
5
|
2600
|
508
|
1700
|
10000
|
289
|
6
|
2800
|
545
|
2000
|
10000
|
400
|
7
|
3000
|
582
|
17100
|
90000
|
3249
|
8
|
3100
|
600
|
30000
|
160000
|
5625
|
9
|
3150
|
603
|
35100
|
202500
|
6084
|
10
|
3250
|
617
|
50600
|
302500
|
8464
|
Среднее
|
2700
|
525
|
|
|
|
Сумма
|
|
|
292500
|
1645000
|
52086
|
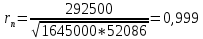
Вывод:
Коэффициент корреляции близок к единице, это говорит о достаточно тесной линейной связи.
Задача 10
Планом промышленного предприятия предусматривалось снижение затрат на 1 руб. товарной продукции на 4 %, фактически затраты возросли на 2%. Вычислите относительную величину выполнения плана.
Решение:
ОВВП= 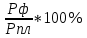
Относительная велич. вып. пл. = 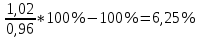
Ответ: План по снижению затрат не выполнен, так как фактический уровень превысил запланированный на 6,25%
|
|
|
 Скачать 31.08 Kb.
Скачать 31.08 Kb.
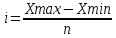 , гдеж X max из X min – максимальное из минимальное значения признака т.е. числовой рабочих, ад n – числовой групп.
, гдеж X max из X min – максимальное из минимальное значения признака т.е. числовой рабочих, ад n – числовой групп. 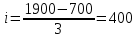 - получили 3 группы:
- получили 3 группы: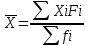
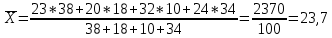
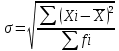
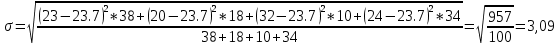
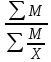 ; М=х*f; f
; М=х*f; f 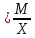
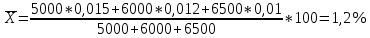
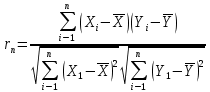 ;
;