Задача 3 Схема расчета надежности резервированного устройства приведена на рис. Рис. 1

• Название: Задача 3 Схема расчета надежности резервированного устройства приведена на рис. Рис. 1
• Дата: 22.04.2023
• Размер: 0.62 Mb.
• Имя файла: 11.doc
• Тип: Задача; #1080521

Задача №3
Схема расчета надежности резервированного устройства приведена на рис. 3.1.



Рис. 3.1

Интенсивности отказов элементов имеют следующие значения:

= 1∙10^-4 1/час, = 1∙10^-4 1/час, = 1∙10^-3 1/час

Предполагается,

1) что последствие отказов элементов отсутствует, то есть элементы работают и отказывают независимо друг от друга,

2) для элементов надежности работы описывается экспоненциальной моделью распределения.

Необходимо найти:

1) вероятность безотказной работы устройства в течение 100 часов;

2) среднюю наработку до первого отказа.
Решение:

1) Определим вероятность безотказной работы устройства в течение 100 часов.

При последовательном соединении,

, (3.1)

где





Подставляя значения в выражение (3.1), получим



= – 3 – 3 + 3 +

+ 9 + 3 – 9 – 9 +

+ 9

Так как , , , то

– 3 – 3 +

+ 3 + 9 + 3 – 9 –

– 9 + 9 = – 3 – 3 +

+ 3 + 9 + 3 – 9 – 9 +

+ 9

При t = 100 получим

0,9048

2) Определим среднюю наработку до первого отказа.

(3.2)

После интегрирования получим

– – + +

+ + – – +

Подставляя в данное выражение для значение интенсивности отказов из условия задачи, получим

– – +

+ + + –

– – + час.

Задача №4
Составить систему уравнений Колмогорова А.Н. для графа состояний резервированной системы, изображенного на рис. 4.1. В данном случае и – работоспособные состояния системы; – неработоспособное состояние; – вероятность нахождения системы в i-ом состоянии; λ – интенсивность отказа; μ – интенсивность восстановления. Найти коэффициент готовности системы , решив полученную систему уравнений.

= 1∙10^-4 1/час; μ = 1∙10^-4 1/час;

Найти предельный коэффициент готовности, применяя теорему А.А. Маркова. Сделать проверку, используя ранее найденный коэффициент готовности . Построить график коэффициента готовности .



Рис. 4.1
Решение:
Составим систему дифференциальных уравнений Колмогорова по следующему правилу:

1) Произ­водная вероятности состояния равна сумме стольких слагаемых, сколько стрелок связано с этим состоянием.

2) Каждое слагаемое равно произведению интенсивности потока собы­тий, переводящего систему по данной стрелке, на вероят­ность того состояния, из которого исходит стрелка.

3) Слага­емое имеет знак минус, если стрелка исходит из данного состояния, а знак плюс – если стрелка направлена в данное состояние.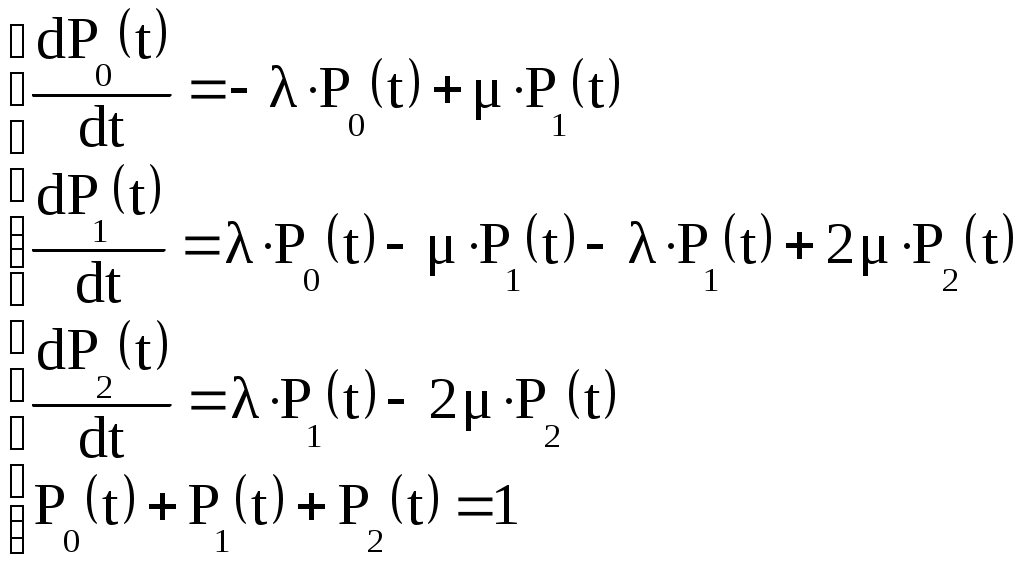

(4.1)

Из последнего уравнения следует, что

(4.2)

и

(4.3)

Исключаем из второго уравнения с помощью (4.2):

(4.4)

Далее находим общее решение системы дифференциальных уравнений

(4.5)

Составим характеристическое уравнение матрицы системы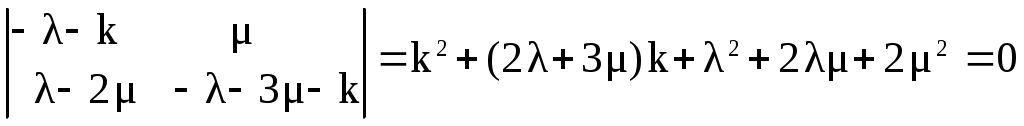



Корни характеристического уравнения





При λ = 1∙10^-4 1/ч; µ = 1∙10^-4 1/ч. Получим







(4.5к₁₂)

Из уравнения получим собственные векторы , соответствующие собственным числам и

,

Следовательно, общее решение однородной части системы (4.5) имеет вид



Частное решение системы (4.5) найдем в виде



После подстановки в систему (4.5) получим



Из второго уравнения получим







Следовательно,



Общее решение системы (4.5) имеет вид

(4.6)

В начальный момент времени система находится в работоспособном состоянии , поэтому

(4.7)

Из (4.6) после подстановки начальных условий (4.7) следует





Вычтем из 2-го уравнения 1-е уравнение умноженное на . Первое уравнение разделим на .

(4.7а)







(4.7б)

Следовательно, после сложения (4.7а), (4.7б) и вычитания после преобразований получим

(4.7в)

(4.7г)

Найдем коэффициент готовности из (4.6): = = (4.8)

После подстановки в (4.8) интенсивностей из условия задачи

λ = 1∙10^-4 1/ч; µ = 1∙10^-4 1/ч.

с учетом (4.7в), (4.7г) и (4.5к₁₂) получим





Построим график коэффициента готовности (рис. 4.2).



Рис. 4.2

Для частичной проверки решений системы дифференциальных уравнений (4.1) заметим, что при t → + ∞ справедлива пре­дельная теорема А.А. Маркова: если все интенсивности по­токов событий постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое за конечное число шагов, то предельные вероятности состоя­ний существуют и не зависят от начального состояния си­стемы.

В соответствии с теоремой А.А. Маркова:

при t → ∞ → , i = 0, 1, 2.

Следовательно, производные

→ 0 , i = 0, 1, 2 при t → ∞,

и система дифференциальных уравнений (4.1) превращается в однородную систему линейных алгебраи­ческих уравнений с нормировочным уравнением:

(4.9)

Ее решение:

(4.10)

Эти же результаты получаем из (4.6) при t → + ∞: корни характеристического уравнения при λ = 1∙10^-4 1/ч; µ = 1∙10^-4 1/ч. отрицательны:





и поэтому все экспоненты в (4.6) при t → + ∞ стремятся к 0, следовательно, пределы дают (4.10).